CONICHE DAL PUNTO DI VISTA ANALITICO

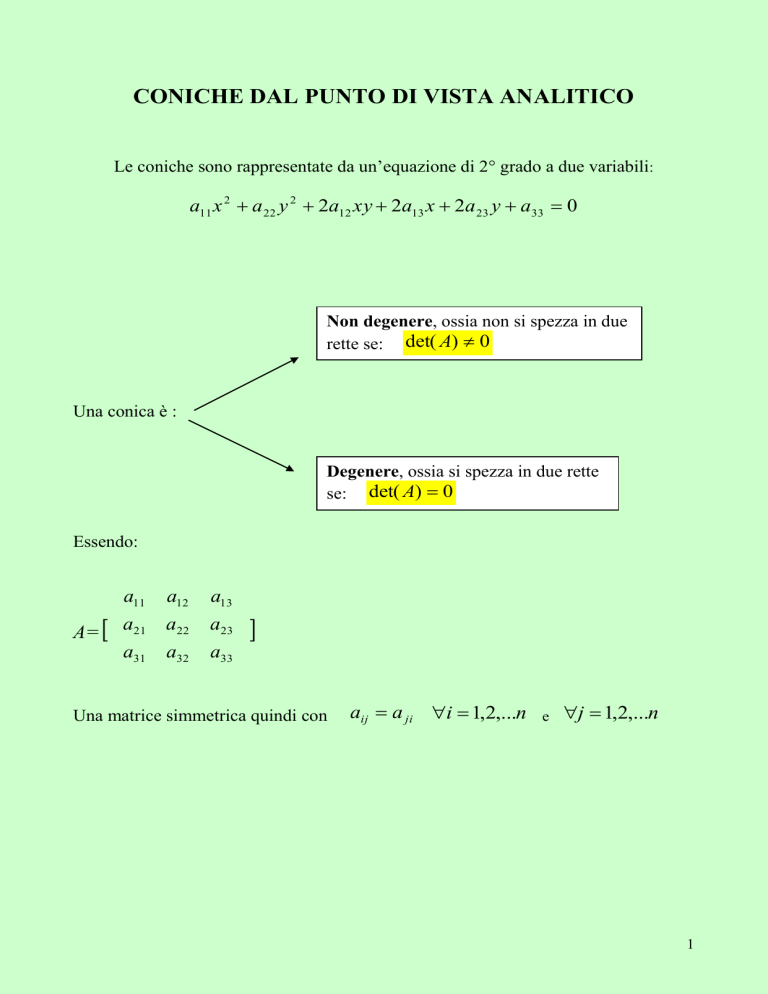
CONICHE DAL PUNTO DI VISTA ANALITICO
Le coniche sono rappresentate da un’equazione di 2° grado a due variabili:
a11 x 2  a 22 y 2  2a12 xy  2a13 x  2a 23 y  a33  0
Non degenere, ossia non si spezza in due
rette se: det( A)  0
Una conica è :
Degenere, ossia si spezza in due rette
se: det( A)  0
Essendo:
a11
a12
a13
A=  a21 a22
a31 a32
a23

a33
Una matrice simmetrica quindi con
aij  a ji i  1,2,...n
e
j  1,2,...n
1
Consideriamo il caso di un conica non degenere ( det( A)  0 ):
Dal determinante:
A33=
a11
a12
a 21
a 22
Abbiamo:
• Se A33 >0,
la conica è un ellisse.
• Se A33 =0,
la conica è una parabola.
• Se A33 <0,
la conica è un’ iperbole.
Esempio
Data l’equazione: 3x  3 y  4 xy  6 x  8 y  1  0
Determinare se è una conica non degenere o degenere e nel caso di una conica non
degenere stabilire la tipologia di conica.
2
2
Svolgimento:
Calcoliamo il determinante :
3 2 3
Det(A)=
2 3 4
= 3  (13)  2  (10)  3  (1)  22  0
3 4 1
Quindi la conica è non degenere.
2
Determiniamo ora la tipologia:
Calcoliamo il determinante:
3 2
A33=
2 3
= 3 3  2  2  5  0
Quindi la conica considerata è un’ellisse.
3