Soluzioni esame Fisica dei beni culturali 20 gennaio 2005-01-25
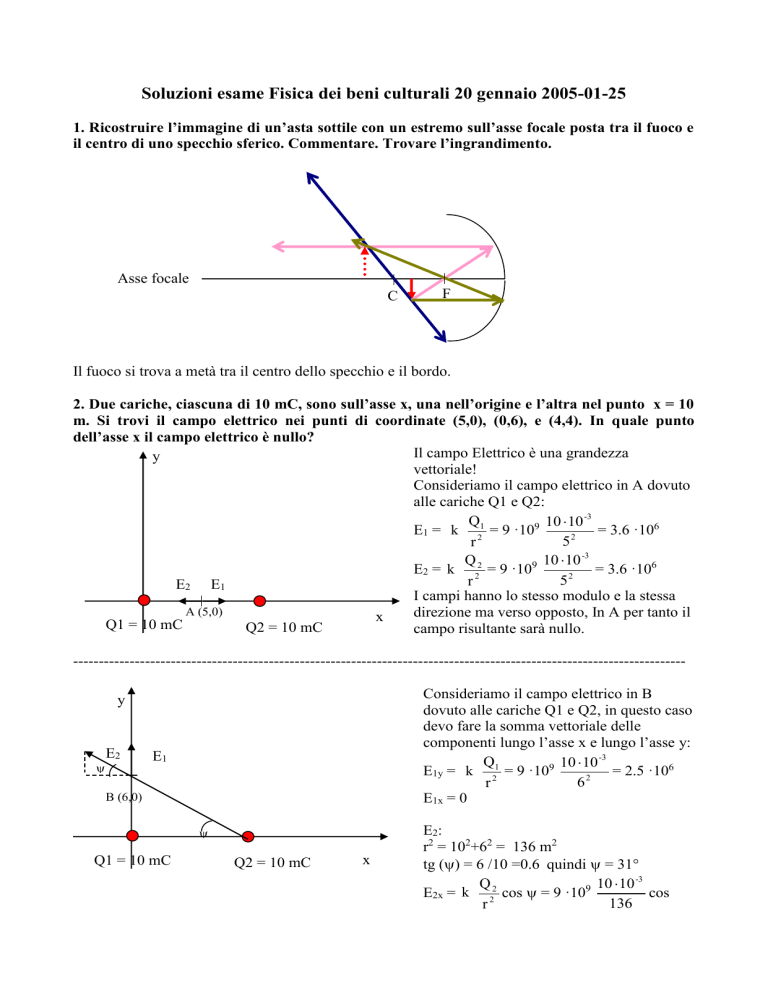
1. Ricostruire l’immagine di un’asta sottile con un estremo sull’asse focale posta tra il fuoco e
il centro di uno specchio sferico. Commentare. Trovare l’ingrandimento.
Asse focale
C
F
Il fuoco si trova a metà tra il centro dello specchio e il bordo.
2. Due cariche, ciascuna di 10 mC, sono sull’asse x, una nell’origine e l’altra nel punto x = 10
m. Si trovi il campo elettrico nei punti di coordinate (5,0), (0,6), e (4,4). In quale punto
dell’asse x il campo elettrico è nullo?
Il campo Elettrico è una grandezza
y
vettoriale!
Consideriamo il campo elettrico in A dovuto
alle cariche Q1 e Q2:
Q
10 10 -3
E1 = k 21 = 9 ·109
= 3.6 ·106
52
r
Q
10 10 -3
E2 = k 22 = 9 ·109
= 3.6 ·106
2
5
r
E2 E1
I campi hanno lo stesso modulo e la stessa
A (5,0)
direzione ma verso opposto, In A per tanto il
x
Q1 = 10 mC
Q2 = 10 mC
campo risultante sarà nullo.
----------------------------------------------------------------------------------------------------------------------Consideriamo il campo elettrico in B
dovuto alle cariche Q1 e Q2, in questo caso
devo fare la somma vettoriale delle
componenti lungo l’asse x e lungo l’asse y:
Q
10 10 -3
E1y = k 21 = 9 ·109
= 2.5 ·106
62
r
E1x = 0
y
E2
E1
B (6,0)
Q1 = 10 mC
Q2 = 10 mC
x
E2:
r2 = 102+62 = 136 m2
tg (= 6 /10 =0.6 quindi = 31°
Q
10 10 -3
E2x = k 22 cos = 9 ·109
cos
136
r
31° = 5.7 ·105 il verso è negativo!
Q
10 10 -3
E2y = k 22 sen = 9 ·109
sen 31° = 3.4 ·105 il verso è y positivo!
136
r
Sommo le componenti su x e su y.
Extot = 0 - 5.7 ·105 = - 5.7 ·105 N/C
Eyot = 2.5 ·106 + 3.4 ·105 = 2.8 ·106 N/C
Erisultante = E xtot E ytot = 2.86 ·106 N/C
2
2
Direzione: tg (’= tg(Eytot/Extot) = tg[(2.84 ·106)/( - 5.7 ·105)] = -78.65 ° ovvero 101.3° dall’asse
delle x.
----------------------------------------------------------------------------------------------------------------------y
E2
E1
(4,4)
Q1 = 10 mC
E1y = k
Q2 = 10 mC
x
Consideriamo il campo elettrico in C
dovuto alle cariche Q1 e Q2, come nel caso
precedente devo fare la somma vettoriale
delle componenti lungo l’asse x e lungo
l’asse y:
E1:
r2 = 42+42 = 32 m2
tg (= 4 /4 =1 quindi = 45°
-3
Q1
9 10 10
k
E1x =
cos = 9 ·10
cos45°
32
r2
E1x = 1.99 ·106 il verso è positivo!
-3
Q1
9 10 10
sen
=
9
·10
sen 45° = 1.99·106 il verso è y positivo!
2
32
r
E2 :
r2 = 62+42 = 52 m2
tg (’= 4 /6 =0.67 quindi ’ = 33.7°
Q
10 10 -3
E2x = k 22 cos ’ = 9 ·109
cos 33.7° = 1.44 ·106 il verso è x negativo!
52
r
-3
Q2
9 10 10
E2y = k 2 sen ’ = 9 ·10
sen 33.7° = 9.60·105 il verso è y positivo!
52
r
Sommo le componenti su x e su y.
Extot = 1.99 ·106 - 1.44 ·106 = 5.50 ·105 N/C
Eyot = 1.99·106 + 9.60 ·105 = 2.95 ·106 N/C
Erisultante = E xtot E ytot = 3.00 ·106 N/C
2
2
Direzione: tg (’= tg(Eytot/Extot) = tg[(2.95 ·106)/( 5.50 ·105)] = 79.4 ° dall’asse delle x.
Il campo elettrico si annulla sull’asse x in (5,0).
3. Un campo magnetico uniforme di modulo 0.5 T è orientato nella direzione x positiva. Si
trovi la forza che agisce su una particella carica di +3.0 nC, se la sua velocità è (a) 200 km/s
nella direzione x positiva, (b) 100 km/h nella direzione z negativa e (c) 300 km/s nel piano yz,
verso l’alto. Lungo una retta che forma un angolo di 60° con l’asse z.
La forza F è definita da:
F = q · v · B · sendove è l’angolo tra il campo magnetico e la velocità della carica.
y
(a) v = 200 km/s = 2 ·105 m/s
=0
F=0
v (c)
v (b)
v (a)
x
B
z
(b) v = 100 km/h = 27.8 m/s
= 90
F = 3 · 10-9 · 27.8 · 0.5 · 1 = 4.2 10 –8 N
(c) v = 300 km/s = 3 ·105 m/s
= 90 la velocità si trova sul piano yz che è ortogonale all’asse x , anche in questo caso
l’angolo tra il campo e la velocità sarà pari a 90°
F = 3 · 10-9 · 3 ·105 · 0.5 · 1 = 4.5 10 –4 N
4. Un proiettile di massa 10 grammi con velocità v0 =10 km/h urta in modo completamente
anelastico un altro corpo di massa 400 grammi che ha velocità iniziale v 1 = 20 km/h nella
stessa direzione dell’altro. Con che velocità si muove il corpo dopo l’urto?
Applico la conservazione della quantità di moto:
m0 · v0 + m1 · v1 = (m0 + m1) · vf
vf = (10 · 10 + 400 · 20)/410 = 19.76 km/h
5. La posizione di una particella è data da: y = (6 cm) · cos (5t). Quali sono (a) la frequenza,
(b) il periodo e (c) l’ampiezza del moto? In quale istante dopo t = 0, la particella è nella sua
posizione di equilibrio? In che direzione si sta movendo in quell’istante?
(a) y = A cos (· t)
= 2 , la frequenza = / (2 ) = 5/ (2 ) = 0.8 Hz
(b) T = 1/ T = 1.25 s
(c) A = 6 cm
Nella condizione di equilibrio y = 0,
0 = (6 cm) · cos (5t); cos(5t) = 0 ;
5t = /2
t = 7.85 s
Direzione in cui si sta muovendo in quell’istante : v = -5 · (6 cm) · sen (5t); all’istante t = 7.85 s il
sen (5 t) è = 1 la velocità ha verso negativo, quindi la particella si sta movendo nella direzione y,
verso negativo.
6. Un blocco di 5 kg scende da un piano inclinato di 30° alto 1 metro, con attrito. Che velocità
raggiunge al termine del percorso se il coefficiente di attrito è 0.2? Che lavoro ha fatto la forza
di gravità? E quale la forza di attrito?
Fattrito = · mg cos30 = 0.2 · 5 · 9.81 · cos 30 = 8.49 N
L = lunghezza del piano = 1/sen(30) = 2 m
Lattrito = F · L· cos = 8.49 · 2 · (-1) = -17 J
Lgravità = mg · L · cos‘ = 5 · 9.81 · 2 · cos 60 = 49.05 J
1/2 mv2= Lgravità +Lattrito = 49.05 – 17 = 32.05
v = 2 * 32.05 / 5 = 3.58 m/s
7. Un fucile spara una palla di piombo da 10 g con un angolo di 30° rispetto all’orizzontale. A
che altezza massima arriva se la velocità si uscita è di 200 km/h e si trascura l’attrito
dell’aria? Qual è la sua gittata? Qual è la sua energia cinetica quando tocca terra? Quale la
sua energia potenziale alla massima altezza della traiettoria?
vy = -g t + v0y
1
y = - g t2 + v0y t
2
x = v0x t
v0 = 200 km/h = 200/3,6 m/s = 55.5 m/s
v0x = v0 cos = 48.06 m/s;v0y = v0 sen 27.75 m/s
y max si ha quando vy = 0 cioè tmax = v0y /g = 2.8 s
2
2
1 v 0y
1 27.75
y=
=
= 39.24 m
2 g
2
g
G = v0x (2 · tmax) = 48.06 · 2 · 2.8 = 271.9 m
E cinetica = 1/2 m v2 = 1/2 m
v 2x v 2y
vx = 48.06 m/s
vy = -g · 2 · tmax + v0y = -27.75
E = 1/2 · 0.01 (55.5 )2 = 15.4 J
E potenziale = mgh = 0.01· 9.81 · 39.24 = 3,85 J
8. Un’automobile viaggia a 10 km/h all’istante t = 0. Essa accelera in modo costante di 2 m/s 2.
Quale sarà la sua velocità all’istante t1 = 1 s? E all’istante t2 = 2 s? Quanto tempo impiega a
raggiungere v=30 km/h e qual è la distanza percorsa? Disegnare il grafico di v in funzione del
tempo.
1 2
a t + v0 t
2
v0 = 10 km/h = 10/3,6 m/s = 2.78 m/s
a= 2 m/s2
v = a t + v0
x=
v(t1 = 1 s) = 2 · 1 s + 2.78 = 4.78 m/s
v(t1 = 2 s) = 2 · 2 s + 2.78 = 6.78 m/s
tempo che impiega a arrivare a 30 km/h = 8.33 m/s
v = a t + v0
8.33= 2 t +2.78
t = 2.8 s
distanza percorsa
1
x = 2· (2.8)2 + 2.78 · 2.8 = 15.6 m
2
disegnare grafico di v in funzione del tempo (retta crescente con pendenza = 2)












