S_130227-MO

MISURE OTTICHE
mercoledì 27 febbraio 2013
Prof. Cesare Svelto
Tempo a disposizione 2h
2a Prova d’esame AA 2012/2013
Aula T.2.2 ore 13.15
COGNOME: ____________________________ Nome: ________________________
(stampatello)
ELN FIS ATM TEL Matricola e firma __ __ __ __ __ __ ___________________ (firma leggibile)
Esercizi svolti (almeno parzialmente)
1 2 3 4
PUNTEGGI:
(9+8+9+7=33 p)
N.B. È richiesto di spuntare tutti i sottopunti cui si è almeno parzialmente risposto [e.g. 1a), 1c), 1d) etc.].
Occorre svolgere tutti gli esercizi, almeno parzialmente, per poter consegnare il compito.
SOLUZIONI
(40 min)
Esercizio 1
(svolgere su questo foglio e sul retro)
1) Un sistema ottico di canalizzazione marina è costituito da un laser a He-Ne il cui fascio d’uscita, con
divergenza 10 mrad (semiangolo di divergenza), è periodicamente commutato su due posizioni angolari di
lancio distanziate tra loro di 0.6 gradi. Il fascio è tenuto per 0.75 s in una posizione e per 0.25 s nell’altra.
L’intensità ottica trasmessa è per ipotesi uniforme all’interno della superficie illuminata.
1a) Dopo avere illustrato brevemente il principio di funzionamento di questo strumento di guida
optoelettronico, si disegnino i tre possibili andamenti nel tempo delle forme d’onda fotorivelate su una
barca in avvicinamento alla riva e quando all’interno del canale ottico marino.
1b) Quanto vale la frequenza del segnale fotorivelato nei tre casi considerati? Quanto sono estese le tre zone
a differente modulazione di luce se la barca si trova a 400 m dalla riva? In che rapporti stanno tra loro le
tre intensità medie della luce fotorivelata?
1c) Se la potenza del laser è di 50 mW e l’ottica di raccolta ha diametro 20 cm e impiega un fotorivelatore al
silicio, si dimensioni il guadagno a transimpedenza per avere segnali d’uscita non inferiori a 1 V (in presenza
di luce) su una distanza di misura di 1 km. Si faccia una ipotesi semplificativa di intensità uniforme.
1d) Se l’intensità luminosa della macchia corrispondente all’immagine del laser è confrontabile, o addirittura
inferiore, rispetto al livello della luce ambiente raccolta sul fotodiodo, come si potrebbe effettuare la
misura anche in orari diurni? Si commentino brevemente le caratteristiche di queste tecniche di misura
che di fatto migliorano il rapporto segnale/disturbo sul segnale ottico.
A riva è posizionato anche un faro, come mostrato in Figura, e sulla barca si usa un rivelatore a
4 quadranti per misurare la distanza dal faro rivelando l’angolo di elevazione sotto il quale è visto il faro dalla
barca. Il rivelatore a 4 quadranti ha un diametro D4Q=2 cm e la macchia luminosa del faro, raccolta sulla
barca attraverso una lente con focale f=200 mm, ha un diametro =300 m sul rivelatore. La risoluzione
nella misura della posizione verticale della macchia di luce sul 4 quadranti è Ymin=100 m.
1e) Si ricavi l’espressione della sensibilità della deviazione verticale Y osservata sul fotodiodo rispetto alle
variazioni della distanza L tra la barca e il faro e il suo valore quando la barca è a 1 km dal faro.
_______
Pag. 1/9
2
1a) Vedi Lezioni/Lucidi e appunti del Corso.
1b) Zona di sinistra (Left): frequenza fL=1/T=1 Hz; diametro macchia DL2L=8 m e WL=4 m.
Zona centrale (Center): frequenza fC=1/=0 Hz; estensione macchia WCL=4 m.
Zona di destra (Right): frequenza fR=1/T=1 Hz; diametro macchia DR2L=8 m e WR=4 m.
Naturalmente, l’intensità ottica (istantanea, quando “ON”) nelle tre zone è sempre la stessa. L’intensità
media dipende dunque dai duty-cycle diversi nelle tre zone: 75 % Left; 100 % Center; 25 % Right.
I tre rapporti cercati sono (tra le intensità ottiche medie o le fotocorrenti corrispondenti) sono: IL/IC=3/4;
IR/IC=1/4; IL/IR=3.
2
2
1c) La potenza trasmessa è PT=50 mW.
L’area illuminata dal fascio trasmesso è AT=r2=(L)2=3.14(1010-3103)2=3.14100=314 m2 (per i
conti che seguono non è importante se parte del fascio è intercettato dalla superficie dell’acqua).
La superficie o area di raccolta è AR=D2/4=3.14(0.2)2/4=3.1410-2 m2.
L’intensità ricevuta, nell’ipotesi semplificativa di “macchia uniforme” e attenuazioni trascurabili, vale
IR=IT=PT/AT=(50 mW)/(314 m2)160 µW/m2. La potenza ricevuta è PR=IRAR=5 W, che si poteva anche
calcolare come PR=PT(AR/AT)= PT(DR/DT)2=50 mW(0.2 m/20 m)2=50 mW10-4=5 W.
D’altronde il “rapporto d’area”, tra fascio trasmesso e area del ricevitore, è appunto SR/ST=10-4.
La fototensione rivelata deve essere VR=GIVSiPR=1 V, ad esempio con Si0.6 A/W, e quindi il
guadagno a transimpedenza del fotorivelatore sarà GIV=VR/(SiPR)=(1 V)/(3 µA)3.3105 V/A=330 k.
2
1d) Per discriminare il debole segnale del laser a He-Ne immerso nella luce ambiente di intensità più elevata,
si potrebbe dotare l’ottica di raccolta di un filtro interferenziale a banda stretta centrato a 633 nm. Oppure, si
potrebbe imprimere una modulazione in AC al segnale laser trasmesso e rivelare in AC il segnale di
fototensione corrispondentemente rivelato (la luce di fondo è inerentemente in DC e viene dunque rigettata).
Entrambe le tecniche proposte, che si basano su un filtraggio spettrale (ottico ed elettrico,
rispettivamente) potrebbero consentire agevolmente un significativo incremento del rapporto segnale/disturbo
ovvero luce laser/ambiente. inoltre, le due tecniche potrebbero anche essere impiegate contemporaneamente.
2
1e) Come equazione del sistema (telemetro) abbiamo:
Y H  h 

 tan    se  <<1
f
L
La sensibilità è definita come il rapporto tra la variazione della grandezza d’uscita e la corrispondente
variazione della grandezza d’ingresso. Nel caso considerato, l’ingresso e la distanza L e l’uscita è la
deflessione Y sul fotorivelatore (v. anche Fig. al punto 1e)). La sensibilità cercata è dunque:
H  h 
Y Y
S

f
L L
L2
Si osserva che S<0 e infatti per L che aumenta  e Y diminuiscono.
Volendo calcolare il valore di sensibilità quando la barca è a 1 km dal faro, dalla espressione precedente si
ottiene S1km=-0.210/(103)2=210-6 m/m=2 mm.
_______
Pag. 2/9
(25 min)
Esercizio 2
(svolgere su questo foglio e sul retro)
2) Un telemetro laser a onda continua (fmod=199 kHz) viene impiegato per misurare le dimensioni di una
galleria autostradale (altezza, lunghezza, e larghezza).
2a) Quale è la dimensione massima misurabile (prima di superare il range di non-ambiguità del telemetro)?
2b) Se la misura di sfasamento tra il fascio laser lanciato e quello ritornato dal bersaglio risolve 5 mrad,
quanto vale la risoluzione L sulla misura di distanza? Come dipende la risoluzione relativa dalla distanza?
2c) Se le dimensioni della galleria sono H=4 m, L=500 m; W=10 m, quanto valgono in gradi gli sfasamenti
corrispondentemente misurati: H, L e W?
2d) Eseguendo la misura della lunghezza H con un telemetro pulsato (laser a Nd:YAG in Q-switching
p10 ns) quanto varrà il tempo di volo rivelato (round-trip)? Con quale risoluzione temporale, T,
occorrerebbe misurare il ritardo tra l’impulso lanciato e quello di ritorno per avere prestazioni confrontabili
con il caso del telemetro a onda continua?
2e) Come si confronta T con la durata dell’impulso e con quale altro tipo di laser si potrebbero mitigare le
problematiche di questa misura impulsata?
_______
Pag. 3/9
22a) Il
non-ambiguity range del telemetro, Lna, è legato al tempo di non ambiguità, Tna, dalla relazione
2Lna=cTna
Inoltre da 2fmodTna = 2 si ricava Tna=1/fmod50 s.
c 1
Quindi Lna=
=1.5108 (m/s) / 199105 Hz750 m.
2 f mod
22b) La
misura di distanza, entro il non-ambiguity range, si ottiene dalla relazione
c 1
 =SL- 120 m/rad×
L=
2 2f mod
dove SL- è la sensibilità della misura, vista come dipendenza della lunghezza L dalla fase .
Dunque la risoluzione assoluta è
c 1
 =120 m/rad×510-3 rad=0.6 m (=cost.)
L=
2 2f mod
Con una risoluzione relativa L/LL-1 che dipende dalla distanza L misurata e di fatto migliora
all’aumentare della distanza.
22c) I
tre sfasamenti cercati sono:
H=H/SL-=(4 m)/(120 m/rad)33 mrad1.9 °2 °
L=H/SL-=(500 m)/(120 m/rad)4.17 rad239 °240 °
W=H/SL-=(10 m)/(120 m/rad)83 mrad4.8 °5 °
tempo di volo (round-trip) è TH=2H/c=27 ns°30 ns. Nella misura per tempo di volo, L=(c/2)×T,
per avere L=0.6 m (come per il telemetro a onda continua) deve essere T=(2/c)×L=4 ns. Impiegando il
laser in Q-switching indicato nell’esercizio, la risoluzione temporale richiesta (T=4 ns) risulta lievemente
più piccola della durata dell’impulso ottico (p=10 ns): si ha infatti T/p0.5. La misura in queste
condizioni è piuttosto disagevole e può comportare errori significativi.
22d) Il
22e) Per
mitigare questo problema converrebbe impiegare impulsi di durata più breve. Ad esempio,
utilizzando una sorgente laser in mode-locking con p,ml10 ps, si ottiene T/p,ml=400 per cui la misura
diviene più agevole e anzi si può pensare di avere risoluzioni L anche dell’ordine del centimetro (risolvendo
T=66 ps7p,ml).
_______
Pag. 4/9
(30 min)
Esercizio 3
(svolgere su questo foglio e sul retro)
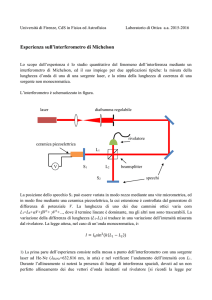
3) In figura è riportato lo schema di un interferometro di Michelson. La sorgente è un laser DFB che emette
una potenza P0 = 10 mW, alla lunghezza d’onda  = 1550 nm. Grazie alla presenza di un isolatore ottico
(che evita le retro riflessioni nel laser), la larghezza di riga del laser DFB è pari a 300 kHz. Il segnale
interferometrico è rivelato per mezzo di un fotodiodo con responsività  pari a 0.5 A/W. Il bersaglio è
costituito da un altoparlante eccitato alla frequenza fa = 100 Hz da una sinusoide di ampiezza di picco Va =
10 V (la sensibilità, in spostamento, dell’altoparlante è Ka = 2.635 m/V). Lm = 1 m e Lr = 0.5 m:
l’interferometro è dunque sbilanciato.
3a) Si calcolino i valori di potenza ottica massima, Pmax, e minima, Pmin, incidenti sul fotodiodo.
3b) Il segnale di fotocorrente generato dal fotodiodo è amplificato per mezzo di amplificatore a transimpedenza, con resistenza di reazione R = 10 kSi ricavi l’espressione analitica della fototensione V in
funzione del tempo, ricavando in particolare i valori Vmax e Vmin.
3c) Ipotizzando di eseguire la misura di spostamento per conteggio di frange, quale sarà la risoluzione
dell’interferometro proposto? Si ricavi il valore dello sfasamento tra segnale di riferimento e di misura per
un’escursione completa dell’altoparlante. A quante frange interferometriche corrisponde tale sfasamento?
Qual è la banda B che deve essere garantita per una corretta misura della vibrazione dell’altoparlante?
3d) Nel caso si voglia utilizzare l’interferometro in esame per effettuare misure di vibrazioni picco-picco da
1 nm a 100 nm, come bisogna modificare lo schema di lettura dell’interferometro? In queste condizioni da
cosa è dettata la risoluzione dell’interferometro? La risoluzione può dipendere dal valore di Lm e Lr? (Per
rispondere si ipotizzi una visibilità delle frange unitaria, una banda di osservazione di 15 kHz, e una corrente
media fotorivelata pari a I0 = 1.5 mA)
_______
Pag. 5/9
La potenza riflessa dall’altoparlante è Pa = (P0/2)  (5/100) = 0.25 mW e quella riflessa dallo specchio è Ps =
(P0/2)  (90/100) = 4.5 mW. Le due potenze ottiche che si ricombinano sul fotodiodo sono P1 = Pa/2 = 0.125 mW e
P2 = Ps/2 = 2.25 mW. Note P1 e P2, le potenze ottiche massima e minima del battimento sul fotodiodo sono:
Pmax = P1 + P2 + 2 (P1P2)1/2≈ 3.435 mW;
Pmin = P1 + P2 – 2 (P1P2)1/2 ≈ 1.314 mW.
23a)
23b)
La fototensione V(t) è legata alla potenza ottica secondo la seguente relazione:
V(t) = R I(t) = R  P(t).
La potenza ottica P(t) varia nel tempo a causa dell’interferenza dei segnali P1 e P2 con la legge seguente: P(t)
= P1 + P2 + 2 (P1P2)1/2 cos [2k(Lm + s - Lr)], con k numero d’onda pari a 2/, s spostamento temporale
dell’altoparlante pari a s0cos(2fat), ed s0 = Va Ka = 26.35 m.
Riassumendo:
V(t) = R   P1 + P2 + 2 (P1P2)1/2 cos [ 4/0 s0cos(2fat) ] ;
Vmax = R  Pmax = 17.175 V;
Vfmin = R  Pmin = 6.585 V.
33c)
Trattandosi di un interferometro di Michelson classico e non essendo specificato nessun particolare
metodo di elaborazione del segnale Vf(t), la risoluzione dell’interferometro è pari a 0/2 = 775 nm.
Durante un’escursione completa dell’altoparlante (s = 2s0 = 52.7 m), lo sfasamento complessivamente
accumulato fra segnale di riferimento e di misura è pari a:
 t = 2 k 2s0 = 8s0/0 = 427.04 rad.
Tale sfasamento corrisponde a un numero di frange interferometriche pari a:
NF =  t / 2 = 68.
Allo stesso risultato si arriva dividendo lo spostamento complessivo dell’altoparlante, pari a 2s0, per lo
spostamento che genera una frangia interferometrica nel segnale V(t), pari a 0/2: NF=(2s0)/(0/2)=68.
La banda di misura dell’interferometro deve garantire la risoluzione di 68 frange interferometriche in un tempo Tm
= Ta / 2 = 1 / 2fa = 5 ms. La banda dunque deve essere maggiore del valore minimo Bmin = (NF / Tm) = 13.6 kHz e
magari si può operare con B=10Bmin=136 kHz150 kHz.
Quando si desidera effettuare misure di spostamenti/vibrazioni molto inferiori a 0/2, bisogna apportare
alcune modifiche allo schema analizzato in precedenza.
Dal punto di vista dell’elaborazione del segnale è necessario mantenere l’interferometro in quadratura
(aggancio a mezza frangia) per poter sfruttare il tratto lineare della caratteristica di trasferimento
fase/spostamento – fototensione V(t).
In queste condizioni la risoluzione dell’interferometro/vibrometro è data dalla NED (Noise Equivalent
Displacement).
I contributi alla NED sono dati dal rumore shot legato al processo di rivelazione del segnale ottico e dalla
larghezza di riga finita del laser e dalla sua interazione con lo sbilanciamento dell’interferometro.
La NED legata alla larghezza di riga non nulla della sorgente laser è data dalla relazione:
NEDriga = ( Lm - Lr )(Δ/0) = 0.5 m  (300 kHz/200 THz)=0.775 nm=775 pm, dove 0 = c / 0.
La NED legata al rumore shot di rivelazione è data dalla relazione:
NEDshot = (0/2)(qB/2I0)1/2, dove q = 1.6 10-19 C è la carica dell’elettrone, B = 15 kHz, e I0 = 1.5 mA.
Il limite di risoluzione legato alla NEDriga è in questo caso, e anche generalmente, molto maggiore del limite
NEDshot e risulta il termine dominante quando l’interferometro è sbilanciato. Per effettuare la misura indicata
( è quindi opportuno lavorare in condizioni d’interferometro bilanciato ( Lm = Lr ) in modo da annullare la
NEDriga.
Se riuscissimo a bilanciare l’interferometro e a lavorare agganciati a mezza frangia, la risoluzione limite
dell’interferometro diventerebbe NEDshot = 2.2 10-13 m = 0.22 pm.
33d)
_______
Pag. 6/9
(25 min)
Esercizio 4
(svolgere su questo foglio e sul retro)
4a) Si descriva, aiutandosi con un disegno dello strumento, il funzionamento di un sistema di misura LDV.
4b) Facendo riferimento a un disegno dettagliato della zona di interferenza, si ricavi l’espressione della distanza
tra le frange interferometriche e quella della frequenza osservata quando si misura una velocità v.
Un sistema LDV è impiegato per misurare la velocità di uscita dei gas combusti in un turbojet a reazione.
Il laser utilizzato è un He-Ne nel rosso e il fascio “splittato” viene fatto incidere sulla lente di focalizzazione
(f=800 mm) a una distanza di 3 cm dall’asse ottico. Nella zona di fuoco/interazione le due macchie laser
hanno raggio uguale e paria a w0=4 mm.
4c) Se la velocità v può variare da 50 m/s fino a 1400 m/s, quali frequenze si devono poter rivelare all’uscita
del fotodiodo di rivelazione?
4d) Misurando il segnale fotorivelato con un’analisi spettrale a FFT, quale velocità di campionamento
occorre rispettare? Quale convertitore A/D conviene o si deve impiegare? Quali possono essere le
richieste sulla risoluzione del convertitore A/D usato per la misura? Si motivino le risposte date.
4e) Quale strumento di misura si potrebbe impiegare per effettuare convenientemente la misura del punto
4d)? Quali caratteristiche minime deve avere lo strumento?
_______
Pag. 7/9
24a) Vedi
Lezioni/Lucidi e appunti del Corso.
24b) Vedi
Lezioni/Lucidi e appunti del Corso.
La distanza tra due frange d’interferenza (tra due massimi o due minimi di luce) è D=/(2sin).
Il periodo di attraversamento tra due frange adiacenti è T=D/ v=/(2vsin) e la corrispondente frequenza
è f=1/T=(2vsin)/v.
24c) =arctg(30
mm)/(800 mm)37.5 mrad=2.15 ° e per l’He-Ne nel rosso =632.8 nm633 nm.
D=/(2sin)8.4 m.
fmin=(2vminsin)/=5.9 MHz6 MHz e fmax=(2vmaxsin)/=165.8 MHz166 MHz.
24d) Per
ottenere un corretto campionamento dei segnali di luce dopo l’attraversamento delle frange
(emissione di luce quasi-sinusoidale), occorre campionare almeno al doppio della massima frequenza di
attraversamento (teorema di Shannon): pertanto, fsample ≥ fmax=332 MSa/s e si può scegliere fsample=350 MSa/s
o anche fsample=500 MSa/s.
La velocità richiesta per l’acquisizione impone l’uso di un convertitore A/D di tipo flash e dunque una
risoluzione di misura fissata a n=8 bit e N=256 livelli. Volendo l’analisi spettrale a FFT rivelare a quale
frequenza si colloca il segnale misurato, e non essendo importante discriminare con accuratezza i livelli di
ampiezza/potenza nello spettro calcolato, una risoluzione anche a soli 8 bit dovrebbe essere più che sufficiente.
24e) Uno
strumento che impiega un convertitore A/D a 8 bit ed è in grado di eseguire il calcolo di uno spettro
FFT del segnale misurato è l’oscilloscopio digitale, che in questo caso deve avere una banda passante di
almeno 200 MHz (una lieve attenuazione e sfasamento sul segnale misurato è accettabile dato che interessa
solo il valore della frequenza spettrale) e ad esempio un convertitore da 500 MSa/s (sarà più facile che il
convertitore A/D abbia addirittura una velocità di 1 GSa/s). Una scheda di acquisizione dati, o altro
hardware dedicato, andrebbero altrettanto bene pur di rispettare i 200 MHz di banda analogica e almeno
350 MSa/s come velocità di campionamento.
Con le frequenze sotto misura è anche possibile impiegare un analizzatore di spettro a eterodina
(analogico) in grado di risolvere con buona risoluzione i picchi di frequenza/velocità e di mostrare al
contempo l’intero spettro continuo nel quale l’asse orizzontale di frequenza del segnale elettronico
corrisponde a un asse di velocità misurata e l’asse verticale delle potenze/ampiezze corrisponde alla densità
di probabilità di avere particelle in moto nel fluido con una data velocità.
_______
Pag. 8/9
Foglio extra per soluzioni “lunghe”
(svolgere su questo foglio e sul retro)
_______
Pag. 9/9