Esercizi02
Variabili aleatorie unidimensionali,
media, varianza, mediana, moda,
quantili.
Richiami di teoria 1: media e varianza di una v.a.
Media di una v.a.: sia X una v.a. (dotata di punti di massa xj e legge
pX(x) se discreta, di funzione di densità fX(x) se continua). La media E[X]
è data da:
E [ X ]=μ X = ∑ x j p X x j , se X è discreta,
j
∞
E [ X ]=μ X = ∫ xf X x dx, se X è continua
−∞
a patto che queste quantità esistano;
Varianza di una v.a.: sia X una v.a. di media X; la varianza di X, indicata
con 2X, o Var(X) è data da:
σ 2 = ∑ x j− μ X
X
σ =∫
2
pX x j ,
se X è discreta,
j
∞
2X
−∞
x− μ X
2
f
X
se queste quantità sono definite.
ottobre 2008
x dx ,
se X è continua
Richiami di teoria 2: mediana, quantili e percentili
Data la funzione di ripartizione FX di una v.a. X la mediana è il minimo
valore m tale che
F X m =P X ≤ m ≥ 1/2 cioè m=inf {ξ:F X ξ ≥ 1/2 }
Analogamente si dice quantile q-esimo (0<q<1) della FX di una v.a. X il
minimo valore q tale che
F X x =P X ≤ x =q
x q = inf {x:F X x =q }
Se q viene espresso con una percentuale invece che con un numero q,
viene definito 100q-esimo percentile.
ottobre 2008
Esercizio 1: testo
Quattro autobus portano 148 studenti allo stadio di football; gli autobus
portano rispettivamente 40, 33, 25 e 50 studenti. Scegliamo a caso uno
degli studenti, e denotiamo con X il numero degli studenti che hanno
viaggiato sull’autobus dello studente scelto a caso. Scegliamo a caso
ora uno dei conducenti dei bus e denotiamo con Y il numero degli
studenti che hanno viaggiato sul suo autobus.
n Quale tra E[X] ed E[Y] pensate sia più grande? Perché?
n Si calcolino E[X] ed E[Y]
ottobre 2008
Esercizio 1- Soluzione
n
n
A voi: proposte?
Che valori può assumere la variabile X?
40
33
X=
25
50
p= 40148
p= 33148
p= 25148
p= 50148
{ }
Quindi siamo capaci di calcolare la sua media:
40
33
25
50
E X = 40
33
25
50
≃ 39. 284
148
148
148
148
Un discorso analogo vale per Y:
40
33
Y=
25
50
p=14
p=14
p=14
p=14
{ }
ottobre 2008
Esercizio 1- Soluzione
Sono quindi in grado di calcolare anche la media di Y:
E Y = 40
1
4
33
1
1
1 148
25
50 =
= 37 .
4
4
4
4
Le due variabili assumono valori identici ma con differenti probabilità.
ottobre 2008
Esercizio 2: testo e soluzione del punti 1
Sia X una variabile aleatoria tale per cui E(X)=1, e Var(X)=5.
Si calcoli:
E [(2+X)2];
Var(4+3X);
SVOLGIMENTO
2
2
Calcoliamo la media:
E [ 2+X ]=E 4 4X+X = 4 4E X +E X 2
Ci manca E[X2], ma possiamo ottenerlo con la formula
2
Var X =E X − E X ⇒E X 2 = 5 1= 6
2
Si ottiene perciò
E [ 2 +X
ottobre 2008
2
]= 4
4⋅ 1
6= 14
Esercizio 2: testo e soluzione del punto2
E la varianza, sarà
Var 4 3X = 0+Var 3X = 9Var X = 45.
ottobre 2008
Esercizio 3: testo
Da un mazzo di 52 carte se ne estraggono 5. Sia X la v.a. che conta il
numero di assi contenuti nelle 5 carte. Dire quali sono le determinazioni
di X ed indicare la sua funzione di densità discreta.
ottobre 2008
Esercizio 3- Soluzione
Tra le 5 carte pescate si possono presentare 0, 1, 2, 3 oppure 4 assi.
Con quale probabilità?
X=0
p=
X=1
X=2
p=
p=
X=3
X=4
ottobre 2008
4
0
48
5
52
5
4
1
48
4
52
5
4
2
48
3
= 0 . 658 ;
= 0 . 298 ;
= 0 . 0398 ;
52
5
p=0 . 00174 ;
p= 1. 847⋅ 10− 5
Esercizio 3- Soluzione
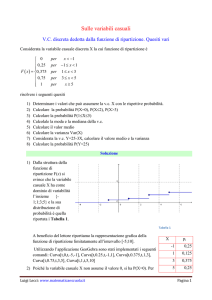
Tali probabilità rappresentano la densità discreta della variabile X. Si possono
allora disegnare i grafici della densità discreta pX(x) e della funzione di
ripartizione FX(x):
ottobre 2008
Esempio
Si tirano due dadi indipendenti e non truccati, e si denota con la lettera X la v.a.
definita dalla loro somma. Ricaviamo la densità discreta di X:
P
P
P
⋯
P
⋯
P
X=2 =P { 1,1 }= 136 ;
X=3 =P { 1,2 , 2,1 }= 236 ;
X=4 =P { 1,3 , 2,2 , 3,1 }= 336 ;
X=7 =P { 1,6 , 2,5 , 3,4 , 4,3 , 5,2 , 6,1 }= 636 ;
X=12 =P { 6,6 }= 136 ;
X assume tutti i valori interi da 2 a 12, con probabilità specificate dalle equazioni
precedenti; poiché 12
X deve necessariamente assumere uno di questi valori,
S=
i=2 {X=i } varrà che
segue che se
P S =P ¿i=212 {X=i } = ∑ P X=i = 1.
ottobre 2008
Esercizio 5: testo e soluzione
2
3
Sia F X t = 3t − 2t I [ 0,1 ] t +I [1,+¥] t
, dove IA(t) è la funzione
indicatrice dell’insieme A, la f.d.r. di una v.a. X :
Considerando che il grafico di FX(t) è il seguente, dire quali delle
seguenti sono vere e quali false:
P X³ 1 = 1
P X≤ 0= 0
P X=12 = 12
P 0≤ X<12 = 0
P − 5≤ X ≤ 8 = 1
ottobre 2008
V
V
F
F
V
Esercizio 6: testo
Una v.a. continua ha densità
f x=
{
kx 0<x< 4
0 altrove
}
Determinare la costante di normalizzazione k, e poi calcolare P X ≤ 2 .
Calcolare inoltre il valore atteso e la mediana di X.
ottobre 2008
Esercizio 6- Soluzione
∞
k deve essere tale che
∫
f x dx=1
perciò
−∞
4
∫
0
x2 4
1
kxdx=k ∣ ∣ = 8k= 1, cioè k= .
2 0
8
Inoltre
2
P X ≤ 2 =∫
0
ottobre 2008
1
1
xdx= .
8
4
Esercizio 6- Soluzione
Calcoliamo il valore atteso:
4
E X =∫
0
1
1 x3 4 8
x xdx= ∣ ∣ = .
8
8 3 0 3
Poiché X è continua, la mediana è il valore m tale che F m = 0.5 .
Per 0 <x<4 si ha:
x
F x =∫
0
1
1
tdt= x 2 ,
8
16
e perciò la mediana deve soddisfare
1 2
F m=
m = 0 .5, da cui m= 8.
16
ottobre 2008
Esercizi per voi
La funzione
{
2
3x
0 <x<1
f x=
0 altrove
}
è una funzione di densità? Se lo è, calcolatene la corrispondente
funzione di ripartizione.
Determinare la mediana ed il terzo quartile delle variabili aleatorie
definite dalle seguenti funzioni di densità:
f x =e− x , x³ 0;
f x = 1, 0≤ x≤ 1.
Determinare il k-esimo quantile mp ( con p=k 100 ) in funzione di p, per
la variabile aleatoria di densità
f x = 2e− 2x , x³ 0.
Sapendo che
E X = 2, E X 2 = 8, calcolare
2
E 2 4X , e E [ X
ottobre 2008
2
2
X+1 ].