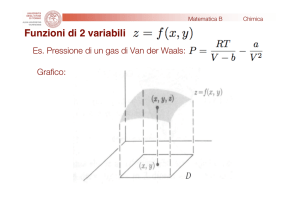
NMR- IMAGING
(2° parte)
“Tecniche chimico-fisiche in ambito sanitario”
Dott.ssa Isabella Nicotera
PRINCIPI DI
IMAGING CON FT
Introduciamo il concetto di una terza categoria di gradienti di campo
magnetico chiamati gradienti di codifica di fase
questi, uniti ai gradienti di selezione della fetta e ai gradienti di codifica
in frequenza, sono al giorno d'oggi usati nell' imaging tomografico MRI
basato sulla Trasformata di Fourier.
Il gradiente di codifica di fase
è un gradiente del campo magnetico B0, ed è usato per impartire al vettore
magnetizzazione trasversale (Mt) un angolo di fase specifico che dipende dalla
localizzazione del vettore
Mt stesso
Gx
δB z
δx
Il gradiente di codifica di fase
Se si immagina di avere tre regioni di spin, e si ruota il vettore di magnetizzazione trasversale
relativo a ciascuno spin lungo l'asse y (slide selection), i tre vettori hanno lo stesso "chemical shift"
e quindi, in un campo magnetico uniforme, avranno la stessa frequenza di Larmor.
Applicando un ulteriore gradiente di campo lungo la direzione x, i tre vettori precedono
lungo la direzione del gradiente a frequenze date dall'equazione:
n = g ( Bo + x Gx) = no + g x Gx
Mentre il gradiente di codifica di fase e' acceso, ciascun vettore di magnetizzazione
trasversale ha la sua propria (unica) frequenza di Larmor.
Questa descrizione della codifica di fase è identica a quella della codifica in frequenza.
Se il gradiente nella direzione x viene spento, il campo magnetico esterno subito da ciascuno
spin è identico, quindi sarà nuovamente identica la frequenza di Larmor di ciascun vettore di
magnetizzazione trasversale.
….ma…
l'angolo della fase di ciascun vettore non è identico
L'angolo della fase è l'angolo che il vettore di magnetizzazione forma con un asse di
riferimento, ad esempio l’asse y, al tempo in cui il gradiente di codifica di fase viene
spento. Ci sono tre angoli della fase distinti in questo esempio. Se si avesse un modo di
misurare la fase dei vettori di rotazione, si potrebbe loro assegnare una posizione lungo
l'asse x.
La procedura introdotta permette di spiegare una semplice sequenza usata per ottenere
immagini tomografiche/volumetriche con l'uso della trasformata di Fourier.
Imaging in trasformata di Fourier
Uno dei migliori modi per capire una sequenza di imaging è esaminare il diagramma temporale della sequenza .
In generale in tali diagrammi vengono riportati la radio-frequenza, i gradienti di campo magnetico ed il segnale in
funzione del tempo.
La più semplice sequenza per imaging con FT contiene un impulso a 90° (RF), un gradiente per la
selezione della fetta (Gs ), un gradiente per la codifica di fase (GФ ), un gradiente per la codifica
in frequenza (Gf ) e un segnale.
Il reale diagramma temporale per questa sequenza e' un po' piu' complicato di quello proposto,
che ne e' una semplificazione per scopi introduttivi.
Gli impulsi relativi ai tre gradienti sono rappresentativi dell'intensità (ampiezza) e della durata
degli stessi.
Vediamoli uno alla volta:
Il primo evento che ha luogo secondo questa sequenza di imaging e' l'attivazione del
gradiente per la selezione della fetta. L'impulso RF per la selezione della fetta e' applicato
nello stesso istante. L'impulso RF per la selezione della fetta e' una "breve e intensa"
cessione di energia con un impulso che ha la forma della funzione sinc.
Al termine dell'impulso di RF, il gradiente per la selezione della fetta viene spento e
viene attivato il gradiente per la
codifica di fase
Una volta che il gradiente per la codifica di fase viene spento, viene acceso il
gradiente per la codifica in frequenza
e viene registrato un segnale (nella forma di un FID).
Il gradiente di selezione della fetta e' sempre applicato perpendicolarmente al piano della
fetta;
Il gradiente di codifica di fase e' applicato lungo uno dei lati del piano dell'immagine
mentre il gradiente di codifica in frequenza e' applicato lungo il rimanente lato del piano
dell'immagine.
La tabella seguente indica le possibili combinazioni dei gradienti di selezione della fetta, di
codifica di fase e di codifica in frequenza.
Gradiente
Piano
immagine
Posizione
fetta
Fase
Frequenza
XY
Z
XoY
YoX
XZ
Y
XoZ
ZoX
YZ
X
YoZ
ZoY
Questa sequenza di impulsi di solito e' ripetuta 128 o 256 volte per raccogliere tutti i dati necessari a
produrre un'immagine.
Il tempo tra le ripetizioni della sequenza e' chiamato il tempo di ripetizione, TR.
Ogni volta che la sequenza viene ripetuta l'intensita' del gradiente di codifica della fase cambia:
viene incrementata con un certo "passo" a partire dal valore minimo fino alla massima ampiezza
del gradiente…..
Perché?
La sequenza può essere descritta secondo la prospettiva macroscopica dei vettori di spin.
Consideriamo un cubo di spin posto in un campo magnetico composto da molti elementi di
volume, ognuno, quindi, col suo proprio vettore di magnetizzazione netta ed applichiamo i
gradienti di selezione della fetta, di codifica di fase e di frequenza, insieme al campo
magnetico B0 applicato lungo la direzione dell'asse z di laboratorio.
Il gradiente di selezione della fetta è diretto lungo lo stesso asse z. Gli impulsi RF faranno
ruotare solamente quei pacchetti di spin nel cubo che soddisfano la condizione di risonanza.
Questi pacchetti di spin sono localizzati, in questo esempio, in un piano xy. La localizzazione
del piano lungo l'asse z rispetto all'isocentro è data da:
Z = n / g Gs
Dove n e' la differenza di frequenza rispetto a no ( i.e. n - no ), Gs è l'intensità del
gradiente di selezione della fetta e g il rapporto giromagnetico
Gli spin localizzati sopra e sotto questo piano non sono interessati dagli impulsi RF; saranno perciò trascurati
Per semplificare il resto della presentazione, si considera solo un sottoinsieme 3x3
dei vettori di magnetizzazione netta.
L'immagine di questi spin in questo piano sarà come schematizzato in figura:
y
x
Una volta ruotati nel piano XY questi vettori possono viaggiare ad una velocità di
precessione uguale alla frequenza di Larmor data dal campo magnetico che ognuno stava
subendo.
Se il campo magnetico è uniforme, ognuna delle nove frequenze di precessione è uguale
(fase e frequenza).
y
x
Nella sequenza per imaging, dopo il gradiente di selezione della fetta e' applicato un
gradiente di codifica di fase
Assumendo che questo sia applicato lungo l'asse x, gli spin a diverse posizioni lungo
l'asse x cominciano a muoversi di moto di precessione a frequenze di Larmor diverse.
y
x
Quando il gradiente di codifica di fase e' spento, i vettori di magnetizzazione netta
ruotano con ugual frequenza ma possiedono fasi diverse.
La fase e' determinata dalla durata e dall'ampiezza degli impulsi del
gradiente di codifica di fase.
y
x
Terminato l'impulso del gradiente di codifica di fase, viene attivato il gradiente di
codifica in frequenza (In questo esempio il gradiente di codifica in frequenza e' nella direzione Y ).
Esso causa una velocità di precessione dei pacchetti di spin dipendente dalla loro localizzazione su
Y: quindi ognuno dei nove vettori di magnetizzazione netta è caratterizzato da un unico
valore di angolo della fase ed un unico valore di frequenza di precessione.
Si è cosi differenziato ogni vettore di magnetizzazione nello spazio del piano XY
y
x
Se avessimo un modo per determinare fase e frequenza del segnale da un vettore di magnetizzazione netta,
potremmo associarlo a uno dei nove elementi.
Una semplice trasformata di Fourier è in grado di far questo per un singolo vettore di magnetizzazione netta
localizzato in qualche punto nello spazio 3x3.
Per esempio, se un singolo vettore fosse localizzato a (X,Y) = 2,2, i suoi FID conterrebbero un’onda
sinusoidale di frequenza 2 e fase 2. Una trasformata di Fourier di questo segnale produrrebbe un picco a
frequenza 2 e fase 2.
y
x
Sfortunatamente una trasformata di Fourier monodimensionale non è in grado di far
questo in una matrice 3x3, quando più di un vettore è localizzato in una differente
posizione lungo la direzione di codifica di fase.
Ci vorrebbe un incremento del gradiente di codifica di fase per ciascuna localizzazione
nella direzione del gradiente di codifica di fase. Il fatto è che avete bisogno di
un’equazione per ogni punto sconosciuto che state cercando di risolvere.
Quindi se ci sono tre localizzazioni lungo la direzione di codifica di fase avremo bisogno di tre
intensità di gradienti di codifica di fase e di tre unici FID.
Se vogliamo risolvere 256 punti nella direzione della codifica di fase avremmo bisogno di 256
differenti intensità di gradiente di codifica di fase e registreremo 256 differenti FID.
Analisi del segnale
Al fine di ottenere un'immagine o mappa di localizzazione degli spin, i FID o i segnali sopra descritti
devono essere trasformati secondo Fourier.
I segnali sono prima trasformati secondo Fourier nella direzione x per estrarre le informazioni
del dominio delle frequenze e, poi,
nella direzione di codifica di fase (-y) per estrarre le informazioni circa la localizzazione nella
direzione di applicazione del gradiente di codifica di fase.
L’NMR Imaging può essere percepito come una forma particolare di spettroscopia multi-dimensionale
dove l’asse di frequenza è convertito in asse spaziale mediante l’applicazione di campi magnetici
disomogenei (un gradiente di campo).
In un campo magnetico dipendente dallo spazio, la frequenza di Larmor dipende dalla
posizione; in questo caso ogni punto lungo l’asse x del campione è caratterizzato da una
differente frequenza di risonanza.
L’intensità totale del segnale è proporzionale al numero di nuclei (densità di spin, ), su
una data frequenza NMR, ed è calcolata mediante l’integrazione, secondo trasformata di
Fourier, della magnetizzazione del campione lungo l’asse x:
FID(t ) ( x) exp[ i γ G x x t ] dx
x
Numero di nuclei che sono locati a x dal centro del gradiente
Analisi del segnale
FID(t ) ρ(x) exp[i γ G x x t ] dx
x
Ponendo Kx = g Gx t e sostituendo si ha:
FID( K x ) ( x) exp[ iK x x]dx
x
Il segnale è la somma dei segnali originati dai singoli nuclei in tutte le posizioni lungo
l’asse x acquisito nel tempo t.
Analisi del segnale
Considerando la raccolta del segnale in presenza dei gradienti di frequenza (gx) e di
fase (gy) (sistema bidimensionale), il segnale risulterà dato da:
FID(t x , G y ) ( x, y ) exp[ igGx xtx ] exp[ igG y yt ]dxdy
x, y
lungo x: accendiamo Gx (costante) e acquisiamo nel tempo tx (variabile)
lungo y: variamo ad ogni step (128 o 256) il gradiente Gy e lo teniamo acceso per un
t costante
FID(t x , G y ) ( x, y ) exp[ ig (Gx xtx G y yt ]dxdy
x, y
Frequency encoding
FID(k x , k y )
x
ik x x
ρ(x,
y)
e
e
y
Phase encoding
ik y y
dy dx
k-space
La raccolta delle informazioni avviene, quindi, nel cosiddetto spazio K.
I metodi NMR Imaging sono organizzati in modo tale che si acquisisce
la “informazione” nello spazio K e l’immagine è ricostruita
semplicemente attraverso la trasformata di Fourier (2D) del segnale
spazio K.
FID(k x , k y )
ρ(x, y) e
x
ik y y
eik x x dy dx
y
Sia la codifica di frequenza che di fase possono essere
descritti attraverso un vettore k
k g Gt
FID(k x , k y ) ( x, y) exp[ i k r ]dxdy
x, y
k-space
FID(k x , k y )
x
Kx = g Gx t
ρ(x, y) e
ik y y
eik x x dy dx
y
kY
varia
costanti
kX
Ky = g t Gy
varia
costanti
Ogni punto rappresenta un FID
Campionamento spazio K
La trasformata di Fourier è definita su una linea dello spazio K.
La direzione di raccolta dei punti può essere definita tramite direzioni ortogonali che permettono
di esplorare tutto lo spazio K (coordinate cartesiane).
L’impulso di gradiente di campo Gy permette di spostarsi a quote diverse della direzione y dello
spazio K, mentre la successiva applicazione del gradiente Gx permette di raccogliere i punti K
lungo l’asse x ad una data quota y.
Ciò richiede che l’esperimento sia ripetuto per differenti valori di Ky.
kY
kX
Campionamento spazio K
/2
kY
rf
slice
read
kX
phase
Campionamento spazio K
linear phase encoding
/2
kY
rf
slice
read
phase
kX
multi slice imaging
Abbiamo visto che il tempo di acquisizione di un’immagine è uguale al prodotto del valore
TR (tempo di ripetizione) per il numero di passi relativi alla codifica di fase.
se TR =1 sec
e ci fossero 256 attivazioni del gradiente di codifica di fase
tempo totale di imaging richiesto per produrre un’immagine = 4,16 minuti
Se volessimo prendere 20 immagini di una regione di interesse, il tempo di imaging sarebbe
all’incirca di 1.5 ore (troppo lungo !!!!)
Osserviamo il diagramma temporale della sequenza di imaging con un TR di 1 sec:
la maggior parte del tempo della sequenza è inutilizzato
multi slice imaging
Durante questo tempo “inutilizzato” si potrebbe eccitare altri strati nell’oggetto esaminato.
l’unica limitazione è che l’eccitazione utilizzata per una fetta non deve influenzare un altra
fetta:
ciò può essere ottenuto applicando una certa intensità del gradiente di selezione e cambiando la
frequenza RF degli impulsi a 90°.
le tre bande di
frequenza degli
impulsi non si
sovrappongono
multi slice imaging
ci sono 3 impulsi RF, con picco
di frequenza n1, n2, e n3 ,
applicati nel periodo TR.
Di
conseguenza
gli
impulsi
interesseranno differenti fette
dell’oggetto esaminato.
Spin-echo Imaging
Spin-echo Imaging
kY
kX
phase
Vantaggio della sequenza spin-echo: segnale dipendente dal T2
Poiché alcuni tessuti e patologie hanno valori simili di T1 ma differenti valori di T2 è vantaggioso
avere una sequenza di imaging che produca immagini T2-dipendenti.
Spin-echo Imaging
Un impulso RF a 90o viene
applicato insieme con un
gradiente di selezione della
fetta.
Passa un periodo di tempo uguale a
TE/2 e viene applicato un impulso
a 180o in congiunzione con il
gradiente di selezione della fetta.
Spin-echo Imaging
Un gradiente di codifica di fase
viene applicato tra gli impulsi a 90°
e 180°
Esso è variato in 128 o 256 passi
Il gradiente di codifica in
frequenza viene applicato dopo
l'impulso a 180° durante il tempo
in cui viene raccolto l'echo.
Spin-echo Imaging
Un ulteriore gradiente viene applicato
tra gli impulsi a 90° e 180°.
Questo gradiente di defasamento agisce
lungo la stessa direzione del gradiente
di codifica in frequenza e sfasa gli spin
in modo che tornino in fase al centro
dell'echo.
Il gradiente di defasamento e' applicato per
posizionare l'inizio dell'acquisizione del
segnale all'estremità dello spazio-k
L'intera sequenza viene ripetuta ogni
TR secondi fino al completamento di
tutti i passi della codifica di fase.
Spin-echo Imaging
Immagini
acquisite con
SEQUENZA
SPIN ECHO
Per diversi valori di
TE (pesata in T2)
o
TR (pesata in T1)
Spin-echo Imaging
Immagini
acquisite con
SEQUENZA
SPIN ECHO
Per diversi valori di
TE
(pesate in T2)
TR molto grandi
Inversion recovery imaging
Inversion recovery imaging
Per osservare il segnale, dopo l’impulso di 90° si applica, con un prescelto ritardo τ,
un impulso di 180° per ottenere il segnale di eco: il segnale di eco è utilizzato al posto
del FID per la successiva trattazione matematica necessaria per produrre l’immagine.
Pertanto lo schema generale della sequenza IR è la seguente:
INVERSION RECOVERY : 180 –90 – 180
Una sequenza IR che utilizzi un 90-FID per la rivelazione del segnale e' del tutto simile,
con l'eccezione che un 90-FID prende il posto della componente spin echo della
sequenza.
Inversion recovery Imaging
INVERSION RECOVERY : 180 –90 – 180
CONTRASTO IN FUNZIONE DEL TEMPO DI
RECUPERO DELLA MAGNETIZZAZIONE
Viene applicato un impulso RF a 180o
selettivo di uno strato insieme con un
gradiente di selezione dello strato.
Inversion recovery Imaging
INVERSION RECOVERY : 180 –90 – 180
Trascorso un periodo di tempo uguale a
TI, viene applicata una sequenza spin-echo.
Inversion recovery Imaging
INVERSION RECOVERY : 180 –90 – 180
Il resto della sequenza e' equivalente ad
una sequenza spin-echo. Questa componente
spin-echo registra la magnetizzazione
presente al tempo TI dopo il primo impulso a
180°.
Tutti gli impulsi RF vengono applicati
insieme ai gradienti di selezione degli strati.
Inversion recovery Imaging
INVERSION RECOVERY : 180 –90 – 180
Tra gli impulsi di 90° e 180° viene
applicato un gradiente di codifica di fase. Il
gradiente di codifica di fase viene variato in
128 o 256 passi.
Il gradiente di codifica di fase non potrebbe
essere applicato dopo il primo impulso a 180o
perche' non c'e' la magnetizzazione trasversale
per codificare la fase a questo punto.
Il gradiente di codifica in frequenza viene
applicato dopo il secondo impulso a 180o
durante il periodo in cui viene raccolto
l'echo.
Il segnale registrato e' l'echo.
Il FID dopo l'impulso a 90o non viene utilizzato. Il gradiente di defasamento e' applicato tra gli impulsi
a 90o e 180o per posizionare l'inizio dell'acquisizione del segnale all'estremità dello spazio-k, come e'
stato già descritto nella sezione sull'imaging con sequenze spin-echo. L'intera sequenza viene ripetuta
ogni TR secondi.
Inversion recovery Imaging
Immagini
acquisite con
SEQUENZA
Inversion
Recovery
Per diversi valori di
TR e TI
(pesate in T1)
Imaging Gradient Echo
Le sequenze di imaging viste fin ora hanno un grande svantaggio: per ottenere il massimo
segnale richiedono tutte che la magnetizzazione trasversale riacquisti la sua posizione di
equilibrio lungo l’asse Z prima che venga ripetuta la sequenza.
Quando il T1 è lungo, questo può prolungare in modo significativo la sequenza di
imaging. Se la magnetizzazione non riacquista in modo completo l’equilibrio il segnale è
minore di quello che si avrebbe nel caso del completo recupero.
Infatti, come si è visto nelle sequenze utilizzate per ottenere le immagini T1-pesate, al
diminuire del TR anche il segnale decresce.
Imaging Gradient Echo
Se la magnetizzazione viene ruotata di un angolo q minore di 90° la sua componente
Mz riacquisterà l’equilibrio molto più rapidamente, ma ci sarà un minor segnale dal
momento che il segnale è proporzionale al senq.
Così perdiamo segnale a vantaggio del tempo di imaging.
In alcuni casi, possono essere raccolte e mediate insieme più immagini per recuperare
il segnale perduto. La sequenza di imaging gradient echo è l’applicazione di questi
principi.
Imaging Gradient Echo
Abbiamo ampiamente visto che in presenza di un gradiente di campo magnetico, le
componenti di magnetizzazione defasano.
Di conseguenza i FID decadono più velocemente che in assenza di un gradiente. Ogni
defasamento deve essere rifocalizzato in un eco.
La rifocalizzazione può essere ottenuta sia da un impulso rf (Hahn echoes) sia da
manipolazioni di gradiente (gradient echoes).
Nell’imaging gradient echo, un segnale di eco si ottiene senza fare uso dell'impulso
di 180°, ma attraverso la manipolazione di gradiente.
Cerchiamo ora di comprendere come ciò sia possibile e i vantaggi e gli svantaggi che
si hanno nell'uso di tale eco.
Imaging Gradient Echo
Inviamo al sistema di spin un impulso di 90° e durante il segnale di FID sia presente
un gradiente di campo magnetico lineare, applicato per un tempo Δt.
A scopo puramente didattico, in questa prima fase della trattazione, trascuriamo
fenomeni di sfasamento dovuti alla interazione tra gli spin (campi locali responsabili
del T2) ed alle disomogeneità del campo magnetico statico Bo, indipendenti dal
tempo.
A causa della presenza del gradiente, ha origine uno sfasamento degli spin
Imaging Gradient Echo
Fissiamo la nostra attenzione solo su due isocromatici (stessa frequenza), a e b,
simmetrici rispetto all'isocentro (punto nel quale il campo vale sempre Bo) di
coordinate + z e - z rispettivamente
Imaging Gradient Echo
Nel tempo Δt (durata dell’impulso di gradiente negativo) i due isocromatici
effettuano una rotazione data da:
a g (G)( z)t
e
b g (G)( z)t
Imaging Gradient Echo
se a questo istante invertiamo il segno del gradiente, cioè il gradiente passa da -G a +G, applicandolo
per un pari intervallo di tempo Δt, i due isocromatici effettueranno ora una ulteriore rotazione
a gG( z)t e b gG( z )t
pertanto dopo un tempo pari a 2Δt l'angolo
spazzato sarà per i due isocromatici
cioè dopo un tempo 2Δt
i due isocromatici sono
di nuovo in fase, e si
avrà il massimo segnale
chiamato
"eco di gradiente "
Imaging Gradient Echo
Nella sequenza di imaging gradient echo viene applicato:
un impulso RF selettivo di strato all’oggetto da esaminare che produce tipicamente un angolo di
rotazione fra 10° e 90° (cioè non è più necessario usare un 90°);
un gradiente di selezione della fetta;
un gradiente di codifica di fase (variato in 128 o 256 passi);
un gradiente defasante di codifica in frequenza viene applicato simultaneamente al gradiente di
codifica di fase. Questo gradiente è di segno negativo.
Un echo è prodotto quando si attiva il gradiente di codifica di frequenza perché questo gradiente
recupera la perdita di fase avvenuta a causa del gradiente defasante.
Un periodo chiamato tempo di echo (TE) è definito come il tempo intercorrente fra l’inizio dell’impulso
RF ed il massimo nel segnale.
La sequenza viene ripetuta ogni TR secondi. Il periodo TR è dell’ordine delle decine di millisecondi.
Imaging Gradient Echo
In questo modo non facendo uso dell'impulso di 180° è possibile avere TE molto più corti con
un aumento del rapporto segnale rumore.
Inoltre necessitando meno potenza RF, il sistema di amplificatori RF può lavorare con TR
molto corti, permettendo l'uso delle sequenze veloci.
q
Il flip-angle può essere ottimizzato
per il massimo rapporto segalerumore, fissato il TR.
Tipicamente i flip-angles sono
dell’ordine di 15°. L’intensità del
FID
dopo
questo
impulso
corrisponde al 25%
(sen15°)
dell’intensità dopo l’impulso a 90°.
Tuttavia, più del 96% (cos 15°)
della magnetizzazione longitudinale
(Mz) è preservata per permettere i
passi veloci di ripetizione.
Imaging Gradient Echo
Immagini
acquisite con
ECO di
GRADIENTE
(GE)
per diversi
valori di
TR e q
Imaging Gradient Echo
GRADIENT ECHO: CONSIDERAZIONI
Nella trattazione precedente abbiamo trascurato gli sfasamenti dovuti alla
interazione tra gli spin ed alle disomogeneità del campo magnetico statico Bo.
Questi sfasamenti sono sempre presenti e contribuiscono al decadimento del
segnale.
In particolare è importante rilevare che il procedimento che porta alla formazione
del segnale di eco di gradiente, non annulla lo sfasamento degli spin generato
dalle disomogeneità del campo Bo, come invece accadeva nel caso della sequenza
SE con impulso di 180°.
Pertanto i segnali saranno molto più dipendenti da tali disomogeneità, comprese
quelle locali che esistono nelle discontinuità tessutali dovute alle variazioni di
suscettività magnetica.
CONTRASTO
Affinché siano visibili una patologia o un qualsiasi tessuto di interesse in
un’immagine di risonanza magnetica è necessario che ci sia contrasto ovvero
una differenza nell’intensità di segnale tra esso ed i tessuti adiacenti.
L’intensità del segnale, S, è determinata dall’equazione del segnale per la
specifica sequenza utilizzata. Alcune delle variabili intrinseche sono:
Il tempo di rilassamento spin-reticolo, T1
Il tempo di rilassamento spin-spin, T2
La densità degli spin,
Il T2*
Le variabili strumentali sono:
Il tempo di ripetizione, TR
Il tempo di echo, TE
Il tempo di inversione, TI
L’angolo di rotazione, q
Il T2*
T2* compare in entrambe le liste perche'
contiene una componente dipendente
dall'omogeneita' del campo magnetico ed
una dipendente dai movimenti molecolari.
CONTRASTO
Le equazioni del segnale per le sequenze di impulsi presentate fin ora sono:
In ognuna di queste equazioni, S rappresenta l'ampiezza del segnale nello spettro del dominio della frequenza. La quantita'
k e' una costante di proporzionalita' che dipende dalla sensibilita' del circuito di rivelazione del segnale. I valori di T1, T2 e
sono specifici per un tessuto o una patologia.
Spin-Echo
Inversion-Recovery (180-90)
S k (1 e TR / T 1 ) e TE / T 2
S k (1 2eTI / T 1 eTR / T 1 )
CONTRASTO
Inversion-Recovery (180-90-180)
S k (1 2e TI / T1 e TR / T1 ) e TE / T 2
q
Gradient Echo
S k
(1 e TR / T 1 )
(1 cosq e TR / T 1 )
senq e TE / T 2*
CONTRASTO
La seguente tabella elenca il range dei valori di T1, T2, e a 1.5 Tesla per tessuti riconoscibili in
un’immagine di risonanza magnetica della testa umana.
Tissue
T1 (s)
T2 (ms)
CSF
0.8 - 20
110 - 2000
70-230
Materia bianca
0.76 - 1.08
61-100
70-90
Materia grigia
1.09 - 2.15
61 - 109
85 - 125
Meningi
0.5 - 2.2
50 - 165
5 - 44
Muscolo
0.95 - 1.82
20 - 67
45 - 90
Grasso
0.2 - 0.75
53 - 94
50 - 100
Il tessuto cerebrale è composto di materia grigia e di materia bianca: la prima
comprende i centri funzionali del sistema nervoso centrale, mentre nelle regioni della
materia bianca sono presenti fasci di fibre che connettono tali centri.
CSF = cerebrospinal fluid
Reference:
L.M. Fletcher, J.B. Barsotti, J.P. Hornak "A Multispectral Analysis of Brain Tissues“ Magn. Reson. Med. 29:623 (1993).
CONTRASTO
Il contrasto, C, tra due tessuti A e B sara' uguale alla differenza fra il segnale per il tessuto A, SA, e
quello per il tessuto B, SB.
C = S A - SB
SA e SB sono determinati dalle equazioni del segnale date sopra.
Per ogni coppia di tessuti ci sara' un insieme di parametri che producono un contrasto massimo.
Ad esempio, in una sequenza spin-echo il contrasto fra due tessuti in funzione del TR e' rappresentato
graficamente nella curva riportata.
La curva del contrasto per i tessuti A e B in funzione del TE è rappresentata nella curva riportata.
CONTRASTO
Si adotta una nomenclatura per esprimere il meccanismo di contrasto predominante in un'immagine.
Le immagini il cui contrasto e' causato prevalentemente dalle differenze dei T1 dei tessuti, sono
chiamate immagini T1-pesate.
Similmente per il T2 e per , le immagini sono chiamate T2-pesate e DP-pesate (pesate in densita'
protonica).
La seguente tabella contiene l'insieme delle condizioni necessarie per ottenere immagini pesate.
Pesatura
TR
TE
T1
< = T1
< < T2
T2
> > T1
> = T2
> > T1
< < T2
CONTRASTO
Immagini spin-echo
TR (ms)
Vediamo come la scelta dei
parametri strumentali TR,
250
TE, TI e q ha effetto sul
contrasto tra i vari tessuti
500
del cervello.
750
Le
immagini
spin-echo
sono reali immagini di
risonanza magnetica del
1000
cervello umano.
2000
20
TE (ms)
40
60
80
CONTRASTO
TI (ms)
50
Immagini
inversion-recovery
100
(180-90)
250
500
750
TR (ms)
1000
2000
CONTRASTO
q (°)
15
Immagini
gradien echo
(TE = 5ms)
30
45
60
90
25
TR (ms)
50
100
200