le isometrie

G
E
O
M
E
T
R
I
A
Esplorare la Geometria
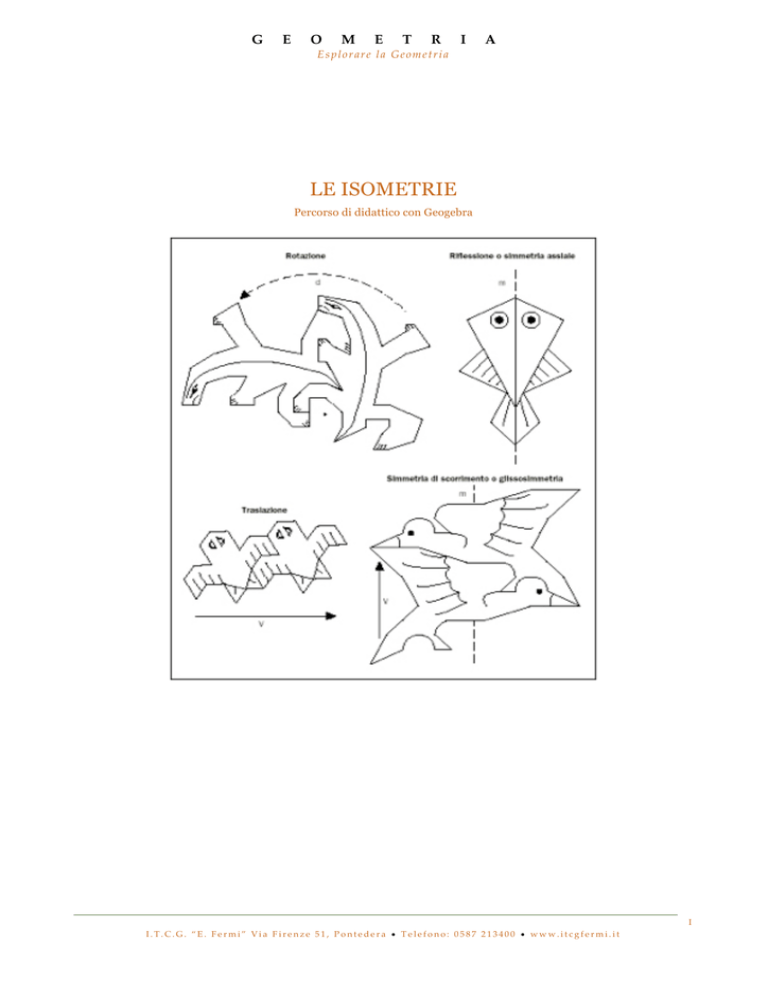
LE ISOMETRIE
Percorso di didattico con Geogebra
I
I.T.C.G. “E. Fermi” Via Firenze 51, Pontedera • Telefono: 0587 213400 • www.itcgfermi.it
Introduzione
Lo scopo di questo volume è quello di fornire materiale agli insegnanti di matematica che vogliono sperimentare la didattica laboratoriale guidando gli studenti attraverso un percorso nel quale “si impara facendo” o meglio “costruendo”; siamo convinte che un modo interessante per appassionare gli studenti sia quello di lasciarli liberi di osservare ed esplorare
la realtà per poi giungere a conclusioni che si possono trasformare a loro volta in definizioni, proprietà, teoremi.
Questa prima esperienza è rivolta in particolare agli studenti del biennio e riguarda la isometrie utilizzando il software
free Geogebra. Insieme alle schede sono fornite le costruzioni con la possibilità di riprodurle in classe con un solo clic!
1
Scheda 01
SIMMETRIA ASSIALE
Obiettivi:
• Saper eseguire il ribaltamento di un punto rispetto ad un asse;
• Saper riconoscere le caratteristiche di due punti simmetrici rispetto ad un asse.
Esecuzione:
a) Usando il comando “Punto”, traccia un punto sul piano a tua scelta e assegnagli il nome P (tasto
destro e poi “Rinomina”).
b) Usando il comando “Retta per due punti”, traccia una retta per due punti A e B diversi da P ed
assegnale il nome r.
c) Dalla barra degli Strumenti clicca sulla casella “Simmetrico rispetto ad una retta” e trova il
simmetrico del punto.
d) Assegna il nome P’ al punto ottenuto.
Il punto P’ è il simmetrico del punto P rispetto alla retta r
e)
f)
g)
h)
Unisci con un segmento i punti P e P’.
Seleziona il comando “Distanza o lunghezza”.
Verifica la distanza del punto P dalla retta r (clic sul punto P, poi clic sulla retta r) .
Verifica la distanza del punto P’ dalla retta r. Cosa noti?
_________________________________________________________________
i) Clicca su “Intersezione fra due oggetti” e trova il punto di incontro tra la retta r ed il segmento
PP’.
j) Clicca su “Angolo” e misura l’angolo tra il segmento e la retta (Attenzione: la misura dell’angolo
viene fatta in senso orario).
k) In che posizione si trova il segmento PP’ rispetto alla retta r?
_________________________________________________________________
Il punto P’ è simmetrico al punto P rispetto alla retta r se il segmento che unisce P con P’ è
__________________ alla retta r e la distanza tra il punto P e la ______________ è uguale
alla distanza tra _____________________________
Si dice simmetria assiale la trasformazione che, data una retta r, associa ad ogni punto P del piano il suo simmetrico rispetto ad r.
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
2
Scheda 01 (Bis)
SIMMETRIA ASSIALE
Obiettivi:
• Saper costruire la perpendicolare ad una retta r passante per un punto C esterno alla retta r.
Esecuzione:
a) Come hai costruito la perpendicolare alla retta r passante per il punto P?
__________________________________________________________________
b) Prova ad eseguire la costruzione della perpendicolare proposta da Euclide.
a.
b.
c.
d.
e.
f.
g.
Usando il tasto “Punto” traccia un punto sul piano a tua scelta e assegnagli nome P.
Usando il comando “Retta per due punti” traccia una retta e dagli nome r.
Considera un punto a piacere C dall’altra parte della retta r rispetto a P.
Traccia la circonferenza di centro P e raggio PC utilizzando il comando “Circonferenza di
dato centro”.
Utilizza il comando “Intersezione di due oggetti” e trova i punti D ed E di intersezione tra
la circonferenza e la retta r.
Costruisci i segmenti PD e PE. Come sono? _______________________________
Perchè? _______________________________________________________
Adesso devi costruire la perpendicolare, puoi utilizzare due modi:
• Costruisci il punto medio del segmento DE inserendo nella barra in basso la seguente
scrittura D+1/2(E-D). Chiama F il punto medio costruito. Unisci il punto P col punto
F utilizzando il comando “Retta per due punti” e chiamala s. Verifica che la retta r e la
retta s sono perpendicolari.
Per eseguire anche la seguente costruzione vai sulla retta s e col tasto destro scegli
“Mostra oggetto”, in questo modo la costruzione precedente non viene persa ma non
viene visualizzata.
• Costruisci due circonferenze: la prima di centro D e raggio DE, la seconda di centro E
e raggio ED. Chiama G il punto in cui le due circonferenze si incontrano dalla parte
opposta di P rispetto alla retta r. Utilizzando il comando “Retta per due punti” traccia
la retta s passante per i punti P e G. Verifica che la retta r e la retta s siano
perpendicolari.
Due rette r e s si dicono perpendicolari se, incontrandosi, formano tra loro quattro angoli retti
c) Una volta trovata la retta perpendicolare, trova il punto P’ simmetrico al punto P. Quale
procedura hai utilizzato?
____________________________________________________________________
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
3
Scheda 02
SIMMETRIA ASSIALE
Obiettivi:
• Saper eseguire il ribaltamento di un segmento rispetto ad un asse.
Esecuzione:
a) Usando la casella degli Strumenti “Segmento” costruisci un segmento di estermi A e B.
b) Usando il comando “Retta per due punti” traccia una retta ed assegnale il nome r.
c) Dalla barra degli Strumenti clicca sulla casella “Simmetrico rispetto ad una retta”: seleziona il
segmento AB e poi la retta r. Assegna agli estremi del nuovo segmento i nomi A’ e B’.
d) Verifica la lunghezza dei segmenti AB e A’B’ attraverso il comando “Distanza o lunghezza”.
Come sono i segmenti?
_________________________________________________________________
e) Costruisci i segmenti AA’ e BB’.
f) Individua il punto di intersezione tra il segmento AA’ e la retta r e assegna il nome O.
g) Individua il punto di intersezione tra il segmento BB’ e la retta r e assegna il nome K.
h) Misura la distanza del punto A dal punto O e la distanza dal punto O al punto A’. Che cosa noti?
_________________________________________________________________
i) Ripeti la procedura per i segmenti BK e KB’.
j) Che cosa rappresenta per i segmenti AA’ e BB’ la retta r (quali caratteristiche osservi?)?
_________________________________________________________________
k) In che posizione si trovano i segmenti AA’ e BB’ ’ rispetto alla retta r ?
_________________________________________________________________
La retta perpendicolare ad un segmento nel suo punto medio si dice asse del segmento
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
4
Scheda 03
SIMMETRIA ASSIALE
Obiettivi:
• Saper eseguire il ribaltamento di una figura rispetto ad un asse;
• Saper disegnare, identificare punti e figure simmetriche rispetto a una retta;
• Saper riconoscere le caratteristiche di due figure simmetriche rispetto ad un asse.
Esecuzione:
a) Usando la casella degli Strumenti “poligono” costruisci una figura ABC.
b) Usando il comando “Retta per due punti” traccia una retta r alla destra del triangolo ABC.
c) Dalla barra degli Strumenti clicca sulla casella “Simmetrico rispetto ad una retta”: seleziona il
triangolo ABC e poi la retta r. Assegna alla nuova figura i punti corrispondenti A’B’C’.
d) Come sono disposte le lettere del triangolo alla tua sinistra: in senso orario o antiorario?
_________________ E quelle del triangolo alla tua destra? ______________________
e) Le due figure si possono dire congruenti? ____________________________________
f) Clicca su “Relazione fra due oggetti” e poi sui due triangoli. Che cosa osservi?
_________________________________________________________________
Poiché i versi di percorrenza dei loro contorni sono opposti si tratta di congruenza inversa
g) Immagina di voler sovrapporre le due figure in modo che i punti corrispondenti coincidano. La
seconda figura si muove per andare a sovrapporsi alla prima, il movimento avviene sul piano
(lo schermo del PC) o nello spazio (uscendo dallo schermo del PC)?
_________________________________________________________________
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
Figura simmetrica rispetto ad un asse
5
Scheda 03 (Bis)
SIMMETRIA ASSIALE
Obiettivi:
• Saper riconoscere figure simmetriche rispetto ad un asse.
Esecuzione:
a) Costruisci un triangolo ABC utilizzando il comando “Poligono regolare”: digita due punti e
quando compare la finestra di dialogo inserisci il numero 3.
b) Attraverso il comando “Distanza o lunghezza” mostra le lunghezze dei lati AB, BC, CA. Che cosa
osservi? ___________________________________________________________
Un triangolo equilatero è un poligono regolare con tre lati
c) Attraverso il comando “Retta perpendicolare” costruisci la perpendicolare r al lato BC passante
per il punto A: chiama D l’intersezione della retta r con il lato BC.
d) Con il comando “Distanza o lunghezza” misura i segmenti BD e DC: riesci a riconoscere una
simmetria?
_________________________________________________________________
e) Che cosa puoi osservare sul punto A?
_________________________________________________________________
f) Ripeti la procedura costruendo la perpendicolare al lato AB passante per C e la perpendicolare
al lato AC passante per B. Quanti assi di simmetria puoi ottenere contemporaneamente in un
triangolo equilatero?
_________________________________________________________________
g) Costruisci ora un quadrato utilizza il comando “Poligono regolare”: digita due punti e quando
compare la finestra di dialogo inserisci il numero 4. Quanti assi di simmetria puoi trovare?
_________________________________________________________________
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
6
Costruzioni di Euclide
Nella schede precedente ti veniva chiesto di costruire un triangolo equilatero ed un quadrato per
poter riconoscere le simmetrie assiali presenti nelle due figure.
Ma come hai costruito il triangolo equilatero? E il quadrato?
Di seguito sono riportate le costruzioni proposte da Euclide nel suo libro “Gli Elementi”; prova a
fare la costruzione sul tuo quaderno.
Libro I, Proposizione 1: Triangolo equilatero
Libro I, Proposizione 46: Quadrato
Libro I, Proposizione 11: Perpendicolare ad
una retta passante per un punto appartenente alla retta stessa
7
Scheda 03 (Tris)
SIMMETRIA CENTRALE
Obiettivi:
• Saper costruire figure simmetriche rispetto ad un punto.
Esecuzione:
a) Usando il comando “Punto” traccia un punto sul piano a tua scelta e assegnagli il nome P (tasto
destro e poi “Rinomina”).
b) Ripeti la procedura e considera il punto O.
c) Utilizzando il comando “Simmetrico rispetto ad un punto” costruisci il simmetrico del punto P
rispetto al punto O e chiamalo P’.
d) Quali osservazioni puoi fare nei confronti dei segmenti Po e OP’?
_________________________________________________________________
Si dice simmetria centrale di centro O la trasformazione
che ad ogni punto P del piano associa il suo simmetrico P’ rispetto a O
e) Usando il comando “Poligono” traccia un generico quadrilatero ABCD.
f) Usando il comando “Punto” costruisci un punto alla destra del quadrilatero e chiamalo O’.
g) Attraverso il comando “Simmetrico rispetto ad un punto” costruisci il simmetrico del
quadrilatero ABCD rispetto al punto O’.
h) Come sono disposte le lettere del poligono alla tua sinistra: in senso orario o antiorario?
_________________ E quelle del poligono alla tua destra? ______________________
i) Le due figure si possono dire congruenti? ____________________________________
j) Clicca su “Relazione fra due oggetti” e poi sui due poligoni. Che cosa osservi?
_________________________________________________________________
L’ordinamento dei punti è invariante
k) Costruisci i segmenti AO’, BO’, CO’, DO’ che hanno determinato la simmetria e verifica le
lunghezze.
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
2
Scheda 04
TRASLAZIONE
Obiettivi:
• Capire il significato di Traslazione
Esecuzione:
a)
b)
c)
d)
Usando la casella degli Strumenti “Triangolo” costruisci una figura ABC.
Clicca su “Muovi”.
Seleziona la figura e trascinala sul piano.
Puoi ripetere più volte.
Hai spostato o meglio hai traslato la figura sul piano.
Il movimento che hai effettuato si dice traslazione
Dopo aver disegnato una figura sulla scheda o sul quaderno ricalca la figura su un foglio trasparente, segna i vertici corrispondenti A’B’C’, fai scivolare sul piano il foglio trasparente. Verifica varie
traslazioni.
Traslazione di una figura con l’utilizzo di carta trasparente
3
Scheda 05
TRASLAZIONE DI UN PUNTO E DI UN SEGMENTO
Obiettivi:
• Eseguire la traslazione di un punto secondo un vettore noto
• Eseguire la traslazione di un segmento secondo un vettore noto
Esecuzione:
a) Usando il comando “Punto” traccia un punto sul piano: assegna a questo punto il nome A.
b) Usando la casella degli strumenti “Segmento” costruisci un segmento BC e chiamalo b.
c) Traccia sul piano un vettore DE, usando il tasto “Vettore tra due punti” e chiamalo v.
Il vettore rappresenta la direzione, il verso e l’intensità del movimento di traslazione.
La direzione è la retta a cui appartiene, il suo verso è il senso di percorrenza, la sua intensità è
la lunghezza del segmento
d) Usando il comando “Trasla di un vettore” seleziona prima il punto A e poi il vettore. Cosa
succede? ___________________________________________________________
e) Ora trasla anche il segmento BC. Cosa succede? ________________________________
f) Seleziona il comando “Distanza o lunghezza” e verifica la lunghezza del vettore ___________
g) Unisci il punto A con il punto A’ utilizzando il tasto “Segmento”. Misura la lunghezza del
segmento AA’ __________
h) Unisci il punto B con B’ e poi il punto C con C’. Misura la lunghezza del segmento BB’
________________ e del segmento CC’ _________
i) Quali osservazioni puoi fare considerando il vettore e i segmenti AA’, BB’, CC’?
_________________________________________________________________
Si dice traslazione di un vettore v la trasformazione che ad ogni punto P del piano associa il suo
traslato P’ mediante il vettore v
j) Utilizzando i comandi di Geogebra prova a costruire la traslazione di un punto P e di un
segmento AB senza utilizzare la procedura “Trasla di un vettore”. Quali comandi hai eseguito?
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
4
Scheda 06
TRASLAZIONE DI UN TRIANGOLO
Obiettivi:
• Eseguire la traslazione di un triangolo secondo un vettore noto
• Saper individuare le proprietà che caratterizzano una traslazione
Esecuzione:
a) Usando la casella degli Strumenti “Triangolo” costruisci una figura ABC
b) Traccia sul piano un vettore, e chiamalo v.
c) Trasla il triangolo secondo il vettore v. Cosa succede?
________________________________________________________________________
La figura ha fatto un movimento la cui direzione, verso e lunghezza sono determinati dal vettore.
Le due figure sono congruenti? ______________________ (Usa “Relazione fra due oggetti”).
d) Come sono disposte le lettere del triangolo alla tua sinistra? In senso orario o antiorario?
__________________ E quelle del triangolo alla tua destra? _____________________
Poiché i versi di percorrenza dei loro contorni sono uguali si tratta di congruenza diretta
e) Seleziona il comando “Distanza o lunghezza”
f) Clicca sul vettore e segna la misura della sua lunghezza ___________________
g) Ora clicca sul punto A e poi sul punto A’:
1. Quanto misura la distanza AA’? ______________________________________
2. Quanto misura la distanza BB’? ______________________________________
3. Quanto misura la distanza CC’? ______________________________________
4. Che cosa puoi notare? _____________________________________________
h) Disegna i segmenti che uniscono i punti A e A’, B con B’ e C con C’. Immaginiamo che questi
segmenti siano le “tracce” lasciate dai punti che si muovono. Che cosa noti?
_________________________________________________________________
i) Completa allora la frase che indica la proprietà che caratterizza la traslazione:
Una traslazione trasforma i punti A B C del piano nei punti A’ B’ C’ ottenendo segmenti AA’ BB’
CC’ tutti _______________________ e ______________________________tra loro.
j) Prova a ripetere la procedura per altri poligoni e secondo altri vettori di traslazione.
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
5
Scheda 06 (Bis)
ROTAZIONE
Obiettivo:
• Capire il significato di Rotazione
Esecuzione:
a) Disegna due punti: P e O.
b) Utilizzando il comando “Ruota intorna a un punto di un angolo” clicca prima sul punto P, poi
sul punto O e poi inserisci un valore per l’angolo.
c) Chiama P’ il punto trovato.
d) Costruisci i segmenti PO e OP’: che cosa osservi? _______________________________
e) Misura l’angolo POP’ e l’angolo P’OP: che cosa osservi? ___________________________
Ad ogni angolo è associato un verso orario oppure antiorario
f) Qual è l’angolo che corrisponde alla rotazione che hai effettuato? ____________________
Si dice rotazione di centro O e ampiezza la trasformazione che ad ogni punto P del piano
associa il punto P’ ottenuto ruotando il punto P intorno al punto O di un angolo orientato .
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
6
Scheda 07
ROTAZIONE
Obiettivo:
• Imparare a ruotare un segmento
• Imparare a ruotare un triangolo
Esecuzione:
a) Disegna un segmento AB.
b) Segna sul piano un punto O.
c) Clicca su “Ruota intorno ad un punto di un angolo”: clicca sul segmento, poi sul punto e scegli
un angolo a piacere.
d) Costruisci i segmenti AO, OA’: cosa noti? _____________________________________
e) Costruisci i segmenti BO, OB’: cosa noti? _____________________________________
f) Misura gli angoli AOA’ e BOB’: cosa osservi? __________________________________
g) Disegna un triangolo ABC.
h) Segna sul piano un punto O.
i) Clicca su “Ruota intorno ad un punto di un angolo”: clicca sul segmento, poi sul punto e scegli
un angolo a piacere.
j) Costruisci i segmenti AO, OA’: cosa noti? _____________________________________
k) Costruisci i segmenti BO, OB’: cosa noti? _____________________________________
l) Costruisci i segmenti CO, OC’: cosa noti? _____________________________________
m) Misura gli angoli AOA’, BOB’ e COC’: cosa osservi? ______________________________
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
Dopo aver disegnato una figura sulla scheda o sul quaderno, ricalca la figura su un foglio trasparente, segna i vertici corrispondenti A’B’C’ e fai ruotare il foglio trasparente attorno ad un puntina (che
fissa il foglio e la carta trasparente).
7
Scheda 08
RIEPILOGO
Obiettivi:
•
•
•
•
•
•
Riconoscere varianti e invarianti nelle figure simmetriche;
Capire che la simmetria è un’isometria;
Riconoscere varianti e invarianti nelle figure traslate;
Capire che la traslazione è un’isometria;
Riconoscere varianti e invarianti nelle figure ruotate;
Capire che la rotazione è un’isometria;
Si dicono invarianti di una trasformazione geometrica
le caratteristiche che rimangono inalterate nella trasformazione.
a) Nella scheda della simmetria assiale, il triangolo ABC ed il suo simmetrico A’B’C’ erano
congruenti? ______________________________________________________
b) Prova a ricostruire la trasformazione e verifica la congruenza delle due figure. Che cosa
osservi? _________________________________________________________
c) Ripeti lo stesso esercizio per il triangolo ABC che hai ottenuto nella traslazione, nella
rotazione e nella simmetria centrale. Che cosa osservi?
Traslazione: ______________________________________________________
Rotazione: _______________________________________________________
Simmetria centrale: ________________________________________________
d) Le trasformazioni viste fino a questo punto sono particolari trasformazioni che modificano
soltanto la posizione delle figure nel piano, le figure trasformate sono tra loro tutte
congruenti.
e) Prova ad elencare quali sono le invarianti di queste trasformazionie:
Cosa puoi dire della misura dei segmenti che si corrispondono: ___________________
Cosa puoi dire dell’ampiezza degli angoli che si corrispondono: ___________________
Cosa puoi dire delle rette parallele: ______________________________________
Si dice isometria la trasformazione geometrica che
ad ogni coppia di punti A e B di un piano
associa i punti A’ e B’ dello stesso piano in modo che
il segmento AB sia congruente al segmento A’B’.
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
8
Scheda 09
LA RETTA: SIMMETRIA ASSIALE
Obiettivi:
• Saper eseguire il ribaltamento di una retta rispetto ad un asse.
Esecuzione:
a) Usando il comando “Retta per due punti”, traccia una retta ed assegnale il nome r. Questa sarà
l’asse di simmetria.
b) Costruisci una retta che sia parallela ad r e assegnale il nome a.
c) Dalla barra degli Strumenti clicca sulla casella “Simmetrico rispetto ad una retta”.
d) Seleziona la retta a e poi la retta r.
e) Assegna alla nuova retta il nome a’.
f) Come sono tra loro le retta a e a’? Come puoi verificarlo?
_________________________________________________________________
g) Costruisci una retta che sia perpendicolare ad r e assegnale il nome b.
h) Dalla barra degli Strumenti clicca sulla casella “Simmetrico rispetto ad una retta”.
i) Seleziona la retta b e poi la retta r.
j) Quale è la simmetrica della retta b?
_________________________________________________________________
k) Costruisci una retta che sia incidente, ma non perpendicolare ad r e assegnale il nome c.
l) Dalla barra degli Strumenti clicca sulla casella “Simmetrico rispetto ad una retta”.
m) Seleziona la retta c e poi la retta r. Chiama la retta ottenuta c’.
n) Come è la retta c’ rispetto alla r? Le tre rette hanno qualche punto in comune?
_________________________________________________________________
o) Secondo te cosa rappresenta la retta r per l’angolo formato dalle rette c e c’?
_________________________________________________________________
p) Verifica le tue conclusioni misurando gli angoli.
q) Completa allora la frase seguente:
Una simmetria assiale trasforma una retta del piano in un’altra retta.
A seconda della posizione della retta di partenza rispetto all’asse di simmetria possiamo concludere
che:
1. la simmetrica di una retta parallela all’asse di simmetria è ______________ alla retta
di partenza;
2. la simmetrica di una retta perpendicolare all’asse di simmetria è _________;
3. la simmetrica di una retta incidente all’asse di simmetria è ancora ________ alla retta
di partenza e l’asse di simmetria rappresenta ________________.
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
9
Scheda 10
LA RETTA: ROTAZIONE E SIMMETRIA CENTRALE
Obiettivi:
• Saper eseguire la rotazione di una retta rispetto ad un punto.
Esecuzione:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
Traccia un punto sul piano e assegnagli il nome C. Questo sarà il centro della rotazione.
Costruisci una retta che non passi per C e assegnale il nome a.
Clicca su “Ruota intorno ad un punto di un angolo”.
Clicca sulla retta, poi sul punto e scegli un angolo a piacere.
Assegna alla nuova retta il nome a’.
Come sono tra loro le rette a e a’? __________________________________________
Costruisci una retta che passi per C e assegnale il nome b.
Clicca su “Ruota intorno ad un punto di un angolo”.
Clicca sulla retta, poi sul punto e scegli un angolo a piacere.
Come sono tra loro le rette b e b’? __________________________________________
Ripeti le rotazioni precedenti fissando però un angolo di 180°.
Come sono tra loro le rette a e a’, b e b’? Come puoi verificarlo? ______________________
Una simmetria centrale trasforma una retta del piano in un’altra retta.
A seconda della posizione della retta di partenza rispetto al centro di simmetria possiamo
concludere che:
1. la simmetrica di una retta non passante per il centro di simmetria è _____________;
2. la simmetrica di una retta passante per il centro di simmetria è ________________.
Una rotazione trasforma una retta del piano in un’altra retta.
A seconda della posizione della retta di partenza rispetto al centro di rotazione possiamo
concludere che:
1. la simmetrica di una retta non passante per il centro di rotazione è ______________;
2. la simmetrica di una retta passante per il centro di rotazione è _________________;
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
10
Scheda 11
LA RETTA: TRASLAZIONE
Obiettivi:
• • Saper eseguire la traslazione di una retta rispetto ad un vettore
Esecuzione:
a) Traccia sul piano un vettore, e chiamalo v. Questo sarà il vettore della traslazione.
b) Costruisci una retta che non parallela a v e assegnale il nome a.
c) Usando il comando “Trasla di un vettore” seleziona prima la retta e poi il vettore. Cosa succede?
Come puoi verificare la posizione delle rette a e a’? ______________________________
d) Costruisci una retta che parallela a v e assegnale il nome b.
e) Usando il comando “Trasla di un vettore” seleziona prima la retta b e poi il vettore. Cosa
succede? ___________________________________________________________
Una traslazione trasforma una retta del piano in un’altra retta.
A seconda della posizione della retta di partenza rispetto al vettore possiamo concludere che:
1. la traslata di una retta non parallela al vettore è ___________________________;
2. la traslata di una retta parallela al vettore è ______________________________.
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
11
Scheda 12
APPROFONDIMENTI (per casa)
Obiettivi:
• Approfondire concetto di asse di un segmento e di bisettrice di un angolo;
• Approfondire concetto di perpendicolarità.
Esecuzione:
a) Rileggi attentamente le schede iniziali.
b) Cerca la definizione di rette perpendicolari.
_________________________________________________________________
c) Cerca di trovare altre definizioni di rette perpendicolari usando le isometrie studiate.
_________________________________________________________________
d) Cerca la definizione di asse di un segmento.
_________________________________________________________________
e) Cerca di trovare altre definizioni di asse di un segmento usando le isometrie studiate.
_________________________________________________________________
f) Cerca la definizione di bisettrice di un angolo.
_________________________________________________________________
g) Cerca di trovare altre definizioni di bisettrice usando le isometrie studiate.
_________________________________________________________________
12
Scheda 13
APPROFONDIMENTI: INDIVIDUARE LE ISOMETRIE
Obiettivi:
• Saper individuare assi e centri di simmetria o rotazione;
• Saper individuare vettori che generano la traslazione.
Esecuzione:
a) Usando l’inserimento manuale, disegna i punti A(1;2), B(-1;3), C(-2;6), D(0;5), A’(1;2), B’(3;1),
C’(6;2), D’(4;3).
b) Disegna i quadrilateri ABCD e A’B’C’D’.
c) Usando il comando “Relazione fra due oggetti” verifica che i quadrilateri sono congruenti.
d) Cerca di trovare l’asse di simmetria in modo da trasformare il quadrilatero ABCD nel
quadrilatero A’B’C’D’. Ricorda che l’asse di simmetria deve essere ________ del segmento che
unisce due punti corrispondenti.
e) Verifica che la retta che hai trovato è veramente l’asse di simmetria. Come lo verifichi? ______
_________________________________________________________________
f) Ripeti il procedimento con i quadrilateri ABCD e A’B’C’D’ seguenti: A(1;6), B(3;5), C(3;8),
D(1;8), A’(6;1), B’(7;3), C’(4;3), D’(4;1).
g) I due quadrilateri sono simmetrici? ______ Ti sembra che ci possa essere un movimento che
porta ABCD in A’B’C’D’? Di che tipo? _______________________________________
Cerca di capire come potresti costruirlo.
h) Disegna i quadrilateri ABCD di vertici A(1;-1), B(3;0), C(3;2), D(1;3) e il quadrilatero A’B’C’D’ di
vertici A’(-1;0), B’(-3;-1), C’(-3;-3), D’(-1;-4).
i) Cerca di trovare il centro di simmetria in modo da trasformare il quadrilatero ABCD nel
quadrilatero A’B’C’D’. Ricorda che il centro di simmetria deve essere ___________ del
segmento che unisce due punti corrispondenti.
j) Verifica che il punto che hai trovato è veramente il centro di simmetria. Come lo verifichi? ___
_________________________________________________________________
k) Disegna il quadrilatero ABCD del punto a) ed il quadrilatero A’B’C’D’ di vertici A’(-2;-2), B’(-4;1), C’(-5;2), D’(-3;1).
l) Cerca di trovare il vettore che caratterizza la traslazione che porta il quadrilatero ABCD nel
quadrilatero A’B’C’D’.
Scrivi sul quaderno i procedimenti che puoi usare per trovare:
a. l’asse di simmetria, date due figure corrispondenti;
b. il centro di simmetria, date due figure corrispondenti;
c. il vettore della traslazione, date due figure corrispondenti;
d. il centro di rotazione e il rispettivo angolo.
Esercizio: individua tutte le possibili isometrie che fanno corrispondere al triangolo di vertici A(-4;2), B(-1;-2), P(1;0) il triangolo P(1;0), B’(4;0), C’(6;2).
13
Scheda 14 (Bis)
LE SIMMETRIE INTORNO A NOI
Obiettivi:
• Osservare come le isometrie sono presenti nella realtà intorno a noi;
• Saper costruire un fregio componendo varie trasformazioni;
• Saper eliminare le rotture di simmetrie.
In natura si possono individuare forme geometriche generate tra trasformazioni simmetriche; le
più frequenti sono la simmetria centrale e la simmetria assiale, presenti in natura nelle forme più
elementari come i cristalli di neve, i fiori, le piante e nell’arte. Sin dall’antichità, infatti, le
trasformazioni isometriche del piano sono state usate per creare fregi ornamentali e
pavimentazioni, per decorare soffitti e pareti di palazzi, per disegnare tessuti, per costruire rosoni
ed edifici monumentali, per realizzare statue.
Fiocchi di neve
Rosoni
Fregi
Esecuzione:
a) Considera l’immagine priva di simmetrie Motivo di partenza.jpg.
b) Attraverso il comando “Inserisci immagine” inserisci Motivo di partenza.jpg.
c) Utilizzando la traslazione, la simmetria centrale e la rotazione prova a costruire il tuo fregio.
Esegui anche sul quaderno, o su questa scheda, la costruzione realizzata al computer usando gli
strumenti della geometria (squadrette, righello, compasso, goniometro).
d) Che cosa hai ottenuto?
_________________________________________________________________
e) Quali trasformazioni hai utilizzato? In quale ordine?
_________________________________________________________________
f) Sei riuscito a “comporre” delle trasformazioni? ___________ Quali?
_________________________________________________________________
g) Considera l’immagine priva di simmetria Maschera 1.jpg.
h) Saresti capace di costruire una maschera simmetrica? Come faresti?
_________________________________________________________________
i) Attraverso il comando “Inserisci immagine” inserisci le immagini Maschera 1 dx.jpg e
Maschera 1 sx.jpg.
j) Considera una retta verticale alle due immagini e prova a costruire una maschera simmetrica.
k) Prova a cercare altre immagini non simmetriche e prova a costruire le necessarie simmetrie.
14
Scheda 14
LE SIMMETRIE INTORNO A NOI
Obiettivi:
• Osservare come le isometrie sono presenti nella realtà intorno a noi;
• Studiare i vari tipi di fregi;
• Dimostrare che esistono solo sette tipi di fregi.
Lavoro sul campo:
muniti di una macchina fotografica, girare per le strade della città e scoprire vari tipi di fregi
(osservare case, cancelli, chiese, strade…..);
per ogni fregio, scrivere la strada in cui è stato trovato (indirizzo preciso) e il luogo (casa,
cancello, chiesa, strada…..);
Lavoro a scuola:
stampare le foto;
preparare cartelloni.
Lavoro a casa:
leggere l’articolo “Alla caccia dei fregi” (su X la tangente, num. 12 novembre 2008) e farne un
riassunto.
Lavoro in laboratorio:
dimostrare che esistono solo sette tipi di fregi.
Esecuzione:
1) Nel piano cartesiano prendere una striscia di larghezza fissata e disegnare una retta r
esattamente a metà della striscia.
2) Disegna un motivo elementare (una bandierina per esempio) nella metà superiore della striscia
(vedere articolo).
3) Esegui sul motivo, ogni volta ripartendo dall’inizio, le seguenti isometrie:
a. traslare il motivo nella direzione r della striscia; il modulo del vettore traslazione è la
larghezza del motivo
b. eseguire una simmetria con asse perpendicolare ad r (per esempio l’asta della
bandierina); di seguito traslare il motivo ottenuto, con modulo pari alla sua larghezza
c. traslare il motivo nella direzione r della striscia ( il modulo del vettore traslazione è la
larghezza del motivo come in a)); successivamente ribaltare il disegno rispetto alla retta
r
d. in successione, ribaltare rispetto ad r e traslare come in a); ripetere il procedimento
(ribaltamento e traslazione), colorare di rosso i motivi “dispari” (cioè il primo, il terzo, il
quinto….). Il fregio è solo la parte rossa
e. ribaltare il motivo rispetto ad una retta perpendicolare ad r, ribaltare quanto ottenuto
rispetto ad r, traslare il tutto con modulo pari all’ampiezza del motivo finale
f. ribaltare il motivo rispetto ad una retta perpendicolare ad r (questo è il motivo “base”),
ribaltare quanto ottenuto rispetto ad r, traslare quest’ultimo con modulo pari alla sua
ampiezza; continuare a ribaltare rispetto ad r e poi traslare; colorare di rosso solo i
motivi base “dispari”. Il fregio è solo la parte rossa
g. eseguire una simmetria centrale del motivo, rispetto al punto “base” dell’asta della
bandierina; traslare il motivo ottenuto con modulo pari alla sua ampiezza.
Tutti questi fregi sono costruiti usando le isometrie. Con queste sette costruzioni abbiamo realizzato TUTTI gli schemi possibili di fregio.
15
4) Per convincertene, esegui questo ragionamento:
a. le traslazioni possono essere eseguite solo nella direzione di r. Perché? Cosa accadrebbe
se si andasse lungo un’altra direzione? (Ricorda che il fregio è una striscia e, quindi,
limitato in altezza)
____________________________________________________________
____________________________________________________________
b. le simmetrie assiali sono possibili solo con asse r oppure con assi perpendicolari ad r.
Perché? ______________________________________________________
____________________________________________________________
Prova a fare un esempio di una simmetria con asse “obliquo”.
c. possono esserci rotazioni diverse da quella di 180°? Perché?
____________________________________________________________
____________________________________________________________
16
I FREGI POSSIBILI
Per costruire un fregio, prendiamo una striscia di larghezza fissata e vediamo in quanti
modi un motivo elementare può ripetersi a intervalli uguali lungo di essa. Consideriamo
questo motivo elementare:
1) Il fregio più semplice lo otteniamo traslando successivamente questo elemento nella direzione del vettore v:
2) Possiamo eseguire una traslazione e una
successiva simmetria rispetto ad una retta
perpendicolare al vettore v:
3) Possiamo operare con una traslazione e una
simmetria della striscia rispetto alla direzione di v:
4) Eseguiamo ora una traslazione, poi una simmetria dell’elemento traslato rispetto al vettore
v, seguita da una ulteriore traslazione:
17
5) Eseguiamo una traslazione, una simmetria
rispetto alla direzione v e infine simmetrie rispetto ad assi perpendicolari a v:
6) Come nel caso 4, ma con l’aggiunta di
simmetrie rispetto ad assi perpendicolari alla
direzione v, otteniamo (completa tu)
________________________________
7) Con una traslazione e una simmetria centrale
cioè una rotazione di 180° otteniamo (completa tu)
___________________________________
Tutti questi fregi sono quindi costruiti utilizzando le isometrie. Con queste sette costruzioni, abbiamo realizzato tutti gli schemi possibili di fregio.
[da Leggere di Matematica su “Il nuovo format” di Maraschini-Palma]
18
I FREGI INTORNO A NOI
“In matematica si usa la parola fregio per indicare una figura piana che si ripete periodicamente in una sola direzione, cioè una figura piana il cui gruppo di simmetria (ovvero
l’insieme di quelle trasformazioni del piano che lasciano invariate le distanze e mutano la
figura in se stessa) contiene sì delle traslazioni, ma solo traslazioni in un’unica direzione e
tutte multiple di una traslazione base. Se vi guardate intorno, vi accorgerete facilmente che
siete circondati da fregi: non solo le decorazioni sulle facciate delle case, i giochi delle finestre dei grandi edifici, le balconate, le ringhiere in ferro battuto, ma anche le greche sui
quaderni dei bambini, le arcate cieche sulle chiese romaniche, le erlature dei castelli, i nastri che comprate in merceria, le orme lasciate sulla sabbia, …”
[da “Alla caccia dei fregi” su X la tangente, num. 12 novembre 2008]
Di seguito alcune fotografie scattate dagli studenti.
19
Scheda 15
INDIVIDUARE ASSI E CENTRI DI SIMMETRIA DI POLIGONI
Obiettivi:
• Saper individuare assi e centri di simmetria di poligoni
• Classificare i poligoni in base ai loro assi e centri di simmetria
Esecuzione:
a) Considera un triangolo: quanti assi di simmetria può avere? ________________________
b) Classifica i triangoli in base al numero di assi di simmetria:
0 assi:_____________________________________________________________
1 asse:_____________________________________________________________
2 assi:_____________________________________________________________
3 assi:_____________________________________________________________
c) Considera un quadrilatero: quanti assi di simmetria può avere?______________________
d) Classifica i quadrilateri in base al numero di assi di simmetria:
0 assi:_____________________________________________________________
1 asse:_____________________________________________________________
2 assi:_____________________________________________________________
3 assi:_____________________________________________________________
4 assi:_____________________________________________________________
e) Considera adesso un poligono con almeno 5 lati: esistono poligono di questo tipo con assi di
simmetria? Fai degli esempi: _____________________________________________
_________________________________________________________________
_________________________________________________________________
f) Proprietà: per ogni tipo di triangolo o quadrilatero individuato ai punti b) e d) scrivi le
proprietà che lo caratterizza:
g) Analizzare le figure esaminate precedentemente e scoprire se possiedono un centro di
simmetria:
Triangoli:
20
Quadrilateri:
Poligoni con almeno 5 lati:
21
Scheda 16
APPROFONDIMENTI: CONGRUENZA
Obiettivi:
• Approfondire il concetto di congruenza di figure piane
• Individuare i criteri di congruenza per i triangoli
• Modificare i criteri di congruenza per i triangoli nel caso di triangoli rettangoli
Esecuzione:
a) Rileggi la scheda 03.
b) Che cosa significa che due figure sono “congruenti”? Cerca la definizione sul libro.
_________________________________________________________________
_________________________________________________________________
c) Secondo te, si potrebbero dare altre definizioni di congruenza, utilizzando le isometrie?
_________________________________________________________________
_________________________________________________________________
d) Esistono criteri per verificare la congruenza di due figure, conoscendo solo alcuni “dati”?
Provare con i triangoli.
Disegnare al computer due triangoli con solo due elementi uguali (due lati, due angoli, un lato e
un angolo) e completare i triangoli con gli altri elementi che mancano a piacere. I due triangoli
sono uguali? __________________________________________________
Disegnare al computer due triangoli con solo tre elementi uguali (tre lati, tre angoli, due lati e
l’angolo compreso fra essi, due lati e un angolo non compreso fra essi, due angoli e un lato
(compreso o no fra gli angoli uguali)) e completare i triangoli con gli altri elementi che
mancano a piacere. I due triangoli sono uguali? Sempre? Distinguere i casi.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
e) Cerca sul libro i criteri di congruenza dei triangoli e verifica le tue conclusioni.
I criterio:
II criterio:
22
III criterio:
f) Secondo te, se i triangoli sono rettangoli come si possono modificare i criteri precedenti?
23
Scheda 17
APPROFONDIMENTI: PARALLELISMO
Obiettivi:
• Approfondire il concetto di parallelismo
• Individuare condizioni necessarie e sufficienti per individuare rette parallele
Esecuzione:
a) Cercare la definizione di rette parallele ______________________________________
_________________________________________________________________
b) Provare a dare altre definizioni di rette parallele, usando le isometrie (aiutati con le schede
precedenti):
c) Disegnare due rette parallele r ed s e una terza rette t che le taglia entrambe.
d) Misurare i quattro angoli che la retta t forma con la retta r e con la retta s. Che cosa noti?
_________________________________________________________________
_________________________________________________________________
e) Cerca sul libro i nomi degli angoli trovati:
f) Disegnare ora due rette non parallele r ed s e una terza rette t che le taglia entrambe.
g) Misurare i quattro angoli che la retta t forma con la retta r e con la retta s. Che cosa noti?
_________________________________________________________________
24
_________________________________________________________________
h) Puoi enunciare la condizione “necessaria” per il parallelismo di due rette:
se due rette sono parallele, allora tagliate da una trasversale formano angoli
____________________________________________________
i) Sarà vero il viceversa? Prova a disegnare due rette tagliate da una trasversale in modo che, per
esempio, due angoli alterni siano uguali.
j) Clicca su “Relazione fra due oggetti” e poi sulle due rette. Che cosa osservi?
_________________________________________________________________
k) Prova con gli altri tipi di angoli e fai le tue osservazioni.
_________________________________________________________________
_________________________________________________________________
l)
Puoi enunciare la condizione “sufficiente” per il parallelismo di due rette:
se due rette tagliate da una trasversale formano angoli ________________
______________________________ allora le due rette sono parallele.
25
Scheda 18
LA SIMMETRIA COME ISOMETRIA FONDAMENTALE
Obiettivi:
• Studiare la composizione di simmetrie assiali
• Dimostrare che ogni isometria si ottiene come prodotto di simmetrie assiali
Esecuzione:
Comporre due isometrie significa effettuarle in successione
a) Disegna un triangolo ed effettua su di esso in successione due diverse isometrie fra quelle
studiate precedentemente. Ripeti il procedimento 5 volte, stampando il risultato, specificando
le isometrie che sono state usate.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
b) Prova adesso ad effettuare le stesse isometrie, però in ordine inverso. Ottieni lo stesso
risultato? __________________________________________________________
La composizione di due isometrie si chiama anche prodotto delle isometrie.
Da quanto visto prima, puoi dire che il prodotto di due isometrie è commutativo? _________
Composizione di due simmetrie assiali.
c)
d)
e)
f)
Disegna un triangolo qualsiasi ABC.
Usando il comando “Retta per due punti” disegna una retta e assegnale il nome r.
Trova il simmetrico del triangolo ABC nella simmetria di asse r ed assegnagli il nome A’B’C’.
Trova adesso il simmetrico del triangolo A’B’C’ nella simmetria di asse r ed assegnagli il nome
A’’B’’C’’.
g) Che relazione c’è tra il triangolo ABC ed il triangolo A’’B’’C’’? _______________________
Puoi concludere che:
componendo due simmetrie assiali con lo stesso asse ____________________
_________________________________________________________
h)
i)
j)
k)
l)
Disegna un triangolo qualsiasi ABC.
Usando il comando “Retta per due punti” disegna una retta e assegnale il nome r.
Disegna una retta parallela alla retta r ed assegnale il nome s.
Trova il simmetrico del triangolo ABC nella simmetria di asse r ed assegnagli il nome A’B’C’.
Trova adesso il simmetrico del triangolo A’B’C’ nella simmetria di asse s ed assegnagli il nome
A’’B’’C’’.
m) Che relazione c’è tra il triangolo ABC ed il triangolo A’’B’’C’’? _______________________
n) Sai individuare una isometria che porta il triangolo ABC nel triangolo A’’B’’C’’? Spiega quale
potrebbe essere e fai la verifica al computer.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
26
Puoi concludere che:
componendo due simmetrie assiali con assi paralleli otteniamo ________
____________________________________________________
o)
p)
q)
r)
s)
Disegna un triangolo qualsiasi ABC.
Usando il comando “Retta per due punti” disegna una retta e assegnale il nome r.
Disegna una retta perpendicolare alla retta r ed assegnale il nome s.
Trova il simmetrico del triangolo ABC nella simmetria di asse r ed assegnagli il nome A’B’C’.
Trova adesso il simmetrico del triangolo A’B’C’ nella simmetria di asse s ed assegnagli il nome
A’’B’’C’’.
t) Che relazione c’è tra il triangolo ABC ed il triangolo A’’B’’C’’? _______________________
u) Sai individuare una isometria che porta il triangolo ABC nel triangolo A’’B’’C’’? Spiega quale
potrebbe essere e fai la verifica al computer.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
Puoi concludere che:
componendo due simmetrie assiali con assi perpendicolari otteniamo __________
__________________________________________________________
v)
w)
x)
y)
z)
Disegna un triangolo qualsiasi ABC.
Usando il comando “Retta per due punti” disegna una retta e assegnale il nome r.
Disegna una retta incidente, ma non perpendicolare alla retta r ed assegnale il nome s.
Trova il simmetrico del triangolo ABC nella simmetria di asse r ed assegnagli il nome A’B’C’.
Trova adesso il simmetrico del triangolo A’B’C’ nella simmetria di asse s ed assegnagli il nome
A’’B’’C’’.
aa) Che relazione c’è tra il triangolo ABC ed il triangolo A’’B’’C’’? _______________________
bb) Sai individuare una isometria che porta il triangolo ABC nel triangolo A’’B’’C’’? Spiega quale
potrebbe essere e fai la verifica al computer.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
Puoi concludere che:
componendo due simmetrie assiali con assi incidenti otteniamo ________________
____________________________________________________________
CONCLUSIONE
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
27
Scheda 19
LA SIMMETRIA COME ISOMETRIA FONDAMENTALE
Obiettivi:
• Studiare la composizione di simmetrie assiali
• Dimostrare che ogni isometria si ottiene come prodotto di simmetrie assiali
Esecuzione:
a)
b)
c)
d)
e)
Disegna un triangolo qualsiasi ABC.
Usando il comando “Retta per due punti” disegna una retta e assegnale il nome r.
Disegna due rette parallele alla retta r ed assegna loro il nome s e t.
Trova il simmetrico del triangolo ABC nella simmetria di asse r ed assegnagli il nome A’B’C’.
Trova adesso il simmetrico del triangolo A’B’C’ nella simmetria di asse s ed assegnagli il nome
A’’B’’C’’.
f) Trova adesso il simmetrico del triangolo A’’B’’C’’ nella simmetria di asse t ed assegnagli il nome
A’’’B’’’C’’’.
g) Che relazione c’è tra il triangolo ABC ed il triangolo A’’’B’’’C’’’? ______________________
h) Sai individuare una isometria che porta il triangolo ABC nel triangolo A’’’B’’’C’’’? Spiega quale
potrebbe essere e fai la verifica al computer.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
Puoi concludere che:
componendo tre simmetrie assiali con assi paralleli otteniamo ________________
___________________________________________________________
i) Disegna un triangolo qualsiasi ABC.
j) Usando il comando “Retta per due punti” disegna tre rette che si incontrano in uno stesso
punto e assegna loro il nome r, s e t. Chiama il punto di incontro O.
k) Trova il simmetrico del triangolo ABC nella simmetria di asse r ed assegnagli il nome A’B’C’.
l) Trova adesso il simmetrico del triangolo A’B’C’ nella simmetria di asse s ed assegnagli il nome
A’’B’’C’’.
m) Trova adesso il simmetrico del triangolo A’’B’’C’’ nella simmetria di asse t ed assegnagli il nome
A’’’B’’’C’’’.
n) Che relazione c’è tra il triangolo ABC ed il triangolo A’’’B’’’C’’’? ______________________
o) Sai individuare una isometria che porta il triangolo ABC nel triangolo A’’’B’’’C’’’? Spiega quale
potrebbe essere e fai la verifica al computer.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
Puoi concludere che:
componendo tre simmetrie assiali con assi incidenti nello stesso punto otteniamo _______
_______________________________________________________________
...ancora più difficile...
p) Disegna un triangolo qualsiasi ABC.
28
q) Usando il comando “Retta per due punti” disegna tre rette che si incontrano in tre punti diversi
e assegna loro il nome r, s e t.
r) Trova il simmetrico del triangolo ABC nella simmetria di asse r ed assegnagli il nome A’B’C’.
s) Trova adesso il simmetrico del triangolo A’B’C’ nella simmetria di asse s ed assegnagli il nome
A’’B’’C’’.
t) Trova adesso il simmetrico del triangolo A’’B’’C’’ nella simmetria di asse t ed assegnagli il nome
A’’’B’’’C’’’.
u) Che relazione c’è tra il triangolo ABC ed il triangolo A’’’B’’’C’’’? ______________________
v) Sai individuare una isometria che porta il triangolo ABC nel triangolo A’’’B’’’C’’’? Spiega quale
potrebbe essere e fai la verifica al computer.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
Puoi concludere che:
componendo tre simmetrie assiali con assi incidenti in punti distinti otteniamo _______
______________________________________________________________
w) Disegna un triangolo qualsiasi ABC.
x) Usando il comando “Retta per due punti” disegna tre rette di cui le prime due parallele e
assegna loro il nome r, s e t.
y) Trova il simmetrico del triangolo ABC nella simmetria di asse r ed assegnagli il nome A’B’C’.
z) Trova adesso il simmetrico del triangolo A’B’C’ nella simmetria di asse s ed assegnagli il nome
A’’B’’C’’.
aa) Trova adesso il simmetrico del triangolo A’’B’’C’’ nella simmetria di asse t ed assegnagli il nome
A’’’B’’’C’’’.
bb) Che relazione c’è tra il triangolo ABC ed il triangolo A’’’B’’’C’’’? ______________________
cc) Sai individuare una isometria che porta il triangolo ABC nel triangolo A’’’B’’’C’’’? Spiega quale
potrebbe essere e fai la verifica al computer.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
dd) Il risultato è lo stesso se le parallele sono s e t? Verifica. ___________________________
ee) Il movimento è lo stesso? _______________________________________________
Puoi concludere che:
componendo tre simmetrie assiali in cui soltanto due assi sono tra loro paralleli otteniamo
______________________________________________________________
29