Oscillazioni e Onde
Forza elastica
Riprendiamo la legge oraria di una massa attaccata a una molla vincolata in un
estremo. Per fare ciò occorre scriverne la legge del moto:
−kx = ma
− kx = m
d 2x
dt
2
da cui
d 2x
⇒
dt 2
k
=− x
m
Per trovare la legge oraria basta risolvere questa equazione differenziale:
d 2x
dt 2
=−
k
x = −ω 2 x
m
A. Romero
con
ω=
k
m
Scmat- Oscillazioni
2
d x(t)
2
+ ω x(t) = 0
2
dt
1
Forza elastica
E’ soddisfatta da una funzione la cui derivata seconda sia uguale alla funzione
stessa cambiata di segno, a meno del coefficiente di proporzionalità (k/m).
sen(ωt )
Tale funzione è del tipo
con
ω=
k
m
x ( t ) = Asen(ωt + φ)
Infatti se provo la soluzione :
v = dx / dt = ω A cos (ω t + φ )
velocità e accelerazione
sono
a = dv / dt = d x / dt = −ω Asen (ωt + φ )
2
2
2
a = − ω Asen (ω t + φ ) = − ω x
2
2
Quindi ho che soddisfo la
Equazione dell’oscillatore
armonico A. Romero
d 2 x
+ ω 2 x = 0
dt 2
Scmat- Oscillazioni
2
Equazione oscillatore armonico
Molti fenomeni descritti dalla legge dell’
oscillatore armonico (semplice, smorzato
o forzato)
Moto di un pendolo semplice
Moto di pendolo di torsione
Circuiti elettrico
Oscillazione di liquido in un cannello
Moto di molecole
A. Romero
Scmat- Oscillazioni
3
Forza elastica
La legge oraria è quindi:
x ( t ) = Asen
(ω t
+ φ)
Oppure (equivalenti seno
x ( t ) = A cos (ω t + φ )
e coseno, cambia φ ):
dove A è l'ampiezza di oscillazione con dimensioni lunghezza, e φ è la fase.
A e φ dipendono dalle condizioni iniziali del moto, ω dalla fisica (m e k)
T periodo tempo per
oscillazione completa di seno o
coseno cioè 2π
(ω ( T + t ) + φ ) → (ω t + φ + 2 π )
ωT = 2π ⇒ T = 2π / ω
T = 2π / ω
ν = 1/ T = ω/ 2π
si osserva che:
→ nel punto di massimo allungamento e di massima compressione,
l'accelerazione è massima e la velocità è nulla (il corpo sta infatti
invertendo il verso del moto)
→ nel punto di equilibrio, l'accelerazione è nulla e la velocità massima
(con segno a seconda che la molla si stia allungando o comprimendo)
A. Romero
Scmat- Oscillazioni
4
Moto Periodico
Moto periodico con pulsazione
x ( t ) = A sin( ω t )
v( t ) = Aω cos( ωt )
a(t ) = − Aω sin( ωt )
2
A. Romero
Scmat- Oscillazioni
ω=
2π
,ϕ = 0
T
(posizione)
(velocità)
(accelerazione)
5
v0
x
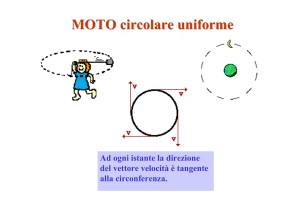
La figura mostra una particella che si muove lungo
una circonferenza di raggio A con velocità costante
v0. Anche la sua velocità angolare ω è costante ed è
legata alla velocità lineare dalla relazione v0 = Aω
Poiché la particella percorre uno spazio 2πA
durante un giro, il periodo e la frequenza del moto
circolare si ricavano da:
v 0 T = 2π A →
T=
ν =
2 π A 2π
=
v0
ω
1 ω
=
T 2π
Se la particella parte all’istante t = 0 sull’asse x, il suo spostamento angolare in
un istante successivo è dato da θ = ωt = 2πνt.
Dalla figura si può vedere che la componente x della posizione della particella è
data da:
x = A cosθ
θ = A cos2πν
πνt
πν
1
che è uguale all’espressione per il moto armonico semplice.
A. Romero
Scmat- Oscillazioni
6
Energia nel moto armonico semplice
Quando un corpo attaccato ad una molla oscilla, esso ha energia cinetica ed
energia potenziale, che variano entrambe nel tempo; ma la loro somma, che è
l’energia totale, è costante. Infatti
L’energia potenziale Ep di una molla di costante elastica K, allungata di un
tratto x dalla posizione di equilibrio, è data dall’equazione
Ep = ½ kx2
E p = 1/ 2kA2sen2 (ωt )
L’energia cinetica è:
Ec = ½ mv2 L’energia
totale
E c = 1 / 2m ω 2 A 2 cos 2 ( ω t ) = 1 / 2kA 2 cos 2 ( ω t )
è
la
somma
di
queste
due
quantità:
Etot = ½ kx2 + ½ mv2=
½ k A2 infatti sen2 +cos2=1
L’energia totale di un corpo che oscilla con moto armonico semplice è
direttamente proporzionale al quadrato dell’ampiezza.
A. Romero
Scmat- Oscillazioni
7
Energia del moto armonico
A. Romero
Scmat- Oscillazioni
8
Moto Periodico Composto
Due corpi identici attaccati a molle identiche vengono lasciati andare
simultaneamente. Essi raggiungono le loro posizioni di equilibrio nello stesso
istante, perché il periodo dipende dalla massa e dalla costante elastica, che sono le
stesse, e non dall’ampiezza.
Grafici dello spostamento
In funzione del tempo per
i due corpi. Le cose
cambiano se le fasi
iniziali non sono le stesse
A. Romero
Scmat- Oscillazioni
9
Composizione di moti armonici su stesso asse
Se ho due moti armonici con stessa
pulsazione posso scrivere la loro somma
come un moto armonico di stessa
pulsazione, fase diversa e ampiezza che
dipende da differenza di fase :
x 1 ( t ) = A 1 sen (ω t + ϕ 1 )
x 2 ( t ) = A 2 sen (ω t + ϕ 2 )
x ( t ) = x 1 ( t ) + x 2 ( t ) = Asen (ωt + ψ )
per dimostrarlo posso usare il metodi di Fresnel ( v grafico precedente) o
quello qui indicato. Esplicito il seno della somma
x ( t ) = A 1 (sen ω t ⋅ cos ϕ 1 + cos ω t ⋅ sen ϕ 1 ) +
A 2 (sen ω t ⋅ cos ϕ 2 + cos ω t ⋅ sen ϕ 2 )
Raccolgo a fattor comune seno e coseno
x ( t ) = (A 1 cos ϕ 1 + A 2 cos ϕ 2 )sen ω t + (A 1sen ϕ 1 + A 2 sen ϕ 2 ) cos ω t
A. Romero
Scmat- Oscillazioni
10
Composizione di moti armonici su stesso asse(cont)
Se pongo
A cos ψ = (A 1 cos ϕ 1 + A 2 cos ϕ 2 )
Asen ψ = (A 1sen ϕ 1 + A 2 sen ϕ 2 )
Quadrando e sommando ottengo
A = A12 + A 22 + 2A1A 2 cos(ϕ1 − ϕ2 )
A è massima se i moti hanno stessa fase , minima se fasi differiscono di π
tg ψ =
A 1sen ϕ 1 + A 2 sen ϕ 2
A 1 cos ϕ 1 + A 2 cos ϕ 2
Ottengo un moto armonico con ampiezza dipendente da differenza di fase
x ( t ) = x 1 ( t ) + x 2 ( t ) = Asen (ω t + ψ )
A. Romero
Scmat- Oscillazioni
11
Somma di due moti armonici lungo la stessa direzione con stessa ampiezza per
vari valori della differenza di fase
A. Romero
Scmat- Oscillazioni
12
6
y(t)
5
4
3
3
2
2
1
1
0
-2
-3
T
T
T/
2
0
T
T
-1
3/
4
-2
t
3/
4
T/
2
0
T/
4
0
-1
t
-3
-4
-4
-5
-5
-6
-6
∆ϕ =3/2π
6
Se si considerano due segnali sinusoidali aventi
la stessa pulsazioni, si può poi parlare di
differenza di fase tra loro ∆φ o sfasamento.
5
4
3
2
1
T
T
3/
4
-2
T/
2
-1
T/
4
0
0
y(t)
∆ϕ =π
5
∆ϕ =π/2
4
6
T/
4
y(t)
Differenza di fase di onde sinusoidali
t
y 2 (t ) = A ⋅ sen(ωt + ϕ2 )
-3
-4
-5
∆ϕ = ϕ 2 − ϕ1
-6
A. Romero
y1 (t ) = A ⋅ sen(ωt + ϕ1 )
Scmat- Oscillazioni
13
8
7
6
5
4
3
2
1
0
-1
-2
-3
-4
-5
-6
-7
-8
∆ϕ =π/2
T
T
3/
4
T/
2
T/
4
y(t)
Somma
0
t
6
4
3
2
1
0
6
∆ϕ =π
5
T
T
3/
4
-2
t
T/
2
0
-1
-3
4
-4
3
-5
2
-6
1
T
T
t
3/
4
-2
T/
2
-1
T/
4
0
0
y(t)
∆ϕ =7/8π
5
T/
4
y(t)
Somma di due onde non in fase
-3
-4
Somma
-5
-6
A. Romero
Scmat- Oscillazioni
14
Composizione di moti armonici se ho forze diverse
Se ho due moti armonici con diversa pulsazione
(soggetti a due forze diverse) ho due diverse x 1 ( t ) = A 1 sen (ω 1 t + ϕ 1 )
equazioni differenziali .
x 2 ( t ) = A 2 sen (ω 2 t + ϕ 2 )
x =x1+x2 non è soluzione di nessuna delle due
Per sommare uso le formule di Fresnel e ho:
δ = δ 1 + δ 2 = (ω 1 t + ϕ 1 ) - (ω 2 t + ϕ 2 ) 1 = ( ω 1 − ω 2 ) t + ϕ 1 − ϕ 2
A ( t ) = A12 + A 22 + 2A1A 2 cos[(ω1 − ω2 ) t + (ϕ1 − ϕ 2 )]
Moto non è armonico semplice: ampiezza è funzione del tempo modulata: ad
esempio se A1 = A2 = A e φ1= φ2 = 0
x ( t ) = x 1 ( t ) + x 2 ( t ) = Asenω1 t + Asenω2 t = 2A cos
ω1 − ω2
ω + ω2
t sen 1
t
2
2
E ottengo
A. Romero
Scmat- Oscillazioni
15
Composizione di moti armonici se ho forze diverse
x ( t ) = A ( t ) sen ω t = 2 A cos Ω t sen ω t
Se pongo
ω1 + ω2
ω=
2
ω1 − ω2
Ω=
2
Moto non è armonico semplice: ampiezza è funzione del tempo o modulata.
Fenomeno è detto Battimento è sfruttato nelle trasmissioni radio AM ω è
pulsazione di onda radio e Ω pulsazione generata nel microfono
A. Romero
Scmat- Oscillazioni
16
Composizione di moti armonici su asse perpendicolari
Se ho punto soggetto a due forze elastiche in
direzioni ortogonali. Ho sovrapposizione di due
moti armonici rettilinei che danno moto piano .
Supponiamo siano con stessa costante elastica
quindi stessa pulsazione
x ( t ) = A sen ω t
y ( t ) = B sen ( ω t + ϕ )
Se sono in fase e φ=0
x ( t ) = A sen ω t , y ( t ) = B sen ω t
x A
= ⇒ retta
y B
retta fa angolo θ con asse x. Simile se φ=π
x
A
= − ⇒ retta
y
B
A. Romero
Scmat- Oscillazioni
17
Composizione di moti armonici su asse perpendicolari
Se sono in
φ=π/2
quadratura di fase e
x ( t ) = A sen ω t
π
y ( t ) = B sen ( ω t + ) = B c os ω t
2
x 2 y2
2
2
+
=
(cos
ω
t
+
s
en
ωt ) = 1
2
2
A B
Ellisse percorsa in senso orario (antiorario se φ=3π/2) .
Se A=B cerchio
Queste figure si possono osservare con oscilloscopio. In
situazioni particolari ellisse degenera in cerchi o in rette. In
onde EM utilizzati per studio di polarizzazione
A. Romero
Scmat- Oscillazioni
18
A. Romero
Scmat- Oscillazioni
19
Figura di Lissajous
Una Figura di Lissajous è il grafico di una curva data
dal sistema di equazioni parametriche:
x = A x cos( ωx t + δ x )
y = A y cos( ωy t + δ y )
dove Ai sono le ampiezze, le ωi le pulsazioni e le φi le
fasi di due moti oscillatori ortogonali.
Esistono delle figure particolari per
determinati valori del rapporto ωx e
ωy
della differenza di fase ∆δ.
Esprimendo le due equazioni come:
x = A x cos( ωt + δ )
y = A y sent
si ottengono le figure di Lissajous qui
mostrate per i diversi valori di ω e δ
A. Romero
Scmat- Oscillazioni
20
oscillatore armonico smorzato da
forza di attrito
Un oscillatore armonico nella realtà dopo un certo numero di oscillazioni si ferma
Se il corpo è soggetto alla forza di attrito radente di modulo F=µ mg sempre in
direzione opposta al moto, compie oscillazioni sempre più piccole ( fa meno strada
per attrito) . La figura da l’idea di cosa succede
:
Il periodo è uno pseudoperiodo
in quanto il moto non è armonico
semplice
A. Romero
Scmat- Oscillazioni
21
oscillatore armonico smorzato da
forza viscosa
Riprendiamo il problema di una massa attaccata a una molla vincolata in un
estremo e soggetta anche a una forza di attrito viscoso: la legge del moto diventa :
− kx − λ v = ma
da cui
dx
d2x
− kx − λ = m 2 ⇒
dt
dt
Se pongo
γ=
d 2 x λ dx k
+
+ x=0
2
dt m dt m
λ
k
e ω0 =
2m
m
Ho l’equazione dell’oscillatore
armonico smorzato
2
d x(t)
dx
2
+ 2γ + ω x (t ) = 0
2
dt
dt
0
A. Romero
Scmat- Oscillazioni
22
oscillatore armonico smorzato
αt
Cerco soluzione del tipo
x=e
Sostituisco
d 2 ( e αt )
d ( e αt )
2
αt
2
+
γ
+
ω
(
e
)=0
2
dt
dt
e ottengo
0
e (α + 2 γα + ω0 ) = 0
αt
2
2
Il prodotto = 0 se parentesi è nulla (esponenziale sempre diverso da
zero). Ho equazioni di 20 grado in α con soluzioni
α = − γ ± γ 2 − ω02
A. Romero
Ho tre casi possibili a cui corrispondono
soluzioni diverse, che dipendono dalle relazioni
tra i parametri fisici dell’oscillatore
Scmat- Oscillazioni
23
Smorzamento forte
Se
γ > ω0
2
2
λ2 > 4 m k
Quindi
α ha due distinti valori ambedue negativi
α1 = − γ + γ 2 − ω02 ; α 2 = − γ − γ 2 − ω02
La soluzione generale è una combinazione lineare delle due ed è un
esponenziale decrescente , A e B sono determinate dalle condizioni iniziali
x ( t ) = Ae + Be = e (Ae
α1t
A. Romero
α2t
− γt
t γ 2 −ω02
Scmat- Oscillazioni
+ Be
− t γ 2 −ω02
)
24
Smorzamento critico
Se
γ = ω0
2
2
α ha due soluzioni coincidenti
λ2 = 4 m k
Quindi
α1 = α 2 = − γ
La soluzione generale è ancora un esponenziale decrescente
x ( t ) = e − γt (At + B)
A. Romero
Scmat- Oscillazioni
25
Smorzamento debole
Se
γ 2 < ω02
Quindi
λ2 < 4 m k
Soluzioni per α sono valori complessi e coniugati
α1 = − γ + i ω02 − γ 2 = − γ + iω;
α 2 = − γ − i ω02 − γ 2 = − γ − iω
La soluzione generale è una combinazione lineare delle due, A e B sono determinate
dalle condizioni iniziali
x ( t ) = Ae + Be = e (Ae + Be )
α1t
α2t
− γt
iωt
− iωt
Utilizzando la formula di Eulero si arriva alla soluzione
x ( t ) = A 0 e sen(ωt + ϕ)
− γt
con ω = ω02 − γ 2 < ω0
A. Romero
Scmat- Oscillazioni
26
Oscillatore forzato
Riassumendo quanto visto finora il punto materiale, soggetto a forza elastica e ad
attrito costante o viscoso, compie oscillazioni libere che si smorzano
velocemente (ad esempio acqua in un bicchiere, pendolo senza molla, etc)
Se si vogliono oscillazioni permanenti con ampiezza A e pulsazione ω
costanti applico una forza sinusoidale di pulsazione ω diversa da quella propria
ω0 per cui l’equazione del moto diventa :
ma = − kx − λv + F0senωt
d2x
dx
F0
2
+ 2 γ + ω0 x = sen ωt
2
dt
dt
m
A. Romero
Scmat- Oscillazioni
27
Oscillatore forzato
Se
l’equazione sopra scritta
ammette, come vedremo,
una
soluzione particolare del tipo
x ( t ) = Asen(ωt + φ)
la soluzione generale è una combinazione lineare di questa e della soluzione
dell’omogenea associata quindi del tipo
x ( t ) = Asen(ωt + φ) + ae α t + be α t
1
2
Il moto totale è la somma di due moti: uno oscillante smorzato con una certa
pulsazione ω0 (quella dell'oscillatore smorzato) ed uno oscillante di ampiezza costante
alla
pulsazione
propria
della
forza
esterna
ω2.
Il sistema ha dunque un transiente oscillante iniziale che svanisce esponenzialmente
col tempo, lasciando il posto ad un'oscillazione pura ad ampiezza costante; questa
oscillazione è determinata essenzialmente dalla forza esterna, e presenta uno
sfasamento con essa.
A. Romero
Scmat- Oscillazioni
28
Oscillatore forzato
ma = −kx − λv + F0senωt
Se nell’equazione
provo a sostituire
del
moto
x ( t ) = Asen(ωt + φ)
ottengo
F0
− ω Asen(ωt + φ) + 2 γωA cos(ωt + φ) + ω Asen(ωt + φ) = senωt
m
2
2
0
Sviluppo seno e coseno di somma , raccolgo senωt e cosωt e ottengo che deve
essere :
A=
F0
1
m (ω02 − ω2 ) 2 + 4 γ 2 ω2
2 γω
tgφ = − 2
ω0 − ω 2
Ho moto armonico con pulsazione diversa da quella propria, posizione sfasata
di φ rispetto alla forza F, A e φ dipendono dalla dinamica e non dalle
condizioni iniziali
A. Romero
Scmat- Oscillazioni
29
Oscillatore forzato: risposta in funzione di ω
1) Se ω<< ω0
A=
F0
1
F0
F0
≈
=
m (ω02 − ω2 ) 2 + 4 γ 2 ω2 mω02 k
tgφ = −
k, costante elastica è il parametro più
importante :
2) Se ω>> ω0
x è in opposizione di fase con la
forza , massa è parametro
importante
2 γω
≈0⇒φ≈0
2
2
ω0 − ω
x≈
A=
F0
senωt
k
F0
1
F0
≈
m (ω02 − ω2 ) 2 + 4 γ 2 ω2 mω2
tgφ = −
x≈
A. Romero
x è in fase con la forza
Scmat- Oscillazioni
2 γω
⇒φ≈π
2
2
ω0 − ω
F0
sen (ωt + π)
2
mω
30
Oscillatore forzato: risposta in funzione di ω
A=
3) Se ω= ω0
F0
1
F0
≈
m (ω02 − ω2 ) 2 + 4 γ 2 ω2 2mγω0
tgφ = −
γ coeff. Smorzamento è il parametro
più importante: ho risonanza :
x≈
2 γω
π
≈
∞
⇒
φ
≈
ω02 − ω2
2
F0
cos ωt
2mγω 0
x è in quadratura di
fase con la forza
Se voglio la A massima
azzero dA/d ω e ottengo
ω = ωM = ω02 − 2 γ 2 < ω0
A ( ωM ) =
F0
1
> A ( ω0 )
2
2
2mγ (ω0 − 2 γ
A. Romero
Scmat- Oscillazioni
K, costante elastica è il parametro più importante :
31
Potenza media fornita
La potenzia media fornita da forza
che fa muovere oscillatore
Pm = γmω2 A 2
se derivo la potenza media Pm rispetto a ω ho la potenza
media massima per ω= ω0
Pris ,m = γmω02 A 2ris
se derivo la potenza media Pm rispetto a ω ho la potenza media
massima per ω= ω0
A. Romero
Scmat- Oscillazioni
K, costante elastica è il parametro più importante :
32
Analisi di Fourier
Il moto armonico è importante perché tutti fenomeni che si ripetono dopo un
certo T possono essere studiati con l’analisi di Fourier.
Se abbiamo una f(t) periodica con periodo T e in tale tempo f(t) è divisibile in
intervalli di tempo in cui f(t) è continua e monotona possiamo esprimerla
come somma di infiniti moti armonici :
∞
f ( t ) = a 0 + ∑ m (a m sen mωt + b m cos mωt)
1
∞
f ( t ) = a 0 + ∑ m c m sen (mωt + ϕm )
1
I coefficenti dello sviluppo di Fourier am bm cm si calcolano da
2 T
2 T
a m = ∫0 f ( t ) sen mω t dt ; b m = ∫0 f ( t ) cos mω t dt
T
T
A. Romero
Scmat- Oscillazioni
33
Analisi di Fourier
am
c m = a m + b m ; tgϕ m =
bm
2
2
T è il periodo di f(t) e ω =2π/T , a0 è il valor medio di f(t) dato da
1 T
a 0 = ∫0 f ( t )dt
T
Termine con m=1 è il primo armonico e ha pulsazione ω
Termini con m>1 sono armonici superiori con pulsazioni 2 ω,3 ω, etc
La determinazione dei coefficienti am e bm è detta Analisi di
Fourier della f(t)
A. Romero
Scmat- Oscillazioni
34