Pendolo semplice

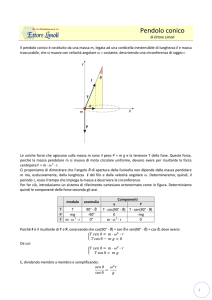
Pendolo semplice
Il pendolo semplice è formato da una massa puntiforme m sospesa ad un filo in estensibile di
lunghezza  . Studiamo le piccole oscillazioni del pendolo semplice in assenza di attriti.
Le forze agenti sul corpo puntiforme di massa m sono il peso mg e la tensione T. Quando la massa
m sia allontanata dalla posizione di equilibrio il pendolo inizia ad oscillare.
Per la II legge di Newton
 

mg  T  ma
Consideriamo le componenti lungo la traiettoria (orientata come in figura) e ortogonalmente alla
traiettoria
-mg sen  = m at (1)
T  mg cos   m aN
Il segno meno in (1) è dovuto al fatto che la forza ha segno opposto rispetto a quello della
coordinate sulla traiettoria.
d 2
v2
Poiché a t   2 ;
aN 

dt
Si ottiene
d 2
 gsen    2
(2)
dt
v2

mg
cos


m
T

Se << 1 radiante, sen ≈  e l’equazione (2) per le piccole oscillazioni diventa
d 2 g
(3)
 0
dt 2 
La (3) è un’equazione differenziale di II grado omogenea a coefficienti costanti. Una soluzione, che
rappresenta la legge oraria del moto armonico, è
= max cos (0t + )
g
è la pulsazione
0 
