Meccanica – sistema biella-manovella
Sistema biella-manovella
Esercizi
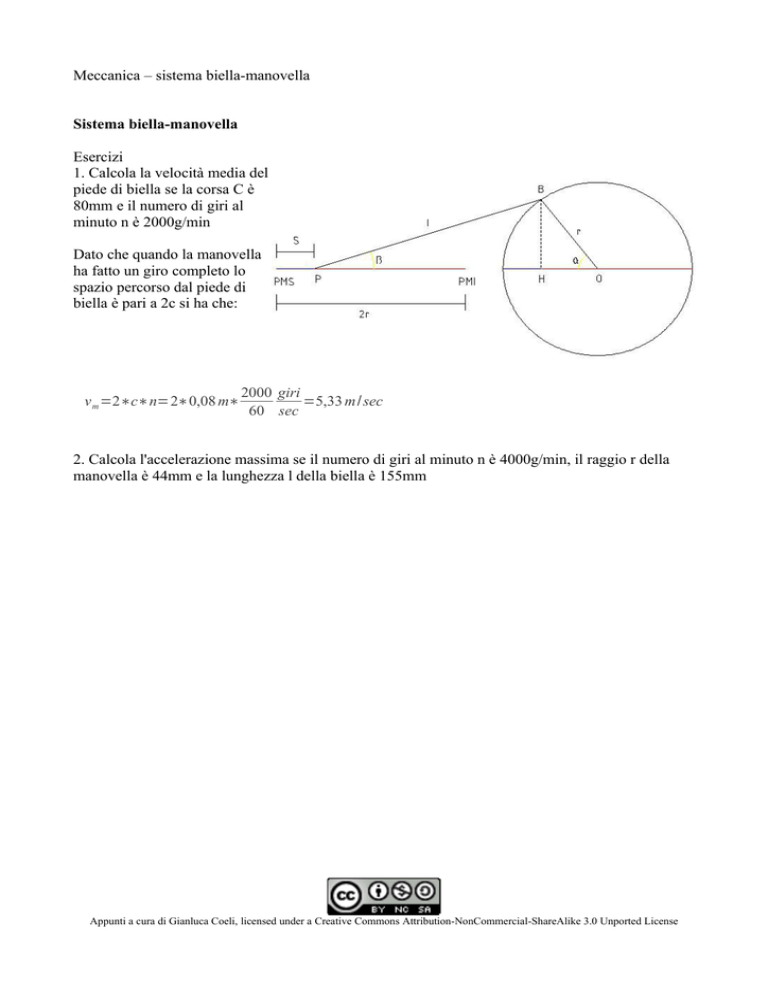
1. Calcola la velocità media del
piede di biella se la corsa C è
80mm e il numero di giri al
minuto n è 2000g/min
Dato che quando la manovella
ha fatto un giro completo lo
spazio percorso dal piede di
biella è pari a 2c si ha che:
v m =2∗c∗n=2∗0,08 m∗
2000 giri
=5,33 m/sec
60 sec
2. Calcola l'accelerazione massima se il numero di giri al minuto n è 4000g/min, il raggio r della
manovella è 44mm e la lunghezza l della biella è 155mm
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
Forza risultante che agisce sul
pistone
Forze alterne d'inerzia del 1 ordine:
F i=−m p a i è una forza che tende ad
opporsi alla variazione del moto in
atto.
Considero i quattro casi in figura:
dalla formula dell'accelerazione,
consideriamo il contributo solo
dell'armonica di primo ordine (dato che
quello dell'armonica di secondo ordine
è trascurabile perché piccolo):
2
a=ω r cos α
1° caso: andata → l'accelerazione
aumenta, verso dx
2° caso: andata → l'accelerazione
diminuisce, quindi verso sx
(decelerazione , perché al PMI il piede
di biella si ferma e cambia verso)
3° caso: ritorno → l'accelerazione
aumenta verso sx
4° caso: ritorno → l'accelerazione
diminuisce quindi vero dx
(decelerazione, perché al PMS il piede
di biella si ferma e cambia verso)
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
Il diagramma risultante, per l'accelerazione è:
ω2 r
-ω2 r
L'accelerazione su una massa, crea una forza
d'inerzia:
F⃗ i=−m∗⃗a
una forza, cioè, che ha la stessa direzione dell'accelerazione ma verso opposto (come si vede dalla
figura illustrante i 4 casi).
Vediamo il diagramma della Forza d'inerzia: si
ricava dal grafico dell'accelerazione visto sopra,
dove però, punto per punto, si cambia il segno
delle ordinate (le coordinate dell'asse y):
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
Se facciamo riferimento a un motore oleodinamico (quindi non a scoppio), le forze che agiscono sul
pistone, nella fase di andata e di ritorno, sono:
F andata= p∗A p
F ritorno= p∗( A p −As ) (cioè l'area del pistone,
che ha diametro D, meno l'area del cilindro con
diametro d)
Il grafico di queste forze è:
La forza risultante che agisce sul pistone (che
serve conoscere per dimensionare la biella e
stabilire i cavalli, cioè la potenza, del motore) si
ricava sommando, punto per punto, i diagrammi
della forza d'inerzia e della forza che agisce sul
pistone (tenendo conto che le ordinate
corrispondenti allo spostamento zero, sono, in
valore assoluto, uguali):
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License