ESAME DI STATO DI LICEO SCIENTIFICO
Sessione Ordinaria 2008
PIANO NAZIONALE INFORMATICA
Quesito 1
Siano dati un cono equilatero e la sfera in esso inscritta. Si scelga a caso un punto all’interno del cono. Si
determini la probabilità che tale punto risulti esterno alla sfera.
Soluzione
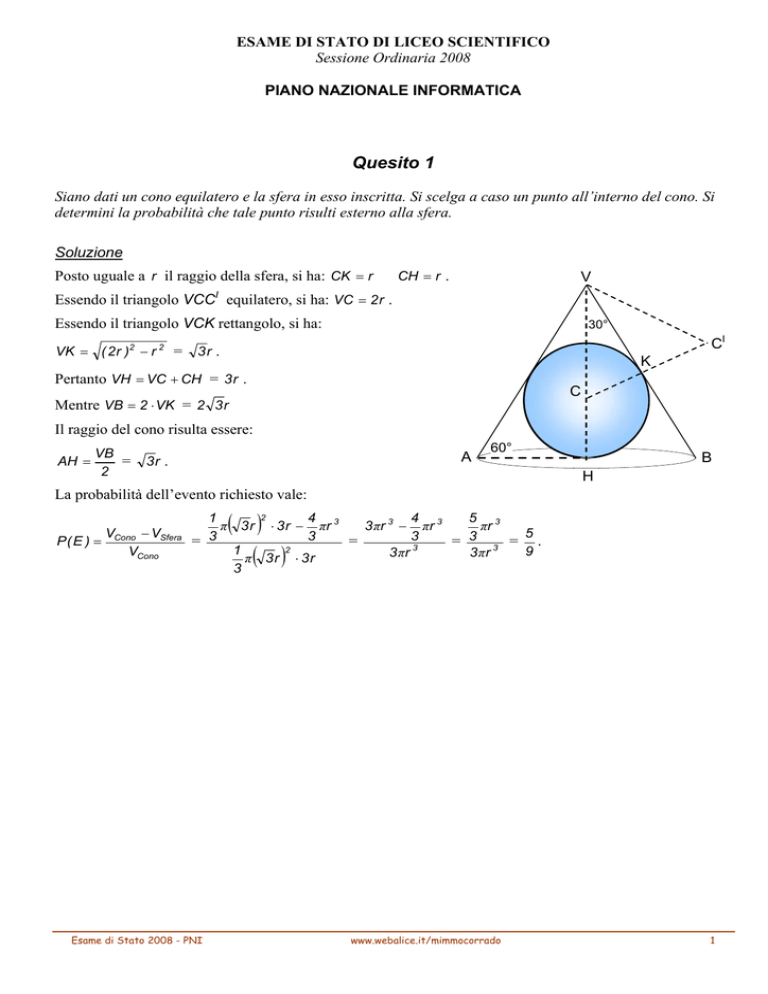
Posto uguale a r il raggio della sfera, si ha: CK = r
CH = r .
V
Essendo il triangolo VCCI equilatero, si ha: VC = 2 r .
Essendo il triangolo VCK rettangolo, si ha:
VK = ( 2 r )2 − r 2 =
30°
CI
3r .
K
Pertanto VH = VC + CH = 3 r .
C
Mentre VB = 2 ⋅ VK = 2 3 r
Il raggio del cono risulta essere:
AH =
VB
=
2
A
3r .
60°
B
H
La probabilità dell’evento richiesto vale:
( )
( )
2
4
5 3
1
4
πr
3 πr 3 − πr 3
π 3 r ⋅ 3 r − πr 3
VCono − VSfera
5
3
3
3
P( E ) =
= 3
=
=
= .
3
3
2
1
VCono
9
3 πr
3 πr
π 3r ⋅ 3r
3
Esame di Stato 2008 - PNI
www.webalice.it/mimmocorrado
1












