LE FUNZIONI SENO, COSENO E TANGENTE
1. LE FUNZIONI SENO E COSENO
DEFINIZIONE
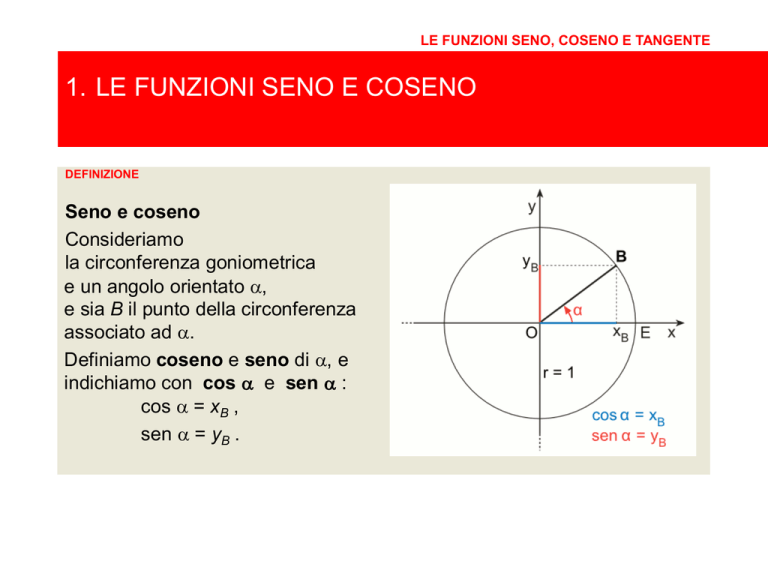
Seno e coseno
Consideriamo
la circonferenza goniometrica
e un angolo orientato α,
e sia B il punto della circonferenza
associato ad α.
Definiamo coseno e seno di α, e
indichiamo con cos α e sen α :
cos α = xB ,
sen α = yB .
LE FUNZIONI SENO, COSENO E TANGENTE
2. LE VARIAZIONI E IL GRAFICO DELLE FUNZIONI
SENO E COSENO
PROPRIETÀ
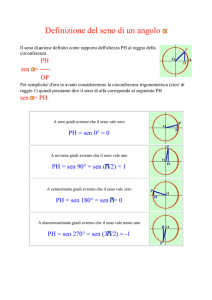
In particolare si verifica
che:
–1 ≤ sen x ≤ 1 ;
–1 ≤ cos x ≤ 1 ;
cos x = cos (–x) ;
sen x = –sen (–x) .
Costruiamo il grafico delle funzioni
y = sen x e y = cos x in [0; 2π]
riportando sull’asse x i valori degli
angoli e sull’asse y le coordinate
dei punti della circonferenza
goniometrica.
LE FUNZIONI SENO, COSENO E TANGENTE
4. LA PRIMA RELAZIONE FONDAMENTALE
Prima relazione fondamentale
della goniometria
cos2 α + sen2 α = 1
Da cui, se è noto cos α ,
,
mentre, se è noto sen α ,
.
LE FUNZIONI SENO, COSENO E TANGENTE
5. LA FUNZIONE TANGENTE
DEFINIZIONE
Tangente
Consideriamo un angolo orientato α,
e sia B il punto della circonferenza
associato ad α.
Definiamo tangente di α il rapporto,
quando esiste, tra l’ordinata e
l’ascissa di B:
.
LE FUNZIONI SENO, COSENO E TANGENTE
6. LE VARIAZIONI E IL GRAFICO DELLA FUNZIONE
TANGENTE
PROPRIETÀ
In particolare si verifica
che:
tg x tende a +∞ o –∞
quando x si avvicina a π/2,
tg x = – tg (–x).
Costruiamo il grafico della funzione y = tg x in [0;π]
riportando sull’asse x i valori degli angoli e sull’asse y
l’ordinata del punto T.
LE FUNZIONI SENO, COSENO E TANGENTE
8. LA SECONDA RELAZIONE FONDAMENTALE
Seconda relazione fondamentale della
goniometria
,
yB = sen α , xB = cos α ,
.