Test 06-02-17 - ex14-1-2011
Un cane ha partorito 10 cuccioli, tutti
di sesso femminile; considerando che
nella determinazione del sesso
p=q=0,5, quale era la probabilità che
tale evento si verificasse?
Nel caso di nascita di 10 cuccioli
quale è il numero di maschi e di
femmine che si osserva con maggiore
frequenza e quale è la sua probabilità?
10 punti
Leggendo un lavoro scientifico si trovano
pubblicati i seguenti dati:
DIETE
n
media
MSE o Varianza
dell'errore
1,3
a
B
6
2,8 b
C
6
3,2 c
1,133
Nota: medie con lettere differenti indicano differenze
significative per p<0,05; confronto fra le medie tramite
test t di Student.
note: means bearing different letters differ per p<0.05;
post hoc test: Student t test.
controlla se l’analisi statistica è stata fatta
correttamente ed eventualmente correggi le
lettere che che trovi errate. 10 punti
Alla schiusa rilevo il peso dei pulcini
dopo aver misurato il peso delle uova
prima della incubazione.
Rappresenta graficamente tali dati
calcolando l’equazione della retta di
regressione del peso del pulcino in
funzione del peso dell’uovo e la
10 punti
relativa significatività.
Combinazione
maschio femmina
10
0
9
1
8
2
7
3
6
4
5
5
4
6
3
7
2
8
1
9
0
10
TOTALE
A
6
ps*qr
n!/(s!*r!)
P%
0,00097656
0,00097656
0,00097656
0,00097656
0,00097656
0,00097656
0,00097656
0,00097656
0,00097656
0,00097656
0,00097656
1
10
45
120
210
252
210
120
45
10
1
0,0977%
0,9766%
4,3945%
11,7188%
20,5078%
24,6094%
20,5078%
11,7188%
4,3945%
0,9766%
0,0977%
100,0000%
1
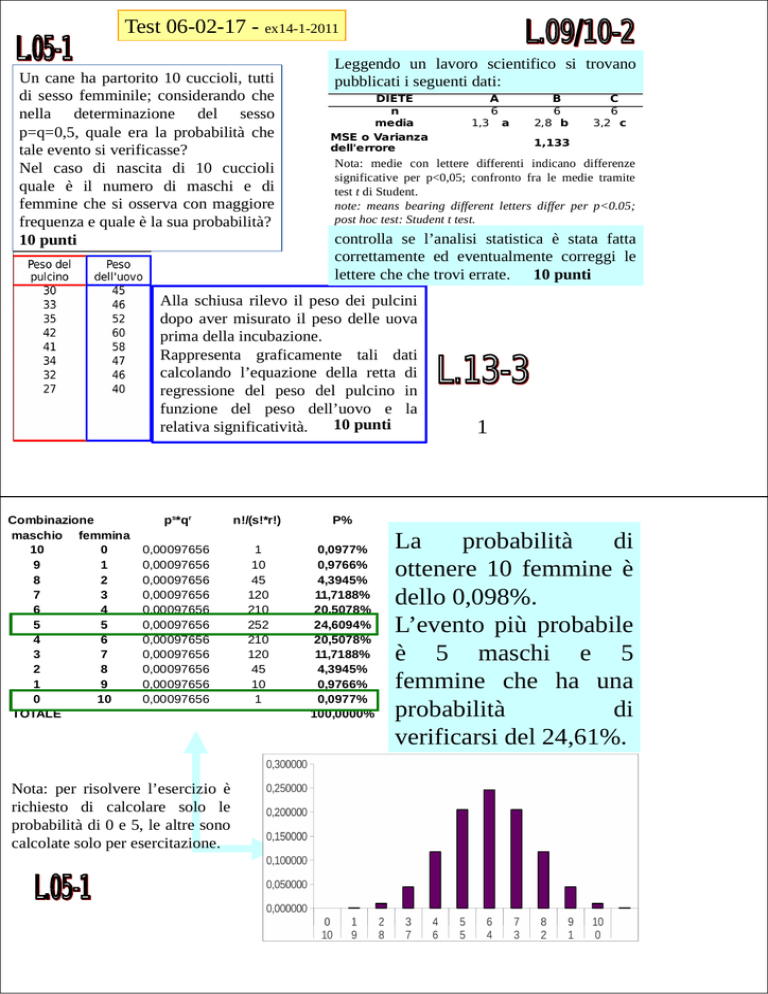
La
probabilità
di
ottenere 10 femmine è
dello 0,098%.
L’evento più probabile
è 5 maschi e 5
femmine che ha una
probabilità
di
verificarsi del 24,61%.
Nota: per risolvere l’esercizio è
richiesto di calcolare solo le
probabilità di 0 e 5, le altre sono
calcolate solo per esercitazione.
2
Analisi della varianza (non necessario)
DIETE
n
media
MSE o Varianza
dell'errore
dev.st.
A
6
1,3
a
C
6
3,2 c
1,133
0,52
SS errore=
SS trattamenti
B
6
2,8 b
1,133
1,33
x
1,17
17 =
19,26667
1,3 ^2 1,69 x 6
2,8 ^2 7,84 x 6
3,2 ^2
10 x 6
1,3 x
6 =
7,8
2,8 x
6 =
16,8
3,2 x
6 =
19,2
somma totale dei dati =
43,8
Termine di correzione
DIETE
trattamenti
errore
totale
SS
12,04
19,27
31,31
g.l.
2
15
17
=
=
=
10,14
47,04
61,44
118,620
^2
=
VAR
6,02
1,13
1918,44 :
18 = 106,580
12,040
F
5,3117647 > 3,682320344
< 6,358873481
Solo significativo
NB: Con l’analisi della varianza posso scoprire solo che ci sono delle differenze fra le medie senza sapere
fra quali. Devo fare il test delle minime differenze significative fra le coppie di medie preordinate per
sapere quali medie differiscono e quali no. Non è quindi necessario fare l’analisi della varianza perché
l’MS dell’errore che viene dall’analisi della varianza è già uno dei dati forniti. 3
n
media
MSE o Varianza
dell'errore
6
1,3 a
6
2,8 b
6
3,2 c
1,133
Calcolo la
4
Tavola realizzata con la funzione invt di libreoffice
probabilità % di un valore
due code
0,5
una coda
0,25
g.l.
1
1,000
2
0,816
3
0,765
4
0,741
5
0,727
6
0,718
7
0,711
8
0,706
9
0,703
10
0,700
11
0,697
12
0,695
13
0,694
14
0,692
15
0,691
16
0,690
17
0,689
18
0,688
19
0,688
20
0,687
21
0,686
22
0,686
23
0,685
24
0,685
25
0,684
26
0,684
27
0,684
28
0,683
29
0,683
30
0,683
40
0,681
60
0,679
80
0,678
100
0,677
1.000
0,675
infinito
0,674
più elevato di t trascurando il segno.
0,4
0,3
0,2
0,1
0,2
0,15
0,1
0,05
1,376
1,061
0,978
0,941
0,920
0,906
0,896
0,889
0,883
0,879
0,876
0,873
0,870
0,868
0,866
0,865
0,863
0,862
0,861
0,860
0,859
0,858
0,858
0,857
0,856
0,856
0,855
0,855
0,854
0,854
0,851
0,848
0,846
0,845
0,842
0,842
1,963
1,386
1,250
1,190
1,156
1,134
1,119
1,108
1,100
1,093
1,088
1,083
1,079
1,076
1,074
1,071
1,069
1,067
1,066
1,064
1,063
1,061
1,060
1,059
1,058
1,058
1,057
1,056
1,055
1,055
1,050
1,045
1,043
1,042
1,037
1,036
3,078
1,886
1,638
1,533
1,476
1,440
1,415
1,397
1,383
1,372
1,363
1,356
1,350
1,345
1,341
1,337
1,333
1,330
1,328
1,325
1,323
1,321
1,319
1,318
1,316
1,315
1,314
1,313
1,311
1,310
1,303
1,296
1,292
1,290
1,282
1,282
6,314
2,920
2,353
2,132
2,015
1,943
1,895
1,860
1,833
1,812
1,796
1,782
1,771
1,761
1,753
1,746
1,740
1,734
1,729
1,725
1,721
1,717
1,714
1,711
1,708
1,706
1,703
1,701
1,699
1,697
1,684
1,671
1,664
1,660
1,646
1,645
0,05
0,025
0,02
0,01
0,01
0,005
0,002
0,001
0,001
0,0005
12,710
4,303
3,182
2,776
2,571
2,447
2,365
2,306
2,262
2,228
2,201
2,179
2,160
2,145
2,131
2,120
2,110
2,101
2,093
2,086
2,080
2,074
2,069
2,064
2,060
2,056
2,052
2,048
2,045
2,042
2,021
2,000
1,990
1,984
1,962
1,960
31,820
6,965
4,541
3,747
3,365
3,143
2,998
2,896
2,821
2,764
2,718
2,681
2,650
2,624
2,602
2,583
2,567
2,552
2,539
2,528
2,518
2,508
2,500
2,492
2,485
2,479
2,473
2,467
2,462
2,457
2,423
2,390
2,374
2,364
2,330
2,326
63,660
9,925
5,841
4,604
4,032
3,707
3,499
3,355
3,250
3,169
3,106
3,055
3,012
2,977
2,947
2,921
2,898
2,878
2,861
2,845
2,831
2,819
2,807
2,797
2,787
2,779
2,771
2,763
2,756
2,750
2,704
2,660
2,639
2,626
2,581
2,576
318,310
22,327
10,215
7,173
5,893
5,208
4,785
4,501
4,297
4,144
4,025
3,930
3,852
3,787
3,733
3,686
3,646
3,610
3,579
3,552
3,527
3,505
3,485
3,467
3,450
3,435
3,421
3,408
3,396
3,385
3,307
3,232
3,195
3,174
3,098
3,090
636,620
31,599
12,924
8,610
6,869
5,959
5,408
5,041
4,781
4,587
4,437
4,318
4,221
4,140
4,073
4,015
3,965
3,922
3,883
3,850
3,819
3,792
3,768
3,745
3,725
3,707
3,690
3,674
3,659
3,646
3,551
3,460
3,416
3,390
3,300
3,291
5
1,37
2,228
Sempre uguale perché n uguale per tutte le tesi
metto in ordine crescente le medie:
1,3 vs. 2,8 = 1,5
1,3
2,8 vs. 3,2 = 0,4
2,8
3,2
6
La lettera sulla terza media era sbagliata
n
media
MSE o Varianza
dell'errore
6
1,3 a
6
2,8 b
6
3,2 b
1,133
Nota: medie con lettere differenti indicano differenze significative per
p<0,05; confronto fra le medie tramite test t di student.
note: means bearing different letters differ per p<0.05; post hoc test:
Student t test..
7
Il peso del pulcino è funzione del
peso dell’uovo!
l’equazione è:
Y = -1,847+0,7329x
;
8
Somme dei
quadrati degli
scarti
SS
Sorgenti di
variazione
gradi di
libertà
Varianze
Rapporti
gl o df
MS
F
deviazione dovuta
alla regressione 177,002276176
(SSxy)2/SSx2
1
177,002276176
163,4439514246
Deviazione dalla
regressione SSy 2(SSxy)2/SSx2
6,497723824
6
1,0829539707
Variazione
TOTALE di Y cioè
SSy2
183,50
g.l.
1
2
3
4
5
6
g.l.
1
2
3
4
5
6
7
1
161,4
18,51
10,13
7,709
6,608
5,987
1
4052
98,5
34,12
21,2
16,26
13,75
12,25
2
199,5
19
9,552
6,944
5,786
5,143
2
4999
99
30,82
18
13,27
10,92
9,547
L’equazione
trovata
è
altamente significativa (ha una
probabilità superiore allo 0,01
di essere la vera relazione
esistente fra peso uovo e peso
pulcino)
R2= 96,46%**
7
26,2142857143
0,9645900609
177,002/183,5
3
215,7
19,16
9,277
6,591
5,409
4,757
3
5404
99,16
29,46
16,69
12,06
9,78
8,451
4
224,6
19,25
9,117
6,388
5,192
4,534
4
5624
99,25
28,71
15,98
11,39
9,148
7,847
5
230,2
19,3
9,013
6,256
5,05
4,387
5
5764
99,3
28,24
15,52
10,97
8,746
7,46
6
234
19,33
8,941
6,163
4,95
4,284
6
5859
99,33
27,91
15,21
10,67
8,466
7,191
7
236,8
19,35
8,887
6,094
4,876
4,207
8
238,9
19,37
8,845
6,041
4,818
4,147
7
5928
99,36
27,67
14,98
10,46
8,26
6,993
9
240,5
19,39
8,812
5,999
4,772
4,099
8
5981
99,38
27,49
14,8
10,29
8,102
6,84
10
241,9
19,4
8,785
5,964
4,735
4,06
9
6022
99,39
27,34
14,66
10,16
7,976
6,719
12
243,9
19,41
8,745
5,912
4,678
4
10
6056
99,4
27,23
14,55
10,05
7,874
6,62
14
245,4
19,42
8,715
5,873
4,636
3,956
12
6107
99,42
27,05
14,37
9,888
7,718
6,469
16
246,5
19,43
8,692
5,844
4,604
3,922
14
6143
99,43
26,92
14,25
9,77
7,605
6,359
18
247,3
19,44
8,675
5,821
4,579
3,896
20
248
19,45
8,66
5,803
4,558
3,874
16
6170
99,44
26,83
14,15
9,68
7,519
6,275
18
6191
99,44
26,75
14,08
9,609
7,451
6,209
9
25
249,3
19,46
8,634
5,769
4,521
3,835
30
250,1
19,46
8,617
5,746
4,496
3,808
20
6209
99,45
26,69
14,02
9,553
7,396
6,155
40
251,1
19,47
8,594
5,717
4,464
3,774
25
6240
99,46
26,58
13,91
9,449
7,296
6,058
30
6260
99,47
26,5
13,84
9,379
7,229
5,992
Y = -1,847+0,7329x ; R2= 96,46%**
Sapendo che:
NOTA: b è un solo numero (g.l. di b=1) quindi poiché l’e.s. è pari alla d.s. diviso
la radice quadrata di 1, le due quantità sono uguali
Y =4,17+1,3161x; be.s.=0,0573 R2= 96,46%**
R2adj= 95,87%
10
va però disegnata solo la porzione di retta fra il valore
minimo e quello massimo delle x cioè fra 40 e 60 e non
oltre (non è lecito infatti ipotizzarne l'andamento oltre i
dati sperimentali osservati.
11












