La distribuzione campionaria di uno stimatore

La distribuzione campionaria
di uno stimatore
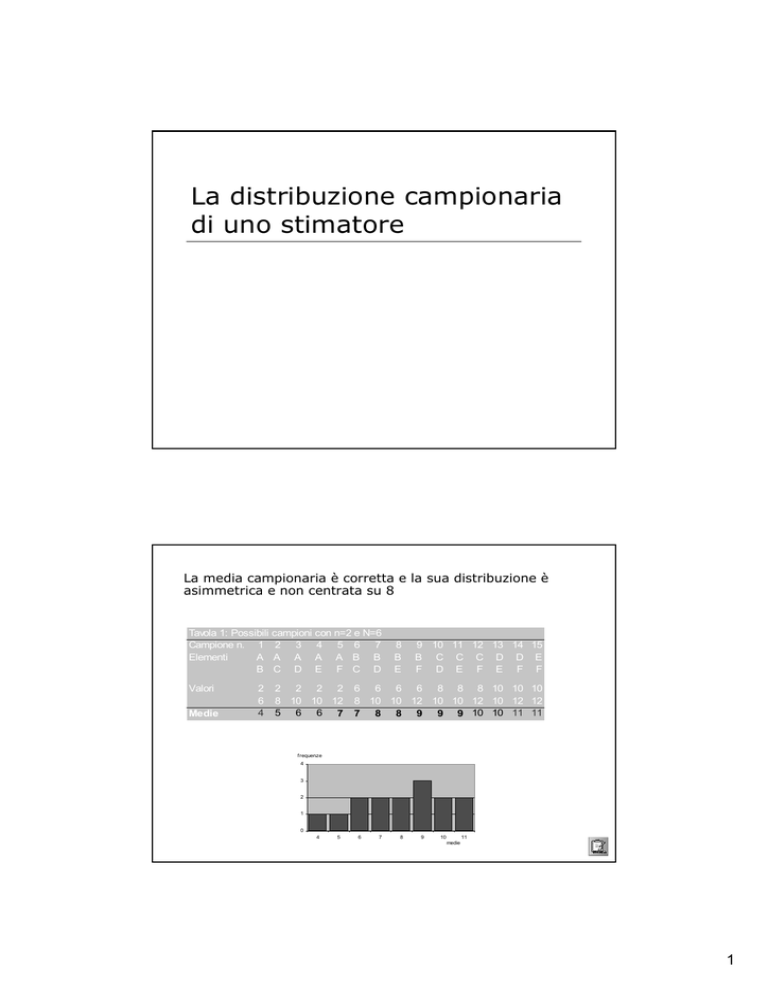
La media campionaria è corretta e la sua distribuzione è
asimmetrica e non centrata su 8
Tavola 1: Possibili campioni con n=2 e N=6
Campione n. 1 2 3 4 5 6 7
Elementi
A A A A A B B
B C D E F C D
Valori
Medie
2
6
4
2 2 2 2
8 10 10 12
5 6 6 7
8
B
E
9 10 11 12 13 14 15
B C C C D D E
F D E F E F F
6 6 6 6 8 8 8 10 10 10
8 10 10 12 10 10 12 10 12 12
7 8 8 9 9 9 10 10 11 11
frequenze
4
3
2
1
0
4
5
6
7
8
9
10
11
medie
1
Cambiamo stimatore: aggiungiamo 1 alla media quando esce 2 e
togliamo 1 alla media quando esce 12, perché sappiamo CE(2,12)
Tavola 1: Possibili
Campione n. 1
Elementi
A
B
Valori
campioni
2
3
A A
C D
2
6
5
Medie
frequenze
con n=2 e N=6
4
5 6
7
A A B B
E
F C D
2
2
2
2
8 10 10 12
6
7
7
7
8
B
E
9 10 11 12 13 14 15
B C C C D D E
F D E F E F F
6
6
6
6
8 8 8 10 10 10
8 10 10 12 10 10 12 10 12 12
7
8
8
8
9 9 9 10 10 10
Varianza=64/15
frequenze
4
5
3
4
Varianza=32/15
3
2
2
1
1
0
4
5
6
7
8
9
10
11
medie
0
4
5
6
7
8
9
10
11
medie
† Come la popolazione ha una sua deviazione standard,
quindi anche una sua varianza, in relazione al
carattere in oggetto (32/3), anche la popolazione di
tutte le medie campionarie ne ha una (64/15)
† Quale relazione esiste tra le due o varianze nel
CCSSR?
Var[ y ] =
64
15
Var[Y ] =
32
3
N −n 1
N −1 n
N −n 1
= SY2
N n
N −1
Var[Y ] = SY2
N
Var[ y ] = Var[Y ]
2
† Guardiamo bene al termine:
N −n 1 ⎛
n ⎞1
= ⎜1 − ⎟
N n ⎝ N⎠n
1
Situazione limite
1
n→N
n
1− → 0
N
n→N
2
1
→0
n
2
Situazione comune
n << N
n
f = →0
N
(1 − f ) → 1
1/n è il termine residuo che riduce la
varianza di popolazione per darci la
varianza delle medie campionarie
sulla variabilità delle stime, n ”pesa” in
termini assoluti non relativi!
3