esercizi Ultima Lezione (Prof.) con

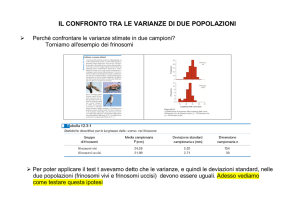
Esempi di individuazione dell’ipotesi H0 Esercizio 1 Ipotesi nulla e ipotesi alternativa: Esercizio 2 Ipotesi nulla e ipotesi alternativa: Regole per la scelta delle ipotesi Esercizio 3 Esercizio 4 Esercizio 5 Regione di Accettazione e Regione di Rifiuto Test a una coda e test a due code 1° caso – test a una coda 2° caso – test a una coda 3° caso – test a due code Test di ipotesi sulla media (varianza nota) Esercizio 1 Esercizio 2 Esercizio 3 Esercizio 4 Esercizio 5 Esercizio 6 Esercizio 7 Esercizio 8 Esercizio 9 Il p‐value Esercizio 10 Riprendiamo in esame i risultati ottenuti nell’esercizio 3. Test ipotesi sulla media (varianza incognita) Esercizio 1 Esercizio 2 Esercizio 3 Esercizio 4 Riassumiamo nella tabella 3 i vari procedimenti da seguire per effettuare un test di ipotesi sulla media µ di una popolazione. Test ipotesi sulla proporzione Esercizio 1 Esercizio 2 Esercizio 3 Esercizio 4 Esercizio 5 Test d’ipotesi sulla differenza tra due medie (varianze note) Dove d è una costante specificata, basandoci sulle medie di due campioni casuali indipendenti di ampiezza n1 ed n2. Ho l’ipotesi alternativa: Si usa la statistica Esercizio 1 Esercizio 2 Esercizio 3 Esercizio 4 Esercizio 5 Test d’ipotesi sulla differenza tra due medie (varianze incognite) Nel caso di grandi campioni le varianze incognite possono essere sostituite con i valori delle varianze campionarie dei due campioni. Se invece si usano piccoli campioni, per stimare la differenza tra le medie delle due popolazioni si può far ricorso alla distribuzione t, ma le due popolazioni devono avere distribuzione normale (e inoltre occorre distinguere due casi: quello in cui le varianze sono uguali e quelle in cui sono diverse). Nel caso in cui le due popolazioni normali hanno la stessa varianza, si ricava la stima congiunta della varianza comune con la seguente formula: Esercizio 1 Nella tabella sono riportate le lunghezze in cm di due campioni di oggetti dello stesso tipo prodotti da due macchine diverse. Esercizio 2 Esercizio 3 Test d’ipotesi sulla differenza tra due proporzioni Esercizio 1 Esercizio 2 Esercizio 3 Esercizio 4 Test di ipotesi sulla varianza e sullo scarto quadratico medio. Esercizio 1 Esercizio 2 Esercizio 3 Esercizio 4 Test di ipotesi sul rapporto di due varianze Se queste ipotesi sono verificate, si può affermare che la statistica: Questi valori possono essere letti sulla tavola della distribuzione F. Per tovare i valori critici si deve usare la formula: Esercizio 1 Esercizio 2 Esercizio 3 Esercizio 4 Esercizio 5 Esercizio 6