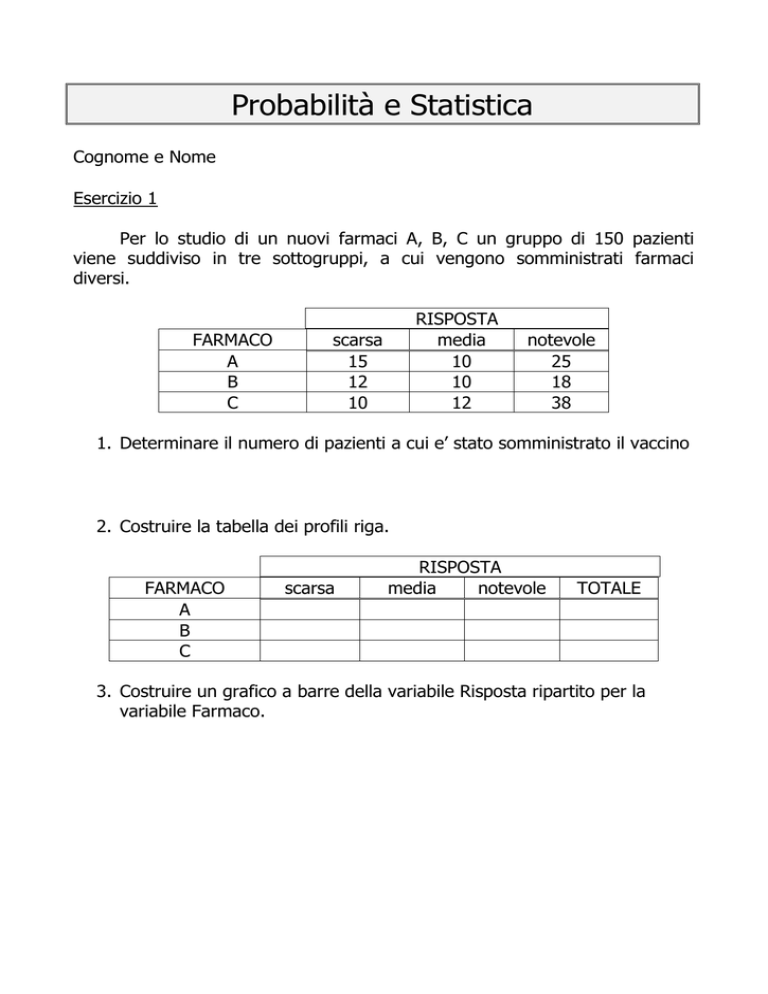
Probabilità e Statistica
Cognome e Nome
Esercizio 1
Per lo studio di un nuovi farmaci A, B, C un gruppo di 150 pazienti
viene suddiviso in tre sottogruppi, a cui vengono somministrati farmaci
diversi.
FARMACO
A
B
C
RISPOSTA
media
10
10
12
scarsa
15
12
10
notevole
25
18
38
1. Determinare il numero di pazienti a cui e’ stato somministrato il vaccino
2. Costruire la tabella dei profili riga.
FARMACO
A
B
C
scarsa
RISPOSTA
media
notevole
TOTALE
3. Costruire un grafico a barre della variabile Risposta ripartito per la
variabile Farmaco.
Esercizio 2
Due variabili X e Y sono rilevate sulla stessa popolazione di n=80
individui. Sono note le seguenti informazioni su X e Y :
la media della variabile X vale 1.2 m;
la media Y vale 8.3 kg;
2
la varianza di X vale 14.84m ;
2
la varianza Y vale 1.41Kg ;
corr(X,Y)=0.87;
1. Calcolare la retta di regressione e scriverne sotto l’espressione.
Commentare i risultati ottenuti.
2. Se cambiamo unita’ di misura a X e Y il coefficiente di correlazione cambia?
Perchè?
Esercizio 3
Nella seguente tabella è riportato il numero X di minuti di attesa
dell’autobus n. 17 rilevate alla stessa fermata in 12 giorni lavorativi e allo
stesso orario.
1
6
10
3
2
12
3
1
3
2
5
3
1. Calcolare il numero medio di minuti d’attesa e la varianza di X
X =
2X =
2. Disegnare il boxplot relativo alla variabile X
Esercizio 4
Un’industria alimentare che produce bibite dichiara che il contenuto
nominale di una lattina è 0.33 ml . In realtà il contenuto è una variabile
aleatoria di legge normale con media e varianza sconosciute.
Si scelgono n=20 lattine e si ottengono i seguenti risultati :
20
x i 6560 ,
i 1
20
(x i
i
328)2 194.56
1
a) Calcolare la media e la varianza campionaria.
H0 : =330
b) Effettuare un test a livello 5% con le seguenti ipotesi :
H1 : <330
c) Mantenendo le stesse ipotesi del punto b), se si accetta H0 a livello 5%,
a quale livello si è certi di accettare ancora l'ipotesi H0? (motivare ogni
affermazione)
10%
3%
Esercizio 5
Siano : X ~N(5,4) e Y=
X
5
2
Disegnare sugli stessi assi il grafico della legge di X e di Y.
Determinare il valore di a tale che P(X a)=0.484.
Calcolare P(Y -1)
Esercizio 6
Sia X una variabile aleatoria che assume i valori riportati in tabella con
legge f(X) :
x
-2
-1
0
2
f(x)
0.1
0.2
0
1. Completare la tabella e calcolare la media di X.
2. Determinare la probabilità che X sia minore o uguale a 0.
3. Determinare la probabilità che X sia compresa strettamente fra -1 e 2.
4. Determinare una legge g(X), tale che la media di X rispetto a questa legge
risulti maggiore di quella calcolata al punto 1. (giustificare la risposta)
x
g(x)
-2
-1
0
2
5. Costruire la funzione di ripartizione cumulata di g(x) , scriverne
l’espressione e disegnarne il grafico.
Esercizio 7
Nella tabella seguente sono riportati i valori di dieci campioni C1,C2,..,C10 di
numerosita' uguale a cinque estratti da una popolazione di varianza uguale a
2.
C1
27,2
-25,8
-9,7
24,8
16,0
C2
1,5
21,3
31,9
32,9
27,1
C3
2,0
0,6
-9,2
-11,9
8,5
C4
27,9
15,3
5,0
0,5
1,3
C5
13,9
30,3
7,4
8,0
-3,8
C6
31,6
0,5
7,9
7,9
31,5
C7
33,4
6,7
17,1
1,3
-5,1
C8
2,7
-5,8
22,9
-10,5
14,1
C9
8,2
4,0
2,0
14,3
-4,8
C10
11,8
39,0
-1,3
27,3
4,6
Scegliere uno dei campioni e riportare i dati nella tabella seguente.
x1
x2
x3
x4
x5
1. Utilizzando i dati scelti e riportati in tabella costruire un intervallo di
confidenza per la media a livello 95% .
Esercizio 8
Utilizzare i dati riportati in tabella per stabilire se la distribuzione della
variabile X ha legge uniforme (effettuare un test chi quadrato a livello 1%).
Variabile X
Valori osservati
Valori attesi
A
25
B
50
C
25












