5‐04‐2014
Abbiamo
introdotto alcuni indici statistici
(di posizione, di variabilità e di forma)
ottenibili da Excel con la funzione
Riepilogo Statistiche
Facciamo
qualche precisazione
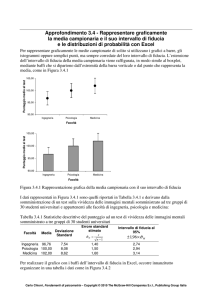
Al fine della partecipazione ad un concorso di
bellezza, alle 120 aspiranti miss viene chiesto il
colore dei capelli, ottenendo la tabella seguente
Colore dei capelli
Numero di aspiranti miss
Castano
50
Moro
45
Biondo
19
Rosso
6
Calcolare la moda e rappresentare graficamente
la distribuzione
1
5‐04‐2014
Si considera un carattere qualitativo di cui non
si dispongono delle osservazioni individuali
(ricordate l’esempio dei luoghi di vacanza?)
In questo caso, la moda è la modalità del
carattere con la più alta frequenza assoluta o,
equivalentemente, quello con la più alta
frequenza relativa (questo servirà per il grafico).
1)
2)
3)
4)
inserite i dati in una tabella
Calcolare le frequenze relative
Calcolare le percentuali (relative)
Per inserire il grafico (a torta),
selezionare i dati (colore/numero) e
inserirlo.
2
5‐04‐2014
Classe a cui corrisponde la massima densità di
frequenza (numero/ampiezza)
(se le classi sono tutte di uguale ampiezza è la
frequenza assoluta massima).
Esempio 2.2.2: In un collettivo di 100 ginnaste si
rileva il peso in kg. ottenendo la seguente tabella
Peso
45-48
48-50
50-55
55-60
Frequenza ass.
15
30
43
12
Occorre
calcolare l’ampiezza delle classi
La densità si ottiene dividendo la
frequenza sull’ampiezza dell’intervallo
Si
otterrà che il valore più alto
corrisponde alla classe 48-50 (classe
modale).
3
5‐04‐2014
In
Excel la funzione MEDIANA si può
usare solo per caratteri quantitativi,
avendo a disposizione le osservazioni
individuali.
Cosa succede se abbiamo delle
distribuzioni di frequenza? L’ordinamento
delle unità viene effettuato attraverso le
frequenze cumulate
La
seguente tabella mostra la
distribuzione di 100 donne in relazione al
numero di figli
Calcolare
N.Figli
N.donne
0
14
1
45
2
28
3
8
4
5
la mediana
4
5‐04‐2014
Le
classi sono già ordinate dal valore più
basso a quello più alto.
Per individuare le unità centrali, occorre
calcolare le frequenze cumulate
Siccome ci sono 100 unità, occorre
individuare la 50° e la 51° e vedere in
quale classe ricadono (sarà la seconda).
5
5‐04‐2014
L’analisi statistica spesso studia i fenomeni
collettivi confrontandoli con modelli teorici
di riferimento.
Tra di essi, vedremo: la distribuzione binomiale,
la distribuzione di Poisson, la distribuzione
normale o Gaussiana, e altre.
Scopo:
Molti fenomeni sono approssimabili con esse
Inferenza statistica: dai dati di un campione
verificare ipotesi sull’intera popolazione
Variabile aleatoria (o casuale): quantità il cui
valore dipende dal risultato di un
esperimento (ad es., “numero delle volte in
cui esce testa”).
V.a. discrete = assume valori
in un insieme numerabile
(ad es., lancio del dado,
estrazione di una pallina da
un’urna)
V.a. continue= assume
un’infinità non numerabile di
valori (intervallo reale), ad
es. durata (peso, diametro…)
di un pezzo meccanico…
6
5‐04‐2014
Quando
si fanno corrispondere ai valori
che X può assumere i rispettivi livelli di
probabilità, si ha la distribuzione di
probabilità
Funzione di (massa o di) probabilità: il
legame di dipendenza tra i valori che la
variabile X può assumere (P(X=x)=1/2…)
Funzione di ripartizione: associa ad ogni
valore x la probabilità che X assuma
valori ≤ x.
Uniforme
discreta (estrazione casuale di
una pallina tra 1 e N, esiti di un lancio del
dado)
Bernoulli (esperimento con due esiti
disgiunti)
Binomiale (serie di prove di Bernoulli
indipendenti con la stessa probabilità di
successo
7
5‐04‐2014
E’ la distribuzione di probabilità usata quando:
le prove ripetute sono indipendenti
i risultati di ciascuna prova sono due
la probabilità p di successo è costante
Esempi: un sondaggio in cui ogni persona può
esprimere SI o NO; un test di qualità sul
funzionamento di un elettrodomestico
(funziona, non funziona)
Per calcolare la densità di probabilità (ossia la probabilità che una
variabile assuma un certo valore) di una distribuzione binomiale, in
Excel si usa la funzione
DISTRIB.BINOM(num_successi;prove;probabilità_s;cumulativo)
oppure
DISTRIB.BINOM.N(num_successi;prove;probabilità_s;cumulativo)
Dove
◦ Num_successi = numero di successi in prove (x nella formula)
◦ Prove= numero di prove indipendenti (n nella formula)
◦ Probabilità_s= probabilità di successo per ciascuna prova (p nella formula)
◦ Cumulativo= valore logico che determina la forma assunta dalla funzione.
Se è VERO, DISTRIB.BINOM restituirà la funzione distribuzione cumulativa, ovvero la
probabilità che venga restituito un numero di successi ≤ di num_successi:
Se è FALSO, verrà restituita la funzione massa di probabilità, ovvero la probabilità che venga
restituito un numero massimo di successi = al valore di num_successi ,che è
corrispondente alla densità di probabilità
8
5‐04‐2014
◦ La distribuzione binomiale permette di calcolare,
per numeri n piccoli, le probabilità di avere un
certo numero k di successi nelle n prove.
◦ Se abbiamo molte prove, n diventa molto grande
e trovare le probabilità dei successi k diventa
difficile.
◦ Per valori alti di n il problema non è di trovare
la probabilità connessa ad uno specifico numero
k di successi, ma di trovare ad esempio la
probabilità di trovare più o meno di k
successi.
Si usa quando la probabilità di successo p è piccola, il numero
n delle prove è molto elevato e il prodotto λ=np è finito.
La funzione di probabilità della distribuzione di Poisson è:
In Excel POISSON(x; media; cumulativo) dove
Media = λ
cumulativo = valore logico. Se è VERO, restituisce la
funzione di distribuzione cumulativa P(X≤x); se è FALSO
P(X=x)
Provate con i dati dell’Esempio 7.5 e 7.6, p. 165 [B]
9
5‐04‐2014
A
partire dall’insieme dei valori reali che
X può assumere, la funzione densità di
probabilità descrive come la variabile di
distribuisce rispetto al supporto
Modelli probabilistici nel continuo: uniforme,
normale (o gaussiana)
◦ Si ricorre alle distribuzioni NORMALE
(GAUSSIANA), o di Poisson, che valgono per n
molto grande.
◦ In questo caso lo scaloide della distribuzione di
probabilità binomiale, ossia l’insieme dei rettangoli
che rappresentano le probabilità dei singoli k,
tende a diventare un’area sottostante ad una linea
continua.
10
5‐04‐2014
Per il calcolo della funzione di probabilità normale, in Excel si
usa
DISTRIB.NORM.N(x0;media;dev_standard;cumulativo)
Dove:
x0 = valore per il quale si desidera la distribuzione
media=media aritmetica della distribuzione (µ nella formula)
dev_standard=deviazione standard della distribuzione (σ nella formula)
Cumulativo=valore logico. Se è VERO, restituisce la funzione di
distribuzione cumulativa
se è FALSO, restituisce la funzione massa di probabilità P(X= x0)
(altezza della curva a campana della densità di probabilità)
Distribuzione
χ2
Distribuzione t di Student
Distribuzione F di Fisher (per la
regressione)
11
5‐04‐2014
E’ una distribuzione di probabilità continua, ottenuta come
somma dei quadrati di n variabili casuali indipendenti, con
media 0 e varianza 1
Caratteristiche:
◦ L’asimmetria
◦ La dipendenza dal parametro n
◦ La non negatività della funzione
◦ Al variare di n esistono infinite distribuzioni
In Excel si usa la funzione
DISTRIB.CHI(x;gradi_libertà)
gdl=n
E’ una distribuzione di probabilità continua.
Consideriamo due variabili indipendenti Z, Q, dove
◦ Z è distribuita normalmente con media 0 e varianza 1
◦ Q è distribuita secondo un χ2 con n gradi di libertà
Si può dimostrare che la variabile casuale continua
segue una distribuzione t di Student con n gradi di libertà
12
5‐04‐2014
Caratteristiche:
◦ Simmetrica rispetto al valor
medio
◦ Dipende da n
◦ All’aumentare di n tende alla
distribuzione normale
◦ Per ogni valore di n si ha una
diversa distribuzione
In Excel si usa la funzione
DISTRIB.T(x;gradi_libertà;coda)
Se coda=1 (risp. 2), viene restituita una
distribuzione a 1 coda (risp. 2 code).
E’ una distribuzione usata per confrontare il grado di
variabilità di due insiemi di dati ed è usata nello studio
dell’analisi della varianza (ANOVA)
Consideriamo due variabili casuali X1 e X2
◦ distribuite secondo un χ2 con n1 e n2 gradi di libertà, risp.
Si può dimostrare che la variabile
F= (X1/n1) / (X2/n2)
segue una distribuzione F con n1 e n2 gradi di libertà
13
5‐04‐2014
In Excel si usa la funzione
DISTRIB.F(x;gradi_libertà1; gradi_libertà2)
Inferenza statistica
Indagine campionaria: indagine svolta su una parte
dell’intero collettivo da indagare (popolazione)
Estendere i risultati a tutta la popolazione: i risultati
ottenuti per il campione sono approssimativamente
validi per tutta la popolazione
14
5‐04‐2014
In una officina sono installate 5 macchine uguali.
Ciascuna ha la probabilità del 20% di guastarsi.
Studiare la variabile X=n° di macchine guaste
contemporaneamente
DISTRIB.BINOM.N(num_successi;prove;probabilità_s;cumulativo)
Risulta che:
Num_successi= da 0 a 5
Prove= 5
Probabilità_s=0,2
Cumulativo=falso
1
2
3
A
n=
p=
q=
B
5
0,2
0,8
In una officina sono installate 5 macchine uguali.
Ciascuna ha la probabilità del 20% di guastarsi.
Studiare la variabile X=n° di macchine guaste
contemporaneamente
(Usare il trascinamento)
4
5
X
P(X)
6
0
0,32768
7
1
0,40960
8
2
0,20480
9
3
0,05120
10
4
0,00640
11
5
0,00032
=DISTRIB.BINOM(A6;$B$1;$B
$2;FALSO)
Inserire anche un istogramma della
densità di probabilità (selezionando
come ascissa la colonna X)
15
5‐04‐2014
Densità di probabilità per il numero di macchine guaste
0,45
0,40
0,35
0,30
0,25
0,20
0,15
0,10
0,05
0,00
0
1
2
3
4
5
In una ditta lavorano 12 operai che usano apparecchiature
collegate alla stessa rete elettrica. Ogni operaio dispone
di un’apparecchiatura che assorbe 1 kilowatt e la usa, in
modo indipendente dagli altri, per 10 minuti ogni ora.
Se la potenza della rete è di 5 kilowatt, qual è la
probabilità che non ci sia sovraccarico?
p= 1/6 =1,1666=0,2 (probabilità che un operaio usi un’apparecchiatura)
n=12
X=5 (la rete non è in sovraccarico se 5 o meno operai usano le loro
apparecchiature). Num_successi=X
Cumulativo=vero
A
B
1 n= 12
2 p= 0,2
=DISTRIB.BINOM(5;$B$1;$B$2;VERO)
3 q= 0,8
0,99207496
16
5‐04‐2014
Determinare la distribuzione di probabilità del numero X
di pezzi difettosi, se si sono provati 20 pezzi di un lotto,
dove normalmente quelli difettosi sono il 10%.
Rappresentare graficamente la distribuzione ottenuta
Dal problema risulta che
N=20
P=10/100=0,1
Occorre calcolare P(X) con 0<=X<=20
(cumulativo=falso) Formattare le celle relative a P(X) come numero
1
2
3
X
P(X)
0
0,1215767
1
0,2701703
2
0,2851798
3
0,1901199
4
0,0897788
5
0,0319214
6
0,0088670
7
0,0019705
8
0,0003558
9
0,0000527
10
0,0000064
11
0,0000007
12
0,0000001
13
0,0000000
14
0,0000000
15
0,0000000
16
0,0000000
17
0,0000000
18
0,0000000
19
0,0000000
20
0,0000000
A
n=
p=
q=
B
20
0,1
0,9
=DISTRIB.BINOM(A6;$B$1;$B$2;FALSO)
0
17
5‐04‐2014
Determinare la distribuzione di probabilità del numero X
di pezzi difettosi, se si sono provati 20 pezzi di un lotto,
dove normalmente quelli difettosi sono il 10%.
Rappresentare graficamente la distribuzione ottenuta.
Determinare
◦ Il numero medio di pezzi difettosi (=20*0,1)
◦ La probabilità che meno di 7 pezzi siano difettosi
P(X≤6)=
=DISTRIB.BINOM(6;$B$1;$B$2;VERO)
0,997613911
Num_successi
18