Approfondimento 3.4 - Rappresentare graficamente
la media campionaria e il suo intervallo di fiducia
e le distribuzioni di probabilità con Excel
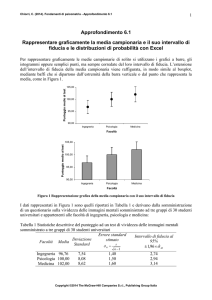
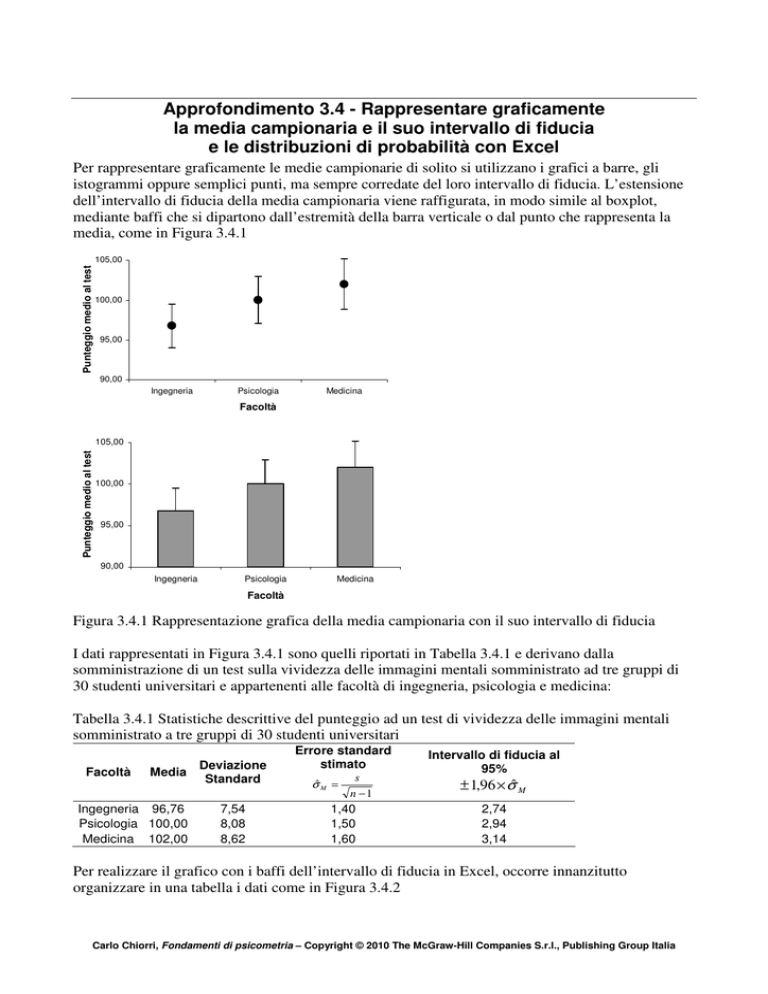
Per rappresentare graficamente le medie campionarie di solito si utilizzano i grafici a barre, gli
istogrammi oppure semplici punti, ma sempre corredate del loro intervallo di fiducia. L’estensione
dell’intervallo di fiducia della media campionaria viene raffigurata, in modo simile al boxplot,
mediante baffi che si dipartono dall’estremità della barra verticale o dal punto che rappresenta la
media, come in Figura 3.4.1
Punteggio medio al test
105,00
100,00
95,00
90,00
Ingegneria
Psicologia
Medicina
Facoltà
Punteggio medio al test
105,00
100,00
95,00
90,00
Ingegneria
Psicologia
Medicina
Facoltà
Figura 3.4.1 Rappresentazione grafica della media campionaria con il suo intervallo di fiducia
I dati rappresentati in Figura 3.4.1 sono quelli riportati in Tabella 3.4.1 e derivano dalla
somministrazione di un test sulla vividezza delle immagini mentali somministrato ad tre gruppi di
30 studenti universitari e appartenenti alle facoltà di ingegneria, psicologia e medicina:
Tabella 3.4.1 Statistiche descrittive del punteggio ad un test di vividezza delle immagini mentali
somministrato a tre gruppi di 30 studenti universitari
Facoltà
Deviazione
Media
Standard
Ingegneria 96,76
Psicologia 100,00
Medicina 102,00
7,54
8,08
8,62
Errore standard
stimato
σˆ M =
s
n −1
1,40
1,50
1,60
Intervallo di fiducia al
95%
± 1,96 × σˆ M
2,74
2,94
3,14
Per realizzare il grafico con i baffi dell’intervallo di fiducia in Excel, occorre innanzitutto
organizzare in una tabella i dati come in Figura 3.4.2
Carlo Chiorri, Fondamenti di psicometria – Copyright © 2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Figura 3.4.2 Organizzazione nel foglio di Excel dei dati da rappresentare graficamente
Si crea poi il grafico selezionando le celle riguardanti l’etichetta della categoria (colonna Facoltà) e
la media corrispondente (colonna M) e clickando sull’icona che permette di creare un grafico
(oppure dal menu a tendina Inserisci → Grafico). Possiamo scegliere se creare un grafico a barre
(Istogramma) oppure a punti (Linee). Nel caso del grafico a barre, dopo averlo creato si selezionano
le barre, si fa doppio click col tasto sinistro del mouse e si sceglie dalla finestra Formato serie dati
la linguetta Barre di errore Y. In questo menu possiamo scegliere se vogliamo un baffo oppure due,
ma soprattutto possiamo inserire nel campo Personalizza l’estensione dell’intervallo di fiducia
di Personalizza +, è possibile
± 1,96 × σˆ M per tutte e tre le medie. Clickando sul pulsantino
andare a selezionare col mouse la colonna che contiene le estensioni degli intervalli di fiducia, come
in Figura 3.4.3:
Figura 3.4.3 Selezione dell’intervallo di celle che contiene le estensioni degli intervalli di fiducia
della media campionaria
Clickando su
si torna alla finestra della funzione e si ripete l’operazione per Personalizza −. A
quel punto si clicka su OK e il gioco è fatto.
Nel caso del grafico a punti, occorre creare un grafico a linee, eliminare le linee e lasciare
solo i punti. Per fare questo, una volta creato il grafico, basta clickare due volte col tasto sinistro del
mouse sulla linea o sui punti e nella linguetta Motivo, riquadro Linea, spuntare Assente. Per inserire
i baffi, basta poi andare sulla linguetta Barre di errore Y e procedere come nel caso delle barre.
Excel permette di calcolare anche l’estensione dell’intervallo di fiducia mediante la funzione
=CONFIDENZA(alfa;dev_standard;dimensioni) dove alfa è il livello di probabilità dell’intervallo
di fiducia, dev_standard è la deviazione standard della popolazione, e dimensioni è l’ampiezza
campionaria.
Excel permette anche di ottenere il punto z corrispondente ad una certa probabilità e la
probabilità associata ad un certo punto z. Nel primo caso, utilizzando la funzione
=DISTRIB.NORM.ST(z) viene restituita l’area della curva normale inferiore a quel particolare z.
Questo significa che se inserite z = 1,96 ottenete come risultato ,975. Nel secondo caso si utilizza la
formula inversa =INV.NORM.ST(probabilità), per cui viene restituito il punto z relativo ad un
certo valore di area che va da −infinito alla probabilità che avete inserito. Se inserite quindi il valore
di probabilità ,05, ottenete come risultato −1,645.
La distribuzione binomiale è invece ottenibile mediante la funzione
=DISTRIB.BINOM(num_successi;prove;probabilità_s;cumulativo), dove num_successi è il numero
di successi k, prove il numero di prove n, probabilità_s è la probabilità del successo e cumulativo vi
permette di avere la probabilità cumulata (ossia la probabilità di ottenere da zero a k successi) se
Carlo Chiorri, Fondamenti di psicometria – Copyright © 2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia
scrivete VERO oppure quella di massa (ossia la probabilità di ottenere esattamente k successi) se
scrivete FALSO. Quindi la funzione =DISTRIB.BINOM(5;10;0,50;VERO) restituisce il valore ,62,
ossia la probabilità di ottenere un numero di successi minore o uguale a 5 su 10 prove con
p(successo) = ,50, mentre la funzione =DISTRIB.BINOM(5;10;,50;FALSO) restituisce il valore
,246, ossia la probabilità di ottenere esattamente 5 successi su 10 prove.
Carlo Chiorri, Fondamenti di psicometria – Copyright © 2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia