Derivazione della legge della giunzione

Dispositivi e Circuiti Elettronici
1
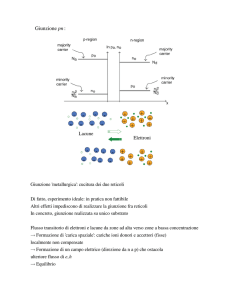
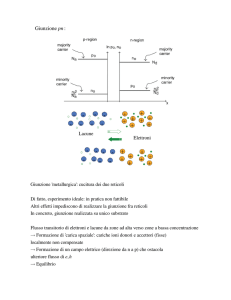
Derivazione della legge della giunzione
La dimostrazione della legge della giunzione può essere condotta secondo
quanto segue. In condizioni di equilibrio termodinamico, si ha
n2i
np0 (−xp ) =
NA
n2i
pn0 (xn ) =
ND
nn0 (xn ) = ND ,
pp0 (−xp ) = NA ,
(1)
(2)
Tenendo conto della (1), l’espressione del potenziale di contatto ricavata
dal diagramma abande come differenza dei lavori di estrazione nel due lati
neutri ammette l’interpretazione:
Vbi = VT log
NA ND
nn0 (xn )
=
V
log
T
np0 (−xp )
n2i
(3)
Analogamente, a partire dalla (2) la stessa relazione ammette l’intepretazione:
pp0 (−xp )
NA ND
= VT log
(4)
Vbi = VT log
2
pn0 (xn )
ni
Invertendo (3) e (4) si ottiene:
µ
¶
µ
¶
pn0 (xn )
Vbi
np0 (−xp )
Vbi
= exp −
,
= exp −
(5)
pp0 (−xp )
VT
nn0 (xn )
VT
Fuori dall’equilibrio termodinamico, la caduta di potenziale sulla regione
svuotata passa da Vbi a Vbi −V . In basso livello di iniezione, si può assumere
che la (5) continui a valere, modificata tenendo conto della variazione di
caduta di potenziale sulla regione di svuotamento
µ
¶
µ
¶
Vbi − V
np (−xp )
Vbi − V
pn (xn )
≈ exp −
,
≈ exp −
pp (−xp )
VT
nn (xn )
VT
(6)
Sempre per l’ipotesi di basso livello di iniezione, anche fuori equilibrio
i portatori maggioritari possono essere assunti in concentrazione pari al
valore di equilibrio, ovvero:
nn (xn ) ≈ nn0 (xn ) = ND ,
Lezione U2-L2, Slide 49
pp (−xp ) ≈ pp0 (−xp ) = NA
(7)
c 2005 Politecnico di Torino
°
Dispositivi e Circuiti Elettronici
2
Sostituendo (7) nella (6), si ricava
¶
µ ¶
µ
V
Vbi
exp
,
pn (xn ) = NA exp −
VT
VT
µ
¶
µ ¶
Vbi
V
np (−xp ) = ND exp −
exp
VT
VT
che, grazie a (1), (2) e (5), conduce alla legge della giunzione
µ ¶
µ ¶
V
V
pn (xn ) = pn0 (xn ) exp
,
np (−xp ) = np0 (−xp ) exp
VT
VT
(8)
(9)
Infine, ricordando che l’eccesso di carica è definito come la differenza tra
il valore della concentrazione di carica ed il valore in equilibrio, la (8) viene
spesso espressa nella forma:
·
µ ¶
¸
V
0
pn (xn ) = pn0 (xn ) exp
−1 ,
VT
(10)
·
µ ¶
¸
V
n0p (−xp ) = np0 (−xp ) exp
−1
VT
Lezione U2-L2, Slide 49
c 2005 Politecnico di Torino
°
Dispositivi e Circuiti Elettronici
Calcolo delle densità di corrente nella
regione svuotata in assenza di GR
L’ipotesi di assenza di fenomeni di GR nella regione di svuotamento si
esprime matematicamente secondo:
Un (x) = Up (x) = 0
per −xp < x < xn
(1)
Le equazioni di continuità di elettroni e lacune in condizioni stazionarie nel
tempo, quindi, assumono la forma
dJn
= qUn = 0,
dx
dJp
= −qUp = 0
dx
(2)
ovvero, le densità di corrente di elettroni e lacune sono costanti nella regione
di svuotamento. Di conseguenza, si ha
Jp (−xp ) = Jp (xn ) ≈ Jp,diff (xn ),
Jn (xn ) = Jn (−xp ) ≈ Jn,diff (−xp ) (3)
dove il segno di approssimazione dipende dal fatto che nella regione quasineutra il campo elettrico è molto piccolo, almeno se la corrente totale
non è troppo elevata, consentendo quindi di trascurare la componente di
trascinamento dei portatori minoritari rispetto a quella di diffusione.
Lezione U2-L2, Slide 57
c 2005 Politecnico di Torino
°