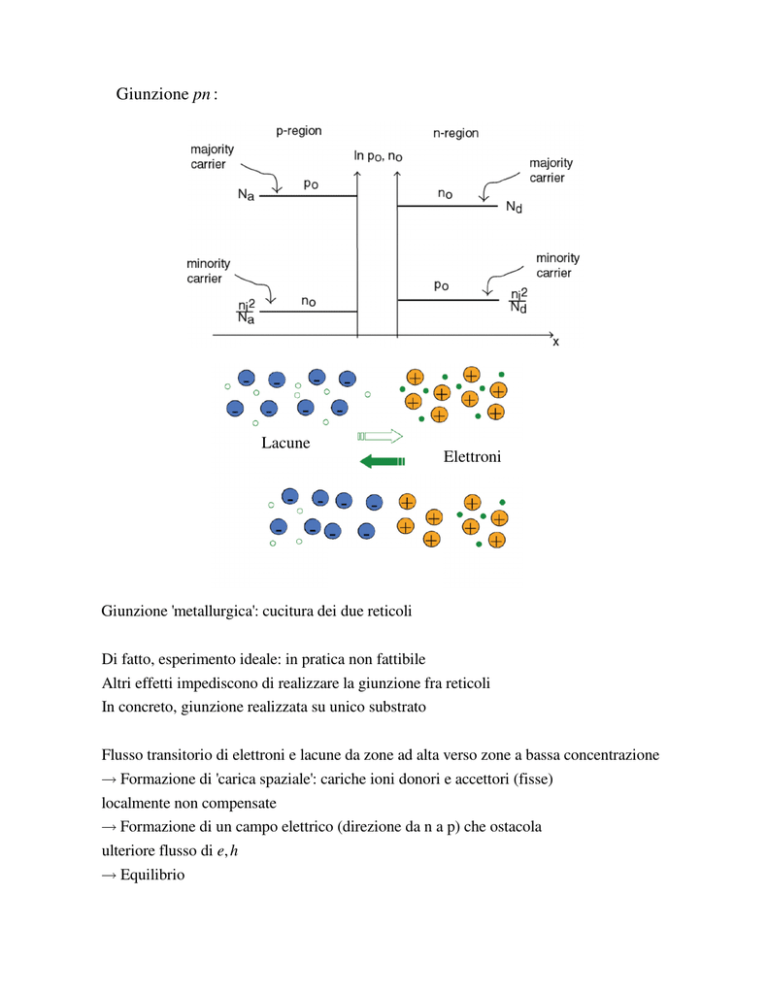
Giunzione pn :
Lacune
Elettroni
Giunzione 'metallurgica': cucitura dei due reticoli
Di fatto, esperimento ideale: in pratica non fattibile
Altri effetti impediscono di realizzare la giunzione fra reticoli
In concreto, giunzione realizzata su unico substrato
Flusso transitorio di elettroni e lacune da zone ad alta verso zone a bassa concentrazione
→ Formazione di 'carica spaziale': cariche ioni donori e accettori (fisse)
localmente non compensate
→ Formazione di un campo elettrico (direzione da n a p) che ostacola
ulteriore flusso di e, h
→ Equilibrio
Formazione dello strato di svuotamento:
Concentrazioni:
Approssimazione di svuotamento:
Approx. di svuotamento
x < −x p 0 :
ni2
p0 ( x) = N A , n0 ( x) =
NA
−x p 0 < x < 0 :
p0 ( x) , n0 ( x) ≪ N A
0 < x < + xn 0 :
n0 ( x) , p0 ( x) ≪ N D
x > + xn 0 :
n0 ( x) = N D , p0 ( x ) =
ni2
ND
Densita’ di carica elettrica:
Approx. di svuotamento
Esatta
x < −x p 0 :
ρ ( x) = 0
−x p 0 < x < 0 :
ρ ( x) = −qN A
0 < x < + xn 0 :
ρ ( x) = qN D
x > + xn 0 :
ρ ( x) = 0
Campo elettrico: Eq. di Poisson
∇⋅ E =
ρ
ρ
dE
→
= ,
ε0
dx ε0
1D
x2
1
E ( x2 ) − E ( x1 ) = ∫ ρ ( x ) dx
ε x
1
x < −x p 0 :
E ( x) = 0
−x p 0 < x < 0 :
E ( x ) − E (−x p 0 ) = −
0 < x < + xn 0 :
E ( x) =
x > + xn 0 :
E ( x) = 0
qN A x
qN
x −x = − A ( x + x p 0 )
p0
εs
εs
qN D
( x − xn 0 )
εs
Potenziale elettrostatico:
x
V ( x) = −∫ E ( x ') dx '
x0
E ( x) = 0
x < −x p 0 :
→ V ( x) = V0 = V (−x p 0 ) ≡ 0
−x p 0 < x < 0 :
E ( x) = −
qN A
( x + xp0 )
εs
qN
2
2
2
qN A
qN A
→ V ( x) = − ∫ − A ( x '+ x p 0 )dx ' =
x + x p 0 ) − (−x p 0 + x p 0 ) =
x + xp0 )
(
(
εs
2εs
2εs
−xp0
x
→ V (0) =
qN A 2
xp0
2εs
0 < x < + xn 0 :
E ( x) =
qN D
( x − xn 0 )
εs
qN
qN
qN
2 x
→ V ( x) = −∫ D ( x '− xn 0 )dx ' = − D ( x − xn 0 ) = − D
εs
0
2εs
2εs
0
q
2
→ V ( x) =
−N D ( x − xn 0 ) + N D xn20
2εs
x
2
2
( x − xn 0 ) − (0 − xn 0 )
xn 0 2
q
→ V (0) = 0, V ( xn 0 ) = N D
εs
2
Richiedendo V ( x) continuo in x = 0, occorre aggiungere la costante
possibile perche' soluzioni in segmenti diversi sono indipendenti
qN A 2
q
→ V (0) =
x p 0 → V ( xn 0 ) =
N D xn 0 2 + N A x 2p 0 )
(
2εs
2εs
x > + xn 0 :
E ( x) = 0
→ V ( x) = V ( xn 0 ) = V ( xn 0 ) −V (−x p 0 ) =
=0 (conv)
q
N A x 2p 0 + N D xn20 ≡ Vbi
2εs
qN A 2
xp0 :
2εs
Per determinare la zona di svuotamento:
1) Neutralita' globale
qN A x p 0 = qN D xn 0
carica totale lato n
carica totale lato p
2) Potenziale di built-in
µn dV 1 dn
=
Dn dx n dx
q dV 1 dn d (ln n)
=
=
Relazione di Einstein
kT dx n dx
dx
q
n
→
(V −V0 ) = ln
kT
n0
→ n = n0 e
q(V −V0 )
kT
Fissando n = ni per V = 0 :
−
ni = n0 e
qV0
kT
→ n = ni e
qV
kT
→ p = pi e
−
V = 0
→ OK con 0
n0 = ni
≈ ND
qV
kT
≈ NA
kT N D
Vn =
ln
q
ni
→
kT N
V p = − ln A
q
ni
kT N D
N A kT N D N A
=
→ Vbi = Vn −V p ≈
+
ln
ln
ln
Tensione di built-in
q ni
ni q
ni2
qN A x p 0 = qN D xn 0
Vbi =
kT N D N A
q
=
ln
2
q
ni
2εs
N A x 2p 0 + N D xn20
Larghezza dello strato di svuotamento:
2εsVbi N A
xn 0 =
q ( N A + N D ) N D
2εsVbi N D
xp0 =
q ( N A + N D ) N A
→ xn 0 + x p 0 =
2εsVbi ( N A + N D )
qN D N A
Trovato il modo di generare f.e.m/corrente elettrica gratis?
Stiamo violando un paio di principi della termodinamica?
Giunzioni metallo-semiconduttore per contatti alle estremita':
non si puo' misurare Vbi
non passa corrente in un circuito esterno
Situazione diversa con polarizzazione esterna
Equilibrio:
La barriera di potenziale (← Campo elettrico dovuto alla carica spaziale)
e' quella di built-in
Polarizzazione inversa:
Situazione simile, con barriera piu' alta
V = Vbi + Vext
Polarizzazione diretta:
Situazione simile, con barriera piu' bassa
V = Vbi −Vext