MATEMATICA CORSO A
SCIENZE BIOLOGICHE
COMPITO PROVA 2
II PROVA IN ITINERE
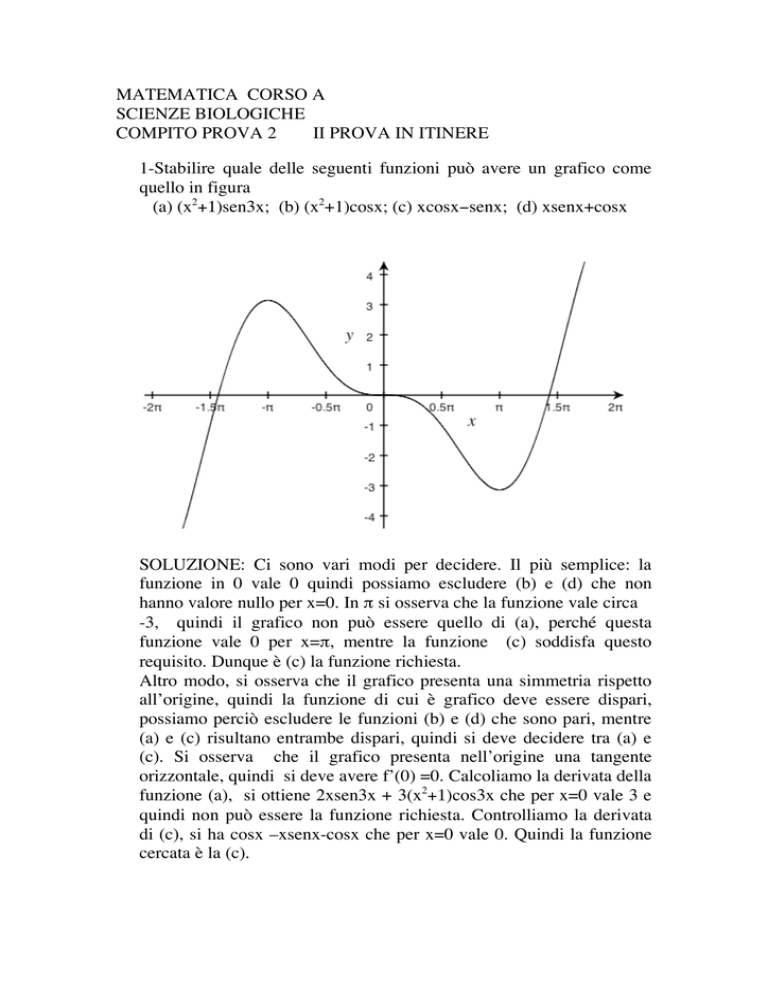
1-Stabilire quale delle seguenti funzioni può avere un grafico come
quello in figura
(a) (x2+1)sen3x; (b) (x2+1)cosx; (c) xcosx−senx; (d) xsenx+cosx
SOLUZIONE: Ci sono vari modi per decidere. Il più semplice: la
funzione in 0 vale 0 quindi possiamo escludere (b) e (d) che non
hanno valore nullo per x=0. In π si osserva che la funzione vale circa
-3, quindi il grafico non può essere quello di (a), perché questa
funzione vale 0 per x=π, mentre la funzione (c) soddisfa questo
requisito. Dunque è (c) la funzione richiesta.
Altro modo, si osserva che il grafico presenta una simmetria rispetto
all’origine, quindi la funzione di cui è grafico deve essere dispari,
possiamo perciò escludere le funzioni (b) e (d) che sono pari, mentre
(a) e (c) risultano entrambe dispari, quindi si deve decidere tra (a) e
(c). Si osserva che il grafico presenta nell’origine una tangente
orizzontale, quindi si deve avere f’(0) =0. Calcoliamo la derivata della
funzione (a), si ottiene 2xsen3x + 3(x2+1)cos3x che per x=0 vale 3 e
quindi non può essere la funzione richiesta. Controlliamo la derivata
di (c), si ha cosx –xsenx-cosx che per x=0 vale 0. Quindi la funzione
cercata è la (c).
2- Può esistere una funzione periodica di periodo 7 e tale che
f(0)=500? Se sì, fai un esempio, se no, spiega perché.
SOLUZIONE: Sì può esistere, ad esempio f(x)=500cos[(2π/7)x]
3-E’ assegnata una funzione f(x) sulla quale sono noti i fatti
seguenti:dominio D ={∀x∈R : x≠±2}
limx→+∞f(x) = 0 , limx→2-f(x) = − 2, limx→2+f(x) = 2
f(x) è dispari, continua e derivabile e si ha
f’(x) < 0 per 0≤x<2, oppure x>2
a) disegnare un grafico approssimativo di f(x)
b) disegnare un grafico di f(x-2)
4- Assegnata la funzione f(x) = [log2x - 1] / log2(3x+1)
Determinare
a) dominio della funzione
b) eventuali x tali che f(x)=0
c) eventuali x tali che f(x)<0
SOLUZIONE:a) si deve avere x>0 affinchè sia definita log2x, inoltre si
deve imporre 3x+1>0 affinchè sia definita log2(3x+1), la quale deve
anche essere ≠0, quindi 3x+1≠1, tenuto conto di queste condizioni, il
dominio risulta essere definito per x>0; b) f(x)=0, se si annulla il
numeratore, vale a dire log2x – 1=0, quindi log2x = 1, quindi x=2;
c) si avrà f(x)<0 se numeratore e denominatore hanno segno discorde; si
osserva che il numeratore è positivo per x>2, mentre il denominatore è
positivo per 3x+1>1, quindi per x>0, per cui il denominatore risulta
positivo su tutto il dominio di f(x), concludendo si avrà f(x)<0 quando il
numeratore è minore di 0, perciò per 0<x<2.
5- Calcolare la derivata della funzione log(x3 – 3x) e determinare gli
eventuali punti di massimo o minimo relativo della funzione.
SOLUZIONE:
Studiamo il dominio della funzione f(x)= log(x3 – 3x). Si deve avere che
x3 – 3x>0, vale a dire x(x2 – 3)>0 e quindi
{x∈R: -√3<x<0}∪{x∈R:x>√3}
Calcoliamo la derivata, si ha f’(x)=(3x2 – 3)/(x3 – 3x) e il suo segno è
determinato dal segno del numeratore in quanto, f(x) è definita solo per
x3 – 3x >0 e quindi il denominatore di f’(x) è sempre positivo. Dunque
f’(x)>0 per -√3<x<-1 oppure x>√3 e quindi in tali intervalli f(x) risulta
crescente, mentre f’(x)<0 per -1<x<0, dove f(x) risulta decrescente,
poiché f’(-1)=0, f(x) ha in x=-1 un punto di massimo relativo, dove
assume valore log2.
6 - Una popolazione di cellule tumorali N cresce, in funzione del tempo t,
secondo la legge
2
N(t) = 103 exp3(1 − exp(−0.6t))
Dove con exp si è indicata la funzione esponenziale con base la
costante di Nepero e.
Studiare la funzione N(t) (anche per t negativi) e disegnarne un
grafico.
SOLUZIONE: La funzione è definita su tutta la retta reale ed è sempre
positiva. Calcoliamo il limite per t→−∞, exp(−0.6t) tende a +∞,
−exp(−0.6t) tende quindi a − ∞, quindi N(t) tende a 0. Calcoliamo il
limite per t→+∞, exp(−0.6t) tende a 0, 1−exp(−0.6t) tende quindi a 1,
quindi N(t) tende a 103exp(2/3).
La funzione N(t) risulta crescente in quanto composizione di funzioni
crescenti(essendo exp(-0.6t) decrescente e quindi –exp(-0.6t) crescente),
controlliamo comunque attraverso lo studio del segno della derivata
prima, si ha
2
N’(t) = 103 exp3(1 − exp(−0.6t)) 2/3(0.6)exp(−0.6t) >0
Da quanto trovato appare chiaro che ci deve essere un cambio di
concavità e quindi un punto di flesso, vediamo di individuarlo attraverso
lo studio del segno della derivata seconda
2
N”(t)=103 exp3(1 − exp(−0.6t)) (2/3(0.6)exp(−0.6t))2 −
2
− 103 exp3(1 − exp(−0.6t)) (2/3(0.6)2 exp(−0.6t)=
2
= 103 exp3(1 − exp(−0.6t)) (2/3(0.6)2exp(−0.6t))(2/3exp(−0.6t) –1)
Quindi si ha N”(t) = 0 per t*= ln(2/3) /(0.6) = 5/3 ln(2/3) , dove si ha un
punto di flesso ; essendo N”(t) >0 per t<t* , la funzione è convessa per
t<t* , ed N”(t)<0 per t>t* dove la funzione è concava. Si osserva che il
flesso si ha per un valore di t<0 , essendo ln(2/3)<0 , quindi
all’osservazione (per t>0) la curva di crescita risulta concava.
OSSERVAZIONE: Questa funzione è nota come funzione di Gompertz
ed ha avuto molta influenza negli studi, non solo teorici, in campo
oncologico. Si adatta molto bene ai dati empirici di crescita di molti
tumori.