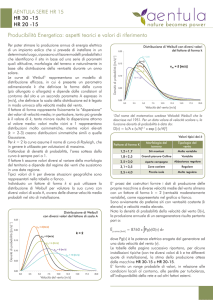
DISTRIBUZIONE DI WEIBULL
La funzione di densità di probabilità della legge di distribuzione di Weibull, f(H) risulta
completamente definita da tre parametri:
- il fattore di scala b;
- il fattore di posizione x0 ;
- il fattore di forma k.
k H x0
f (H )
b b
k 1
H x0 k
exp
b
con
k > 0, b > 0 e H ≥ x0 ≥ 0
Secondo questa legge, la probabilità di eccedenza P(H) risulta essere:
H x0 k
P( H ) exp
b
Ponendo x0 = 0 si definisce la distribuzione di Weibull a 2 parametri.
H k
P( H ) exp
b
La distribuzione di Weibull è legata ad una serie di distribuzione di probabilità, in particolare
interpola la distribuzione esponenziale (se k = 1) e la distribuzione di Rayleigh (se k = 2).
Si riportano degli esempi che servono a confronto dell’andamento della P(H) al variare dei
parametri.
In Figura 1 si mantiene costante il fattore di scala facendo variare il fattore di forma, contrario
avviene invece in Figura 2.
1.0E+000
b = cost
Probability of Exceedance , Pex(H)
k=1
k=1.5
k=2
k=2.5
1.0E-001
1.0E-002
1.0E-003
0
5
10
15
H
Fig. 1: Probabilità di eccedenza secondo distribuzione Weibull al variare del fattore di forma
1.0E+000
k = cost
Probability of Exceedance , Pex(H)
b=1
b=2
b=3
b=4
1.0E-001
1.0E-002
1.0E-003
0
5
10
15
H
Fig. 2: Probabilità di eccedenza secondo distribuzione Weibull al variare del fattore di scala
STIMA DEI PARAMETRI
Esistono diversi modi per stimare i parametri caratteristici della distribuzione, essi sono divisibili in
2 categorie: metodi grafici e metodi analitici.
Metodi grafici:
essendo F(H) la probabilità cumulata di non superamento:
H k
F ( H ) 1 P( H ) 1 exp
b
risulta essere:
H k
1 F ( H ) exp
b
H k
1
exp
1 F (H )
b
H
1
ln
1 F ( H ) b
k
1
ln ln
k ln H k ln b
1 F ( H )
L’ultima equazione è quella di una retta, per plottare F(H) rispetto H si usa la seguente procedura:
1) Si ordina il campione in ordine ascendente;
2) Si stima F(Hi) tramite uno dei metodi illustrati in Tabella 1 (n = popolazione del campione).
METHOD
Mean Rank
Median Rank
Symmetrical CDF
Tabella 1: Metodi per la stima di F(Hi)
F(Hi)
i
n 1
i 0. 3
n 0.4
i 0.5
n
Metodi analitici:
In questa categoria esistono diversi metodi:
-
metodo della massima verosimiglianza (MLE: Maximum Likelihood Estimator);
metodo dei momenti (MOM: Method of Moments);
metodo dei minimi quadrati (LSM: Least Squares Method).
Si illustra solamente l’ultimo metodo che risulta essere quello più semplice.
Ci si riferisce all’equazione lineare già vista nel metodo grafico:
1
ln ln
k ln H k ln b
1 F ( H )
Si può inoltre scrivere:
1
1
H ln ln
i
n i 1
1
n 1
n
Y
1 n
ln ( H i )
n i 1
Ne segue:
n
n
n
1
1
n
ln(
H
)
ln
ln
ln(
H
)
ln
ln
i
i
i
i
i 1
1
i 1
1
i 1
n 1
n 1
ˆk
2
n
n
2
n ln( H i ) ln( H i )
i 1
i 1
Y H
bˆ exp
kˆ