Il test chi quadro e la relativa distribuzione

Il test chi quadro e la relativa
distribuzione
V.a. chi quadro a k gradi di libertà
0.06
0.04
0.00
0.02
dchisq((0:1000)/30, 10)
0.08
0.10
Definition La somma dei quadrati di k v.a. gaussiane standard indipendenti si chiama
v.a. chi quadro a k gradi di libertà:
X k := Z 21 + ... + Z 2k .
0
5
10
15
20
25
30
(0:1000)/30
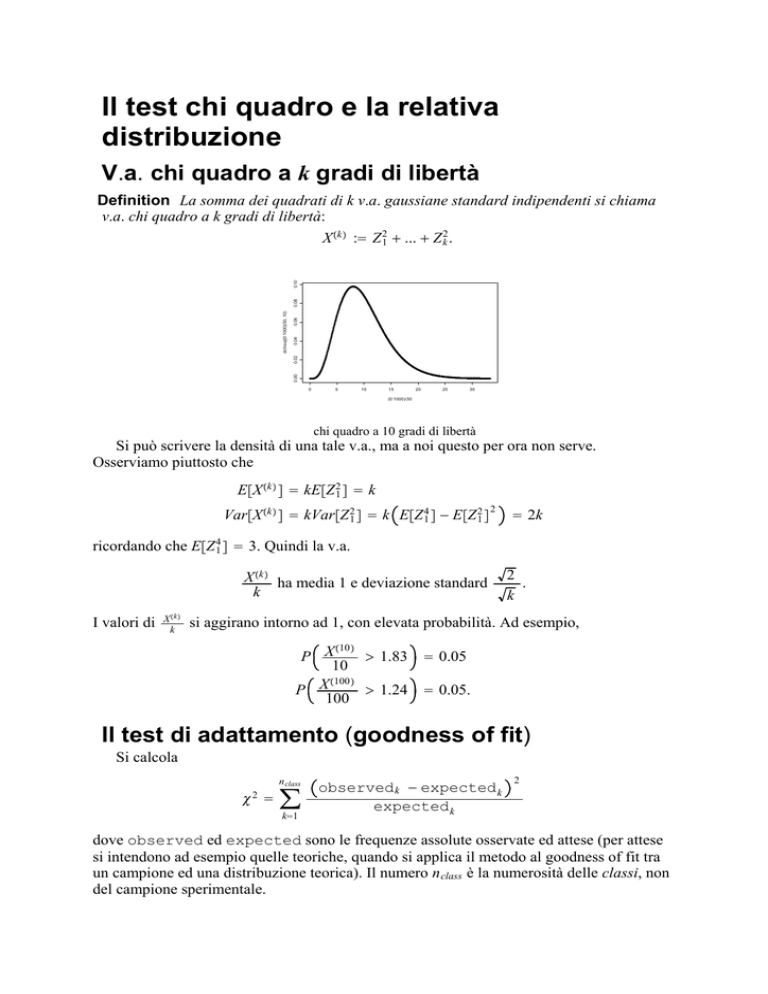
chi quadro a 10 gradi di libertà
Si può scrivere la densità di una tale v.a., ma a noi questo per ora non serve.
Osserviamo piuttosto che
EX k  = kEZ 21  = k
VarX k  = kVarZ 21  = k EZ 41  − EZ 21 
2
= 2k
ricordando che EZ 41  = 3. Quindi la v.a.
X k ha media 1 e deviazione standard
k
I valori di
X k
k
2
.
k
si aggirano intorno ad 1, con elevata probabilità. Ad esempio,
10
P X
> 1.83
10
100
P X
> 1.24
100
= 0.05
= 0.05.
Il test di adattamento (goodness of fit)
Si calcola
n class
χ =
2
∑
k=1
observed k − expected k
expected k
2
dove observed ed expected sono le frequenze assolute osservate ed attese (per attese
si intendono ad esempio quelle teoriche, quando si applica il metodo al goodness of fit tra
un campione ed una distribuzione teorica). Il numero n class è la numerosità delle classi, non
del campione sperimentale.

Se abbiamo le probabilità empiriche p e quelle teoriche p, di una distribuzione discreta
o di una continua discretizzata mediante classi, ed N indica la numerosità del campione,
class
vale χ 2 = ∑ k=1
n

p k ⋅N − p k ⋅N
p k ⋅N
2
, ovvero
n class
χ2 = N ∑

2
p k − pk 
.
pk
k=1
Si dimostra che, se il campione sperimentale proviene dalla distribuzione teorica
(ipotesi nulla), questa variabile aleatoria tende per N → ∞ ad una distribuzione chi quadro a
n class − 1 gradi di libertà. La ragione risiede nel teorema limite centrale, come spiegano in
parte le seguenti due note.
Remark La dimostrazione non è elementare. Capiamo però alcuni elementi quantitativi.


 p −p  2
Sembra infatti strano che nella definizione di χ 2 compaia k p k k invece che  p k − p k  2

2
 p −p 
(errore quadratico assoluto) oppure k p 2 k (errore quadratico relativo). Per il teorema
k
limite centrale
observed k − Np k
Np k 1 − p k 
→ Z k gaussiana canonica
N→∞
quindi
observed k − expected k
expected k
2
→ Z 2k ⋅ 1 − p k .
N→∞
Da qui però non è chiaro come mai si perda un grado di libertà e spariscano i coefficienti
1 − p k .
Remark Esaminiamo però il caso n class = 2: siccome
obs 2 − exp 2
exp 2
2
=
N − obs 1 − N − exp 1 
N − exp 1 
=
obs 1 − exp 1
N − exp 1 
2
2
vale
χ2 =
obs 1 − exp 1
exp 1
2
obs 1 − exp 1
exp 1
2
+
obs 1 − exp 1
N − exp 1 
2
1
→ Z2.
1 − p k N→∞ 1
In un colpo solo si vede che si perde un grado di libertà e spariscono i fattori
moltiplicativi.
Se la distribuzione empirica differisce troppo da quella teorica, χ 2 assume valori troppo
grandi rispetto al suo normale. Fissata la significatività α, si deve allora cercare quel
numero λ α,n class tale che una chi quadro a n class − 1 gradi di libertà lo supera con
probabilità α:
=
⋅
PX n class −1 > λ α,n class  = α.
Come visto sopra, può essere più naturale l’uso di
χ2
n class −1
, che tende alla distribuzione
X
n class −1
n class −1
per N → ∞. Ad esempio,
χ2
> 1.83
n class − 1
χ2
= 111 : si rifiuta l’ipotesi se
> 1.24
n class − 1
per n class = 11 : si rifiuta l’ipotesi se
per n class
a livello di significatività α = 0.05. Rifiutare l’ipotesi significa affermare che il campione
non segue le probabilità teoriche specificate.
In realtà nei SW non si specifica mai α, ma si calcola il valore p. Se si trova un valore
p < 0.05, si rifiuta l’ipotesi. Nei test di adattamento, come il chi quadro o Kolmogorov
Smirnov, la lettura intuitiva dell’output di R è:
p molto piccolo ⇒ il campione non segue la legge.
Altrimenti, non si ha motivo di rifiutarla.
Test chi quadro in relazione a metodi basati sulla
varianza
Non entriamo in dettagli ed esempi ma osserviamo solamente che in vari problemi di fit
di modelli, cioè di relazioni tra fattori X i e risposte Y j , come l’analisi fattoriale o
ANOVA, l’errore che si commette nel fit è legato a somme di quadrati di gaussiane
indipendenti, quindi legato a variabili chi quadro. Più precisamente, l’errore  2 che si
commette nel fit (o qualche grandezza ad esso collegata) è chi quadro se il campione
proviene dal modello. Si applicano allora ragionamenti simili ai precedenti: fissato
α = 0.05 (ad esempio), si confronta  2 con una soglia calcolata come sopra e se  2 supera
la soglia, si rifiuta l’ipotesi, cioè si afferma che il campione non proviene da quel modello,
ovvero si ritiene cattivo il fit. Se si calcola il valore p, se p < 0.05 si rifiuta l’ipotesi, cioè
come appena detto si ritiene cattivo il fit.