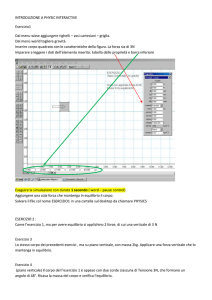
Come si trova il punto di applicazione di R ?
Tanto la retta di azione quanto il punto di applicazione della risultante del
sistema non sono determinabili attraverso la somma dei vettori effettuata con il
metodo di punta-coda o del parallelogramma. Tale tecnica, che consente di
sommare vettori, cioè classi di equivalenza di segmenti equipollenti, fornisce
soltanto l’intensità del risultante ed una direzione, quella della diagonale del
parallelogramma, alla quale il risultante è parallelo, ma non il punto di
applicazione1. Tuttavia il risultante del sistema di forze deve avere lo stesso
momento del sistema stesso, quindi se esiste un punto sull’oggetto rispetto al
quale la somma dei momenti è nulla, il risultante applicato in modo che abbia
momento zero rispetto quel punto sostituisce interamente il sistema di forze.
Esempio 2
Trovare, se esiste, il punto (od i punti) in cui si può applicare il risultante del
sistema di forze FA ed FB , di pari intensità, che agiscono sul quadrato in figura.
Dopo aver tracciato le rette di azione delle forze si riconosce che una forza ha sempre
momento nullo rispetto ad un qualunque asse che passa per la sua retta di azione.
Quindi entrambe le forze devono avere momento nullo rispetto ad un asse
perpendicolare al foglio nel punto P, intersezione delle due rette di azione. Ne segue
che anche il risultante dovrà avere momento nullo rispetto a P, quindi la sua retta
d’azione (inclinata di 45° rispetto al lato del quadrato visto che le forze hanno la
stessa intensità), dovrà passare per P. Quindi il risultante può essere applicato in uno
qualunque dei punti in cui la retta a 45° passante per P intercetta il quadrato.
FB
FA
R
FB
FA
P
FC
FD
Esempio 3
Trovare, se esiste, il punto di applicazione del sistema di forze parallele FC ed FD ,
FC
che agiscono sul quadrato in figura.
Le rette di azione delle due forze parallele non si incontrano mai, tuttavia è possibile
operare sommando al sistema due forze opposte che non alterano la dinamica
perché hanno risultante nullo (in verde nella figura). In questo modo si ottiene il
punto P rispetto al quale il sistema ha momento nullo, e così si fa passare per P la
retta di azione del risultante la cui direzione è ottenuta con la regola del
parallelogramma. Il risultante potrà poi essere applicato in uno qualunque dei punti
in cui la retta trovata intercetta il corpo, per esempio sul bordo del quadrato.
Esempio 4
Trovare il punto (od i punti) in cui si può applicare il risultante del sistema di forze
FA ed FB , di pari intensità, che agiscono sulla lamina in figura.
La direzione del risultante si trova con la tecnica del parallelogramma: lungo una
retta parallela a quella rossa tratteggiata. Per individuare il punto di applicazione di
Per sommare vettori applicati occorre operare la costruzione del cosiddetto poligono
funicolare, il quale consente di conoscere la retta di azione del risultante, e, se reiterato su
di un sistema di forze ruotato rispetto all’originale, anche il punto di applicazione.
1
5
R
FD
P
FB
R
P
FA
R , dopo aver tracciato le rette di azione delle forze si riconosce che il sistema ha
momento nullo rispetto al punto in cui le due rette si incontrano. Pertanto il
risultante potrà essere applicato in uno qualsiasi dei punti in cui la retta rossa
tratteggiata incontra la lamina, ad esempio P.
FA
b
FA
Cosa si intende per coppia di forze?
Un sistema molto semplice di forze è quello qui a fianco illustrato, denominato
coppia. Esso è costituito da due forze di pari intensità, parallele ma dirette in
versi opposti: il suo risultante è chiaramente nullo. Il momento di una coppia
indica la sua capacità di far ruotare un qualunque segmento, solidale con il
corpo, e perpendicolare alle rette di azione delle forze, come quello
rappresentato da b in figura. Ai fini dell’equilibrio (o del moto) di un corpo
rigido, sono equivalenti due coppie aventi lo stesso momento, come ad
esempio le FA , FA e FB , FB in figura, con FA FB .
FB
Quanto vale il momento di una coppia di forze?
E’ possibile dimostrare che, qualunque sia l’asse che si sceglie, sebbene il
momento di ciascuna forza rispetto ad esso vari con l’asse, il momento
risultante della coppia sarà sempre dato dal prodotto dell’intensità comune,
F , per la distanza fra le rette di azione, b, detto anche braccio della coppia:
b
FB
Fb
Come si può individuare un semplice sistema di forze equivalente ad uno dato?
Si può dimostrare che l’azione di un sistema di forze complanari su di un corpo
rigido libero di muoversi di moto piano, è sempre equivalente a quella del
F
E’ possibile spostare una forza lungo la sua retta di azione?
C
F
B
F
A
risultante R del sistema, applicato in un punto P scelto arbitrariamente,
insieme a quella di una coppia di forze che abbia, rispetto ad un asse
perpendicolare al piano e passante per P, lo stesso momento risultante del
sistema.
Un conseguenza della proprietà suesposta è la possibilità di spostare una forza F
lungo la sua retta di azione senza conseguenze per la dinamica del corpo. In questo
modo infatti non si altera né la risultante del sistema di forze né il suo braccio, e
quindi non ne viene modificato nemmeno il valore del momento totale rispetto
ad un qualunque asse. Ad esempio, riferendoci alla figura a lato, è del tutto
indifferente ai fini del moto del triangolo, applicare F in A, B oppure in C.
In quali altri modi si può spostare una forza senza alterare la dinamica del corpo?
Esiste una tecnica che consente di spostare una forza F , applicata in un punto A, in
un punto diverso, B, facendo in modo che F si mantenga parallela alla sua retta di
azione. Infatti, se la nuova forza è parallela alla vecchia, il risultante del sistema di
forze che agisce sul corpo non viene alterato: l’unica cosa che cambia è il momento
risultante. Basterà allora compensare il cambiamento che l’operazione di
6
spostamento comporta sul momento risultante. A tale scopo si dovrà applicare al
corpo una coppia di trasporto, intendendo con ciò una qualsiasi coppia di forze che
abbia, rispetto ad un asse passante per il nuovo punto di applicazione B, lo stesso
A
momento che aveva prima F quando era applicata in A. Considerando la figura, si
vede bene come la coppia di forze FA FB , ciascuna di intensità pari a quella F ,
compensi la modifica che lo spostamento del punto di applicazione di F da A in B
B
F
ha comportato per il momento risultante. Ma per la prima proprietà sopra enunciata,
tutte le coppie di uguale momento sono equivalenti, e quindi si potrà usare come
FB
coppia di trasporto una qualunque coppia equivalente alla FA FB , ad esempio la
FC FD con FC FD F .
b
A
FA
B
F
FD
b
A
FC
7
B
F
3. Equilibrio di un corpo rigido
Scelto quindi un asse, ed indicato con P il punto in cui questo buca il piano, per
vedere l’effetto di un sistema di forze su di un corpo si deve applicare il risultante
R in P e far agire una qualunque coppia di momento pari al momento risultante
. Se in particolare R e sono nulli, il sistema di forze non può modificare lo stato
di quiete (o di moto rettilineo uniforme) del corpo, e pertanto:
Diremo che un corpo rigido si trova in una condizione compatibile con l’equilibrio se
sono contemporaneamente nulli il risultante ed il momento risultante del sistema di
forze che agiscono su di esso.
FA
F
i
A
B
FB
FA
A
10 m
F (14 N)
Esempio 1
Il blocco rigido in figura è in equilibrio sotto l’azione di un certo numero di forze, fra
cui FA ed FB che hanno uguale valore. Si dica se il corpo resterebbe in equilibrio nel
caso in cui, a parità di ogni altra circostanza, FA ed FB venissero applicate
Il momento di F rispetto a B è
FB (28 N)
10 m
B
5m
FA(28 N)
2N
3m
A
0
Esempio 2
Il triangolo ABC è in equilibrio ed una delle forze agenti è indicata in figura. Senza
modificare l’equilibrio si trasli tale forza nel punto B individuando il modulo delle
forze di una coppia di trasporto costituita da forze orizzontali applicate in A e in B.
A
1N
i
i
B
5m
A
Si, resterebbe in equilibrio perché una coppia di forze verrebbe sostituita da una
coppia di momento uguale, anche se non complanare, e quindi senza alterare
l’equilibrio di un corpo rigido.
B
C
i
rispettivamente nel vertice A e nel vertice B.
FB
C
0
5m
C
F Fb 14 10 140 N m (antiorario).
Per ottenere lo stesso valore con una coppia di forze orizzontali applicate in A verso
destra ed in B verso sinistra deve essere:
FA 5 140 ,
da cui:
FA 28 N .
Esempio 3
Si dica se è possibile che il segmento rigido AB sia in equilibrio sotto l’azione di
B
quattro forze: le tre disegnate più un’altra. (Per la risoluzione considerare i momenti
3 N rispetto a C.)
8
15 m
Non è possibile. Infatti la forza necessaria per l’equilibrio dovrebbe avere un
componente verticale di 1N verso l’alto ed un componente orizzontale di 1N verso
destra. Inoltre, per l’equilibrio della rotazione attorno a C (rispetto a cui le forze da
1N e 2N hanno momento nullo), si deve produrre un momento uguale e contrario a:
1N
C
1N
3N 5m 15 N m (che è orario).
A
Il componente orizzontale da 1N verso destra ha momento nullo rispetto a C dato
che la sua retta di azione passa per tale punto. Per equilibrare 15 N m dovrei
B
allora applicare il componente verticale da 1N verso il basso in un punto 15 metri a
sinistra di C, cosa impossibile perché il punto cadrebbe fuori dal segmento.
C
4N
4N
Esempio 4
La lamina rigida triangolare ABC è in equilibrio sotto l’azione di tre forze, due delle
quali sono rappresentate in figura. Si dica se è possibile che la terza forza sia
applicata nel punto medio del lato BC.
Non è possibile perché le due forze hanno momento nullo rispetto al punto A e
quindi dovrà essere nullo anche il momento delle terza forza rispetto ad A. Ciò
implica che la sua retta d’azione debba passare per A. Essendo poi le due forze
uguali, la retta d’azione è la bisettrice dell’angolo A e quindi la terza forza sarà
applicata in uno dei punti in cui la bisettrice incontra il triangolo (ad esempio quello
indicato), e quindi il punto medio di BC è escluso.
Esempio 5
La lamina rigida trapezoidale è in equilibrio sotto l’azione di tre forze, due delle
quali sono indicate in figura, applicate nei punti A e C. Si dica se è possibile
individuare retta di azione e punto di applicazione della terza forza nel caso in
A
B
C
A
F2
B
F1
esame, e nel caso in cui F1 abbia verso opposto.
Nel primo caso la retta di azione di F3
deve essere parallela alla diagonale del
parallelogramma di F1 ed F2 . Inoltre, dato che F1 ed F2 hanno momento nullo
F2
rispetto al punto B, deve passare per B. L’unico punto che appartiene al trapezio e
che sta sulla retta di azione individuata è proprio B. Nel secondo caso vi sono infiniti
punti sul trapezio che appartengono alla retta di azione di F3 e quindi il punto di
applicazione è indeterminato
B
F1
F3
F2
B
9
F1
C
4. Il baricentro di un corpo rigido
Se un corpo rigido è soggetto all’azione di un sistema di forze, per
conoscerne gli effetti sul moto, dovremo eseguire il calcolo del momento risultante
, per via diretta, sommando i momenti di tutte le forze coinvolte, e del
risultante R , applicando il metodo di punta coda in sequenza.
Una semplificazione è tuttavia possibile nel caso in cui il sistema sia costituito da
forze tutte parallele, come accade nel caso delle forze dovute alla gravità, che
agiscono in direzione verticale su ciascuno dei punti materiali che compongono un
corpo rigido. In questo caso infatti è possibile dimostrare che esiste punto, detto
centro del sistema di forze, che ha la notevole proprietà per cui:
applicare un sistema di forze parallele ad un corpo rigido è equivalente, ai fini
dell’equilibrio (o del moto), ad applicare il solo risultante R nel centro del sistema
di forze, qualora questo cada all’interno del corpo.
A
FA
G
bB
bA
B
R
FB
Come si può determinare tale centro?
Applicare un sistema di forze ad un corpo rigido è equivalente ad applicare il suo
risultante in un qualunque punto P insieme ad una coppia che abbia per momento il
momento risultante rispetto all’asse che passa per P. Nel caso di un sistema di forze
parallele, dovremo quindi trovare il punto dove applicare il risultante in modo che
equivalga, da solo, all’intero sistema. Questo accade se è nulla la somma dei momenti
rispetto all’asse perpendicolare al foglio e passante per il punto di applicazione. In
questo modo infatti sarà nullo anche il momento della coppia che avremmo dovuto
affiancare al risultante, che è proprio quello che si sta cercando di ottenere.
Analizziamo il caso semplice di un sistema di due sole forze parallele ed equiverse, e
consideriamo il loro momento risultante rispetto ad un asse che si trovi fra le loro
rette di azione e sia perpendicolare al piano del foglio. Consideriamo la
congiungente AB dei punti di applicazione delle due forze FA ed FB : per effettuare
il calcolo con semplicità prenderemo un asse che intercetta AB, ma si può dimostrare
che il risultato non cambia se si trasla l’asse parallelamente alle rette di azione delle
due forze. Indichiamo con G il punto in cui l’asse buca il piano. Cerchiamo quindi
quale deve essere la distanza di G da A affinché valga zero la somma dei momenti:
| FA | bA | FB | bB 0
dove il segno meno tiene conto del fatto che FB tende a far ruotare in verso
orario attorno a G. In un riferimento cartesiano avremo bA xG x A e
bB x B xG da cui:
| FA | (xG x A ) | FB | (x B xG ) 0
10
xG (| FA | | FB |) x A | FA | x B | FB |
x A | FA | x B | FB | x AFA x B FB
xG
FA FB
|R |
dove, essendo le forze parallele si è sfruttato il fatto che l’intensità del risultante
è data semplicemente dalla somma delle intensità: | R || FA | | FB | . Ne
concludiamo che ponendo l’asse G lungo una qualunque retta verticale avente
per ascissa il valore xG trovato, il momento risultante del sistema di forze
rispetto ad esso sarà nullo. Per trovare anche l’ordinata del punto G, torniamo
alla relazione | FA | bA | FB | bB 0 , che riscriviamo come:
| FA | bB
GB
| FB | bA
AG
A
G
bB
K
H bA
B
dove l’ultima uguaglianza si deve alla similitudine dei triangoli rettangoli
AHG e BKG.
Immaginiamo ora di avere un altro sistema di forze, ottenuto ruotando
quello originario di un angolo qualunque attorno al loro punto di applicazione.
Poiché né la lunghezza del segmento AB , né le intensità delle forze sono
cambiate, il centro G di questo secondo sistema soddisferà ancora la relazione
| FA |
GB
. Ciò implica che nemmeno GB e AG mutano, in quanto si
| FB |
AG
mantengono uguali sia la loro somma che il loro rapporto. Se ne conclude che il
centro G del il sistema ruotato è lo stesso di quello originario. Il risultante, che si
può pensare applicato in G, ruoterà anch’esso dello stesso angolo attorno al suo
punto di applicazione.
Possiamo allora ricavare la coordinata yG del centro del sistema
FA
A
R
G
B
ruotando le forze di 90° e ripetendo il ragionamento sul nuovo sistema:
yA | FA | y B | FB | yAFA yB FB
yG
FA FB
|R |
Se ne conclude che G si trova sul segmento AB congiungente i punti di
applicazione delle due forze, a distanze da A e da B inversamente proporzionali
alle intensità delle forze stesse.
Come si calcola il centro delle forze parallele dovute alla gravità?
Possiamo immaginare la forza di gravità come un sistema di N forze parallele,
che agiscono su ciascuno degli atomi puntiformi che costituiscono un corpo
rigido. Il ragionamento sopra permette di concludere che per ogni corpo
rigido esiste un punto G, detto baricentro, di coordinate:
m1g
m 3g
m 2g
11
FB
x f
f
x m g
m g
y f
f
y m g
m g
i i
xG
i
i
i
i i
yG
i
i
i
i
i
i
i
m1x1 m2x 2 ... mN x N
m1 m2 ... mN
i
i
i
i
i
m1y1 m2y2 ... mN yN
m1 m2 ... mN
i
rispetto al quale la somma dei momenti delle forze risulta zero. Le forze di
gravità che agiscono su ciascuna delle particelle che compongono il corpo non
hanno quindi la capacità di farlo ruotare attorno al suo baricentro, e pertanto G
è il punto in cui può pensarsi applicato il risultante.
Si dice baricentro di un corpo il punto in cui può pensarsi applicata la forza di
gravità
G
Il baricentro è un punto che appartiene al corpo?
Sebbene le coordinate di G siano in ogni caso interne ad un rettangolo
individuato dalla massima e minima ascissa (rettangolo rosso in figura), e dalla
massima e minima ordinata dei punti, G può anche cadere fuori dal corpo. Un
semplice esempio di questo caso si ha per un oggetto a forma di ciambella,
oppure una bottiglia vuota. Nel caso in cui G sia interno al corpo potremo
effettivamente sostituire all’intero sistema di forze il suo risultante applicato in
G. Nel caso in cui sia esterno, potremo comunque utilizzarlo come punto
immaginario di applicazione delle forze di gravità al fine di semplificare alcuni
calcoli, come ad esempio il momento della gravità rispetto ad un qualunque
altro asse, oppure il calcolo del lavoro della forza di gravità.
12
5. Determinazione del baricentro
m
Sistemi discreti
G
Le formule dirette per il calcolo delle coordinate del baricentro di un corpo sono
di immediata applicazione nel caso esso sia costituito da un sistema di punti.2
Vediamo alcuni esempi.
m
Una coppia di masse puntiformi uguali.
xG
x 1mg x 2mg
x x2
1
;
mg mg
2
yG
y1mg y2mg
y y2
1
mg mg
2
come si vede il baricentro si trova a metà strada fra le due masse, posto sul
segmento che le congiunge.
Una coppia di masse puntiformi differenti
mA
Anziché fare il calcolo diretto desumeremo informazioni ponendo l’asse x
lungo la congiungente e l’asse y passante per G. Avremo xG 0 e y G 0 ,
mB
G
dA
dB
però se con d A e d B si indicano le distanze di G dalle masse risulta:
xG
dAmA dB mB
0
mA mB
mA
d
B
mB
dA
cioè il baricentro è più vicino alla massa più pesante fra le due. Se ad esempio si
hanno due punti di cui uno pesa tre volte l’altro risulterà:
xG
x Am 3x B m
x 3x B
A
m 3m
4
o anche:
dB
1
, cioè la distanza da A è tre volte quella da B.
dA
3
Una struttura di masse puntiformi differenti
m1
Se non vi sono simmetrie, note le coordinate in un riferimento opportuno, e
note le masse, si applica direttamente la definizione:
xG
x 1m1 x 2m2 x 3m 3 x 4m 4 x 5m5
m1 m2 m 3 m 4 m5
yG
y1m1 y2m2 y 3m 3 y 4m 4 y5m 5
m1 m2 m 3 m 4 m5
2
m2
m3
m4
Detto anche sistema discreto
13
m5
Sistemi continui
G
Nel caso di sistemi continui non è possibile utilizzare nella pratica la formula
per punti, tuttavia vale la proprietà seguente:
Proprietà distributiva del baricentro: il baricentro di un corpo si può ottenere
suddividendolo in elementi ed immaginando la massa di ciascuno concentrata
nel proprio baricentro.
Una sbarretta omogenea
Applicando la proprietà distributiva la possiamo vedere come una serie di
coppie di masse puntiformi uguali. Avendo ciascuna coppia il baricentro nel
punto medio, quella sarà anche la posizione di G della sbarretta
Un corpo dotato di un asse di simmetria
Se una figura piana ha un asse di simmetria possiamo immaginare di
suddividerla in tante sbarrette con centro di simmetria su quell’asse. Con
questo approccio estendiamo facilmente il risultato precedente per cui il
baricentro si troverà sicuramente sull’asse di simmetria.
Se gli assi di simmetria sono più di uno, allora ripetendo il ragionamento
troviamo che G giacerà sul loro punto di incontro. E’ il caso di un quadrato, un
cerchio, un anello, il cui baricentro sarà nel loro centro geometrico. Se il corpo
ha tre dimensioni il ragionamento si può ripetere per cui risulta che corpi solidi
regolari come sfere, cilindri o parallelepipedi retti hanno il baricentro nel punto
di incontro dei loro assi di simmetria.
C
Un triangolo pieno
Una lamina piana a forma di triangolo si presta ad un calcolo del baricentro
tramite suddivisione in barrette parallele ad uno dei lati. Ognuna di esse avrà il
suo baricentro nel punto medio, pertanto anche il baricentro del triangolo
giacerà sul segmento comune a tutti i punti medi e cioè la mediana del lato a cui
le barrette sono parallele. Ripetendo il ragionamento per un altro lato si
dimostra così che il baricentro si trova nel punto di incontro delle mediane.
G2
G
B
Tre masse uguali nei vertici di un triangolo
Osserviamo che un risultato analogo vale per un triangolo costituito da tre
masse uguali poste nei suoi vertici. In questo caso possiamo applicare la
proprietà distributiva sostituendo alle masse A e B una massa pari alla loro
somma ma posta nel loro baricentro, cioè nel punto medio del lato. Sappiamo
ora che il baricentro del sistema dei due punti C ed A+B giace sulla loro
congiungente, che in questo caso è la mediana del lato AB. Ripetendo il
ragionamento per un’altra coppia è dimostrato che il baricentro si trova sul
punto d’incontro delle mediane.
G1
A
G1
G4
G3
G2
Baricentro di un generico quadrilatero pieno
Basterà dividere il quadrilatero in due triangoli unendo con un segmento due
suoi vertici non consecutivi. Sostituendo poi ciascuno dei due triangoli con una
massa puntiforme posta nel suo baricentro, ovvero nel punto di incontro delle
mediane, ne ricaviamo che il baricentro G del quadrilatero deve giacere sul
14
segmento G1G2 che unisce i due punti come in figura. Ripetendo il
ragionamento per una suddivisione in triangoli diversa del quadrilatero, si
avrà che G ora dovrà stare sul segmento G 3G 4 . Ne consegue che G si troverà
G2
all’incontro dei due segmenti G1G2 e G 3G 4 .
G
Oggetti scomponibili
Nel caso si debba calcolare il baricentro di una figura piana scomponibile in
elementi dotati di assi di simmetria, si può applicare la proprietà distributiva.
Nell’esempio della lamina a forma di L, si individuano i baricentri dei due
rettangoli che la costituiscono, e che giacciono nei punti G1 e G2 in cui gli assi
G1
G1
G
di simmetria si incontrano. Successivamente si immaginano le masse dei
rettangoli concentrate in questi punti e si individua G lungo la congiungente
G1G2 con la formula per le masse puntiformi. Nel secondo esempio della
G2
lamina a forma di casetta, si opera la scomposizione in un triangolo ed un
rettangolo e si procede analogamente.
Lamine con buchi
Se si ha a che fare con una lamina che presenta un buco, come quella circolare
qui a destra, è possibile seguire la strategia di immaginare un altro buco
simmetrico rispetto al primo e di scomporre l’oggetto in una lamina con due
buchi (e quindi simmetrica rispetto a due assi, con G1 nel loro punto di
G2
G
G1
incontro) ed una lamina più piccola con la forma del buco, in questo caso
anch’essa simmetrica, con G2 nel suo centro. Immaginando poi le masse dei
due elementi concentrate
all’individuazione di G .
nei
loro
baricentri,
si
può
procedere
Esempio 6
Una cassa cubica è appoggiata sopra ad una tavola e sostenuta dai due A
montanti A e B. Calcolare le forze esercitate dai montanti sapendo che:
mCassa 50 Kg , mTavola 5.0 Kg .
Disegniamo lo schema del corpo libero del sistema costituito dalla cassa e della
tavola, considerando che la gravità è applicata nel centro geometrico della
cassa, e nel centro geometrico della tavola, visto che si tratta di oggetti dotati di
assi di simmetria. Le equazioni dell’equilibrio si scrivono:
FA WC WT FB 0
F W W F 0
A
C
T
2.0 m
FA
FB
B
Tutte le forze sono verticali quindi la prima equazione ha solo le componenti
lungo l’asse y :
A
FA mC g mT g FB 0
Per la seconda equazione, dato che è indifferente l’asse rispetto a cui si sceglie
di calcolare i momenti, prendiamo quello che buca il piano del foglio passando
per A. In questo modo infatti i calcoli sono facilitati perché il momento di FA ,
incognita,
B
1.4 m
risulta nullo dato che la sua retta di azione passa per l’asse.
15
G
G
1.4 m
WC
B
2.0 m
WT
Considerato che i pesi della cassa e della tavola tendono a far ruotare il sistema
in verso orario attorno all’asse per A (e quindi hanno momenti negativi) e che
inoltre il braccio di WT misura la metà della lunghezza totale della tavola
stessa, si ha:
braccio di FA nullo: momento nullo
braccio di WC pari a 1.4 m , provoca rotazione oraria: momento negativo
braccio di WT pari a 1.7 m , provoca rotazione oraria: momento negativo
braccio di FB pari a 3.4 m , provoca rotazione antioraria: momento positivo
da cui sostituendo:
0 1.4 mC g 1.7 mT g 3.4 FB 0
Dall’equazione dei momenti si ricava agevolmente:
1.7 mT g 1.4 mC g
(1.7 5.0 1.4 50) 9.8
FB
226 N
3.4
3.4
ed inserendo il risultato nell’equazione delle forze:
FB mC g mT g FA 50 9.8 5.0 9.8 226 313 N
E’ utile risolvere nuovamente il problema scegliendo un differente asse per i
momenti, ad esempio passante il punto B oppure per il baricentro della tavola
16