Equazioni e disequazioni goniometriche

1
ARCHI ASSOCIATI
Si tratta di angoli in cui le funzioni goniometriche mantengono lo stesso valore
assoluto, cambiando al più il segno. Per questo motivo, le tavole goniometriche
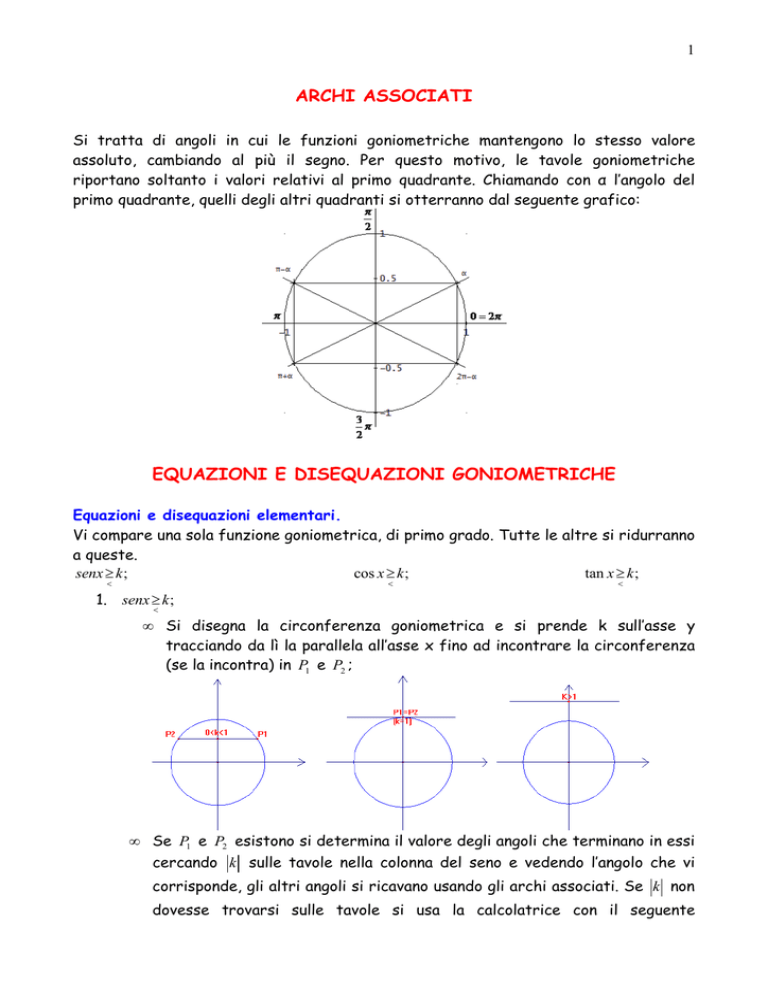
riportano soltanto i valori relativi al primo quadrante. Chiamando con α l’angolo del
primo quadrante, quelli degli altri quadranti si otterranno dal seguente grafico:
EQUAZIONI E DISEQUAZIONI GONIOMETRICHE
Equazioni e disequazioni elementari.
Vi compare una sola funzione goniometrica, di primo grado. Tutte le altre si ridurranno
a queste.
senx ≥ k ;
cos x ≥ k ;
tan x ≥ k ;
<
<
<
1. senx ≥ k ;
<
•
•
Si disegna la circonferenza goniometrica e si prende k sull’asse y
tracciando da lì la parallela all’asse x fino ad incontrare la circonferenza
(se la incontra) in P1 e P2 ;
Se P1 e P2 esistono si determina il valore degli angoli che terminano in essi
cercando k sulle tavole nella colonna del seno e vedendo l’angolo che vi
corrisponde, gli altri angoli si ricavano usando gli archi associati. Se k non
dovesse trovarsi sulle tavole si usa la calcolatrice con il seguente
2
procedimento: passare in radianti e poi digitare sin −1 k usare poi sempre gli
•
•
•
archi associati;
Le linee tracciate dividono la circonferenza in due archi, quello superiore e
quello inferiore sceglieremo l’arco superiore se il verso della disequazione
è> e quello inferiore se è <.
La soluzione è data sempre da uno o più intervalli compresi tra due estremi,
ricorda di scegliere gli archi giusti ruotando in senso antiorario da 0 a 2π
1− 5
1− 5
≈ −0.3 la corda sarà sotto l’asse x.
Es. senx >
Poiché
4
4
−1+ 5
cioè il valore positivo
Cerchiamo sulle tavole nella colonna del seno
4
corrispondente e troviamo che esso corrisponde all’ angolo
π
10
, poiché ci
troviamo nel terzo e quarto quadrante gli angoli cercati saranno π +
2π −
π
10
.
Sol: 0 ≤ x < π +
Scriviamo
π
10
∨ 2π −
π
10
la
soluzione
partendo
da
π
10
e
0
< x ≤ 2π
2. cos x ≥ k ;
<
•
Si disegna la circonferenza goniometrica e si prende k sull’asse x tracciando da
lì la parallela all’asse y fino ad incontrare la circonferenza (se la incontra) in P1
e P2 ;
3
•
Se P1 e P2 esistono si determina il valore degli angoli che terminano in essi
cercando k sulle tavole nella colonna del coseno e vedendo l’angolo che vi
corrisponde, gli altri angoli si ricavano usando gli archi associati. Se k non
dovesse trovarsi sulle tavole si usa la calcolatrice con il seguente
procedimento: passare in radianti e poi digitare cos −1 k usare poi sempre
•
•
•
gli archi associati;
Le linee tracciate dividono la circonferenza in due archi, quello di destra e
quello di sinistra, sceglieremo l’arco di destra se il verso della disequazione
è> e quello di sinistra se è <.
La soluzione è data sempre da uno o più intervalli compresi tra due estremi,
ricorda di scegliere gli archi giusti ruotando in senso antiorario da 0 a 2π.
2− 6
2− 6
Es. cos x <
Poiché
≈ −0.26 la corda sarà a sinistra dell’asse
4
4
6− 2
y. Cerchiamo sulle tavole nella colonna del coseno
cioè il valore
4
5
positivo corrispondente e troviamo che esso corrisponde all’ angolo
π,
12
poiché ci troviamo nel secondo e terzo quadrante gli angoli cercati saranno
5
5
π− π
e
π + π . Scriviamo la soluzione partendo da 0
12
12
5
5
Sol: π − π < x < π + π
12
12
4
3. tan x ≥ k ;
<
•
Si disegna la circonferenza goniometrica e la retta ad essa tangente
nell’intersezione con il semiasse x positivo, si prende poi k sulla tangente e si
traccia da k la retta passante per il centro della circonferenza, P1 e P2 sono i
punti di intersezione della retta con la circonferenza;
• Si determina il valore degli angoli che terminano in P1 e P2 cercando k sulle
tavole nella colonna della tangente e vedendo l’angolo che vi corrisponde, gli
altri angoli si ricavano usando gli archi associati. Se k non dovesse trovarsi
sulle tavole si usa la calcolatrice con il seguente procedimento: passare in
radianti e poi digitare tan −1 k usare poi sempre gli archi associati;
•
•
Poiché il periodo della tangente è π, bisogna considerare solo la
semicirconferenza a destra dell’asse y, prendendo l’arco superiore se il verso
della disequazione è > e quello inferiore se è <. L’altra semicirconferenza si
completa per simmetria
Es. tan x < 2 − 1 . Poiché 2 − 1 ≈ 0.4 , P1 e P2 si trovano nel primo e terzo
quadrante e valgono
π
e π+
π
; essendo il verso della disequazione < prendo
8
8
l’arco verso il basso, poi faccio la simmetria
Scrivo infine la soluzione Sol. 0 ≤ x <
π
8
∨
π
2
< x <π +
π
3
∨ π < x ≤ 2π
8 2
5
Equazioni e disequazioni elementari in cui l’argomento è diverso da x.
Si tratta di disequazioni del tipo sen(ax + b ) ≥ k ; o con le altre funzioni
<
goniometriche. Si risolvono come quelle elementari tranne al momento in cui si
3
scrive la soluzione finale. Se per esempio la soluzione dovesse essere π < x < 2π
2
3
nel nostro caso diventerebbe π < ax + b < 2π a questo punto occorre isolare la x
2
3
π −b
2π − b
2
portando b sia a sinistra che a destra e poi dividere per a,
<x<
come
a
a
si può vedere la soluzione non chiude più la circonferenza al primo giro perché non
arriva più a 2π, in questo caso occorre prendere le soluzioni su tanti giri quanto
vale a.
1
π
π
Es. cos(2 x ) ≤ . Procedendo come indicato sopra si ottiene
≤ 2 x ≤ 2π −
ma
2
3
3
π
anche aggiungendo un secondo giro (perché a vale 2)
dividiamo ora ogni termine per 2. Soluzione:
π
6
≤ x ≤π −
π
6
3
∨
π
6
+ 2π ≤ 2 x ≤ 2π −
+π ≤ x ≤π −
π
6
π
3
+ 2π
+π .
Equazioni e disequazioni di secondo grado
Si tratta di equazioni e disequazioni in una sola funzione goniometrica:
asen 2 x + bsenx + c ≥ 0; a cos 2 x + b cos x + c ≥ 0; a tan 2 x + b tan x + c ≥ 0
<
<
<
*Potrebbe succedere che nella stessa disequazione compaiano sia sen 2 x che cos 2 x ,
in questo caso basta trasformare una nell’altra usando la prima relazione
sen 2 x = 1 − cos 2 x
2
2
fondamentale della goniometria sen x + cos x = 1 ⇒
*
cos 2 x = 1 − sen 2 x
Dopo aver sostituito la funzione goniometrica con t si risolve la disequazione
at 2 + bt + c ≥ 0 e poi si riportano gli archi sulla circonferenza nel seguente modo:
<
senx
6
cosx
tanx
Ricorda poi di fare la simmetria.
Equazioni e disequazioni lineari.
Si presentano nella forma asenx + b cos x + c ≥ 0 .
<
Si risolvono usando le formule parametriche che le trasformano in disequazioni di
secondo grado nella variabile t, dopo si procede come nel caso precedente l’unica
x
differenza è che t = tan per cui la soluzione prevederà intervalli in cui la variabile
2
x
è , occorrerà quindi moltiplicare tutto per 2.
2
Es.
 2t

2
1+ t
senx + 5 cos x > 3 2 .
Con
le
formula
2
2
2t + 5 − 5t − 3 2 − 3 2t 2
 1− t 


+
5
>
3
2
⇒
> 0,
 
2 
1+ t2
 1+ t 
parametriche
essendo
il
si
avrà
denominatore
sicuramente positivo, può essere tolto, sommando i termini simili si arriva a:
17 − 13 2
− 5t 2 − 3 2t 2 + 2t + 5 − 3 2 > 0 che risolta ci darà
< t < 2 − 1 cioè
b
7
a
c
17 − 13 2
x
< tan < 2 − 1 che risolta sulla circonferenza
7
2
7
π
x π
x
< ∨ π − tan −1 (0.2 ) < < π + < 2π − tan −1 (0.2 ) < x ≤ 2π
2 8
2
8
Dobbiamo ora moltiplicare ogni termine per 2 in modo da determinare i valori
relativi ad x, come si può vedere si supera il primo giro di circonferenza, basta
quindi nel scrivere la soluzione fermarsi al primo mezzo giro
π
x π
x
0 ≤ < ∨ π − tan −1 (0.2 ) < < π ⇒ 0 ≤ x < ∨ 2π − 2 tan −1 (0.2 ) < x < 2π
2 8
2
4
0≤
Equazioni e disequazioni che presentano più argomenti diversi.
Si risolvono con le formule goniometriche.
Disequazioni goniometriche in forma di frazioni o prodotti.
Si risolvono con lo schema con i segni come le disequazioni algebriche, solo che lo
schema si fa sulla circonferenza.
NUM 2senx − 1 > 0 senx > 1
2 senx − 1
Es.
< 0;
⇒
2 si passa ora alla circonferenza
DEN
cos x > 0
cos x
cos x > 0
Sol. 0 < x <
π
6
∨
π
2
< x <π −
π
3
∨ π < x < 2π
6 2
8
Esercizi.
1. senx>2;
2. cosx>-2;
3. tanx>-1;
4. 2senx-1<0;
5. 2 cos x < 0;
6.
3 tan x − 1 > 0;
2 cos(3 x ) < 3 ;
x
8.
2 sen + 1 > 0;
2
π

9. tan  x +  > 3;
4

2
10. 2 cos x < 1;
7.
11. 2 sen 2 x − senx ≥ 0;
senx
12.
≤ 0;
cos x + 1
13. 2 cos 2 x + 3 cos x + 1 < 0;
14. sen(2x)-cosx<0;
15. 2 sen 2 x < 3 cos x;
16. 5sen 2 x + senx + cos 2 x >
5
;
2
17. tan 2 x + 2 tan x < 3;
18. sen2x+cos2x<1;
x
19. senx − cos > 0;
2
2
20. 2 3 cos x − sen 2 x < 3;
3senx + cos x ≥ 1;
x
22. sen 2 + cos x + 1 > 0;
2
2 cos x − 3
23.
≥ 0;
senx
24. cos x − 3senx < 0.
21.