Appunti delle lezioni svolte in classe
Equazioni goniometriche
Si dice goniometrica un’equazione in cui l’incognita compare come argomento di una o più funzioni
goniometriche.
Equazioni elementari
sen x = a
cos x = b
sen x = a
tg x = c
cos x = b
tg x = c
1 a 1 ammette soluzioni
1 b 1 ammette soluzioni
Poiché il seno di un angolo
rappresenta l’ordinata del punto
della circonferenza goniometrica a
cui l’angolo è associato, dobbiamo
trovare i punti della circonferenza
goniometrica di ordinata a.
Poiché il coseno di un angolo
rappresenta l’ascissa del punto della
circonferenza goniometrica a cui
l’angolo è associato, dobbiamo
trovare i punti della circonferenza
goniometrica di ascissa b.
Gli angoli che hanno uguale seno,
associati a B1 e B2 , sono angoli
supplementari e perciò, detta
l’ampiezza di uno di essi, le
soluzioni sono:
Gli angoli che hanno uguale coseno, Gli angoli che hanno uguale
associati a B1 e B2 , sono angoli tangente, associati a P e
opposti e perciò, detta l’ampiezza Q , sono angoli che
differiscono per 180° e
di uno di essi, le soluzioni sono:
perciò, detta l’ampiezza
di uno di essi, le soluzioni
sono:
x k 360 e
x k180
x k 360 e
x 180 k360
x 2k e
x 2k
x k 360
x 2k e
x 2k e
ammette soluzioni
qualunque sia c
Sulla tangente geometrica
condotta nel punto E si
prende il punto T di
ordinata c; la retta del
diametro passante per T
incontra la circonferenza nei
punti P e Q.
x k
Percorrendo
la
circonferenza goniometrica,
troviamo:
,
generale:
C. Ferone
1
e
in
Appunti delle lezioni svolte in classe
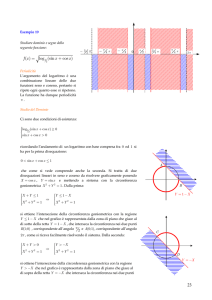
Esempi:
1. Risolvere : senx
1
.
2
1
, si osserva che i punti di intersezione di questa
2
7
7
con la circonferenza sono estremi degli archi di misura e . Quindi le soluzioni sono:
6
6
6
Disegnate la circonferenza goniometrica e la retta Y
7
x 2k e x 2k .
6
6
2. Risolvere : senx
2
.
3
2
2k e
3
L’equazione è soddisfatta dagli infiniti angoli espressi dalle formule: x arcsen
2
x arcsen 2k .
3
3. Risolvere : sen 2 x
Essendo sen
x
4
2
.
2
2
3
, ne segue che 2 x 2k e 2 x 2k 2k da cui:
4
4
4
2
3
k e x k .
8
8
4. Risolvere : sen 2 x senx 2 0 .
Essendo questa un’equazione algebrica di secondo grado in senx , le radici si ottengono dalla formula
risolvente di una equazione di secondo grado e dà come soluzioni: senx 2 e senx 1 . La prima è
impossibile, mentre la seconda ha soluzioni: x
2
2k .
5. Risolvere : sen2x 30 cosx 30 .
Per la relazione tra seno e coseno di angoli complementari, si ha:
cosx 30 sen90 2x 30 sen(60 x)
L’equazione diventa: sen2x 30 sen60 x . Avremo allora:
2x 30 60 x k 360 x 30 k120 e
2x 30 180 60 x k 360 x 150 k 360
C. Ferone
2
Appunti delle lezioni svolte in classe
2
.
2
6. Risolvere : cos x
Disegnate la circonferenza goniometrica e la retta X
2
, si osserva che i punti di intersezione di questa
2
con la circonferenza sono estremi degli archi di misura: x
4
2k e x
4
2k .
1
4
7. Risolvere : cos x .
1
2k e
4
L’equazione è soddisfatta dagli infiniti angoli espressi dalle formule: x arccos
1
x arcsen 2k .
4
8. Risolvere : cos
2
3
Essendo cos
x
1
.
2
2
1
x 2
x
2
, ne segue che 2k e 2k da cui:
2
2 3
2
3
4
4
x 4k e x 4k .
3
3
9. Risolvere : cos2x 30 cos x .
Affinché due angoli abbiano lo stesso coseno, è necessario e sufficiente che differiscano di un numero
intero di angoli giri o che l’uno differisca per un numero intero di angoli giri dell’opposto dell’altro, quindi:
2x 30 x k 360 x 30 k 360 e 2x 30 x k 360 x 10 k120 .
10. Risolvere :
2senx cos x cos x 0 .
Raccogliendo cos x a fattor comune si ottiene: cos x
elementari: cos x 0 e
2 senx 1 0 da cui si ricavano le equazioni
2 cos x 1 0 .
La prima ammette le soluzioni: x
C. Ferone
5
7
k , la seconda le soluzioni: x 2k e x 2k .
2
4
4
3