Primo teorema di euclide
Enunciato con l'equivalenza
In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo avente per
dimensioni l'ipotenusa e la proiezione di quel cateto sull'ipotenusa stessa.
Dimostrazione
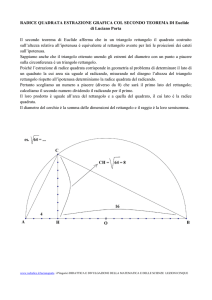
Facendo riferimento alla figura, si consideri il triangolo rettangolo
ABC. Sul cateto BC si costruisca il quadrato BDEC e sia CH la
proiezione del cateto BC sull'ipotenusa CA. Si costruisca il
rettangolo HCLM avente CL congruente a CA. Si prolunghi il lato ED
dalla parte di D fino ad incontrare in F la retta contenente il
segmento CL e in G la retta contenente il segmento MH. Si vuole
dimostrare che il quadrato BDEC è equivalente al rettangolo
HCLM.
Si considerino ora i triangoli ABC e CFE. Essi hanno:
BC congruente a CE per costruzione,
l'angolo ABC congruente all'angolo FEC perché retti,
l'angolo BCA congruente all'angolo ECF perché entrambi
complementari dello stesso angolo FCB.
Dunque, per il secondo criterio di congruenza dei triangoli, i
triangoli ABC e CFE sono congruenti, e in particolare si ha
che CA è congruente a CF.
Si considerino il quadrato BDEC e il parallelogramma FCBG. Essi hanno la stessa base CB e la
stessa altezza DB (perché DE e GF appartengono alla stessa retta) e quindi sono equivalenti.
Si considerino il parallelogramma FCBG e il rettangolo HCLM. Essi hanno basi congruenti (infatti
FC è congruente a CA per dimostrazione precedente, e CA è congruente a CL per costruzione,
quindi FC è congruente a CL per la proprietà transitiva della congruenza) e la stessa altezza (infatti
FC e CL appartengono alla stessa retta, e così pure BG e MH), quindi sono equivalenti. Q.
Allora, per la proprietà transitiva dell'equivalenza, il quadrato BDEC è equivalente al rettangolo
HCLM.
Secondo teorema di Euclide
Enunciato con l'equivalenza
In un triangolo rettangolo, il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al
rettangolo avente per dimensioni le proiezioni dei cateti sull'ipotenusa.
Dimostrazione
Dimostrazione del secondo teorema di Euclide
mediante l'equivalenza
Facendo riferimento alla figura, sia CL congruente
e perpendicolare a CA e CR congruente a CH.
Si vuole dimostrare che il quadrato HPQB è
equivalente al rettangolo RLMS.
Si consideri il triangolo rettangolo BCH e ad esso
si applichi il teorema di Pitagora. Si ottiene che il
quadrato CBDE è equivalente alla somma dei
quadrati HPQB e CRSH.
Si consideri ora il triangolo rettangolo ABC, e ad
esso si applichi il primo teorema di Euclide. Si
ottiene che il quadrato CBDE è equivalente al
rettangolo CLMH, ma tale rettangolo può essere
considerato come la somma del quadrato CRSH e
del rettangolo RLMS.
Allora la somma di HPQB e CRSH è equivalente alla somma di CRSH e RLMS, quindi, per
differenza, HPQB è equivalente a RLMS.
C.V.D.
Teorema di Pitagora
Enunciato
In ogni triangolo rettangolo, l'area del quadrato costruito sull'ipotenusa è equivalente alla somma
delle aree dei quadrati costruiti sui cateti.
Dimostrazioni
La dimostrazione classica del teorema di Pitagora completa il primo libro degli Elementi di Euclide,
e ne costituisce il filo conduttore. Dato che richiede il postulato delle parallele, esso non vale nelle
geometrie non-euclidee e nella geometria neutrale. Nel testo di Euclide la dimostrazione del
teorema è immediatamente preceduta dalla dimostrazione della costruibilità dei quadrati.
L'esistenza stessa dei quadrati dipende infatti dal postulato delle parallele e viene meno nelle
geometrie non euclidee. Questo aspetto del problema è in genere trascurato nella didattica
contemporanea, che tende spesso ad assumere come ovvia l'esistenza dei quadrati.
La dimostrazione del teorema di Pitagora consiste nel riempire uno stesso quadrato di lato uguale
alla somma dei cateti prima con quattro copie del triangolo rettangolo più il quadrato costruito
sull'ipotenusa e poi con quattro copie del triangolo rettangolo più i quadrati costruiti sui cateti, come
in figura