1° teorema di Euclide
Definizione e dimostrazione del
primo teorema di Euclide
LAVECCHIA FRANCESCO
II G
A.S.: 2011/2012
I triangoli rettangoli sono triangoli
particolari che hanno delle proprietà in
più rispetto agli altri triangoli; fra
queste rivestono particolare
importanza quelle enunciate dai
teoremi di Euclide e di Pitagora.
Il PRIMO TEOREMA DI EUCLIDE afferma che:
In ogni triangolo rettangolo il quadrato costruito su un cateto è equivalente al
rettangolo che ha per lati l’ipotenusa e la proiezione di quel cateto sull’ipotenusa.
Dimostreremo che il
quadrato verde costruito
sul cateto minore sarà
uguale al rettangolo verde
appartenente al quadrato
costruito sull’ipotenusa e
avente come lati il cateto
citato e l’ipotenusa stessa.
La stessa cosa vale per il
quadrato e il rettangolo
rosa.
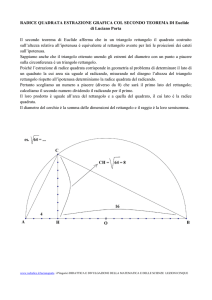
Possiamo renderci conto del significato di questo
teorema osservando la figura; in essa:
• il triangolo ABC è rettangolo in B
• Il quadrato giallo è costruito sul cateto BC.
Per ottenere il rettangolo giallo che ha per lati
l’ipotenusa e la proiezione di BC sull’ipotenusa,
facciamo questa costruzione:
• dal vertice C tracciamo la perpendicolare
all’ipotenusa AC e prendiamo su di essa il
segmento CL ≅ AC
• tracciamo dal vertice B dell’angolo retto la
perpendicolare a AC: il segmento CH è la
proiezione di BC sull’ipotenusa
• costruiamo adesso il rettangolo che ha per lati
CL e CH.
Il teorema afferma che il quadrato giallo è
equivalente al rettangolo giallo; veniamo adesso
alla dimostrazione del teorema.
DIMOSTRAZIONE
La dimostrazione è abbastanza semplice se
consideriamo il parallelogramma ausiliario FGBC che
otteniamo prolungando il lato superiore ED del
quadrato e le due rette dei lati CL e HM del rettangolo.
Osserviamo prima di tutto il triangolo ABC e il
triangolo CED che si è venuto in questo modo a
formare sono congruenti (CB≅CE, l’angolo ACB≅ECF
perché complementari dello stesso angolo BCF); di
conseguenza, essendo CF≅AC, anche CF≅CL.
Per i teoremi sull’equivalenza che abbiamo studiato
nel precedente paragrafo abbiamo che:
• il quadrato CEDB è equivalente al parallelogramma
FCBG (hanno la stessa base BC e la stessa altezza BD)
• il parallelogramma FCBG è equivalente al rettangolo
CHML (hanno rispettivamente come basi CF e CL che
sono segmenti congruenti, e la stessa altezza CH).
Dunque, per la proprietà transitiva:
- ECBD è equivalente a CBGF che è equivalente a
CHML, allora ECBD è equivalente a CHML.
FINE