PRIMO TEOREMA DI EUCLIDE
Enunciato con l'equivalenza
In un qualsiasi triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo
avente per dimensioni l'ipotenusa stessa e la proiezione di quel cateto sull'ipotenusa.
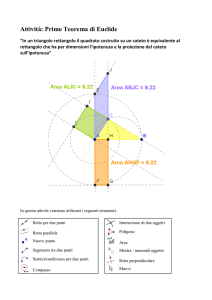
Ip: Sia ABC un triangolo rettangolo in B.
Th: BC2 = AC∙HC
oppure
BA2 = AC∙AH
Dimostrazione
Facendo riferimento alla figura, si consideri il triangolo rettangolo
. Sul cateto
si
costruisca il quadrato
e sia
la proiezione del cateto
sull'ipotenusa
. Si
costruisca il rettangolo
avente
congruente a
. Si prolunghi il lato
dalla
parte di
fino ad incontrare in
la retta contenente il segmento
e in la retta contenente il
segmento
. Si vuole dimostrare che il quadrato
è equivalente al rettangolo
.
Si considerino ora i triangoli
e
. Essi hanno:
congruente a
per costruzione,
l'angolo
congruente all'angolo
l'angolo
congruente all'angolo
angolo
.
perché retti,
perché entrambi complementari dello stesso
Dunque, per il secondo criterio di congruenza dei triangoli, i triangoli
congruenti, e in particolare si ha che
è congruente a
.
e
sono
Si considerino il quadrato
la stessa altezza
(perché
e
e il parallelogramma
. Essi hanno la stessa base
e
appartengono alla stessa retta) e quindi sono equivalenti.
Si considerino il parallelogramma
e il rettangolo
. Essi hanno basi congruenti
(infatti
è congruente a
per dimostrazione precedente, e
è congruente a
per
costruzione, quindi
è congruente a
per la proprietà transitiva della congruenza) e la stessa
altezza (infatti
e
appartengono alla stessa retta, e così pure
e
), quindi sono
equivalenti.
Allora, per la proprietà transitiva dell'equivalenza, il quadrato
.
c.v.d.
è equivalente al rettangolo