www.appuntiscuolasuperiore.altervista.org
FUNZIONI GONIOMETRICHE INVERSE
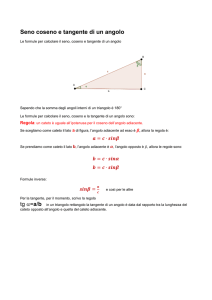
Vengono assegnate le seguenti funzioni goniometriche:
sen (x) = a
cos (x) = b
tg (x) = c
cotg (x) = d
Dove ovviamente i valori di a e di b sono compresi tra 1 e -1.
Ci si chiede se, conoscendo i valori di a, b, c e d è possibile sapere quali angoli hanno
seno, coseno, tangente e cotangente pari a questi valori.
In altre parole, se in precedenza, noto l’angolo si sono ricavati i valori di seno, coseno,
tangente e cotangente corrispondenti, adesso vogliamo fare esattamente il contrario.
x
x
x
x
=
=
=
=
arc
arc
arc
arc
sen (a)
cos (b)
tg (c)
cotg (d)
Le funzioni goniometriche sono tali per cui, attribuito un preciso valore all’angolo, ne
risulta un unico e preciso valore di seno, coseno, tangente e cotangente. Esiste dunque
un rapporto univoco tra angolo e funzione goniometrica.
Non è invece la stessa cosa per le funzioni goniometriche inverse, nelle quali, ad un
preciso valore dell’arco seno, arco coseno, arco tangente o arco cotangente esistono
infiniti valori degli angoli che soddisfano l’equazione. Le funzioni goniometriche inverse si
dicono dunque “infinitivoche”.
Tuttavia queste funzioni possono “diventare” univoche anch’esse a seconda di quale sia
l’intervallo di osservazione considerato. Vediamo qualche esempio.
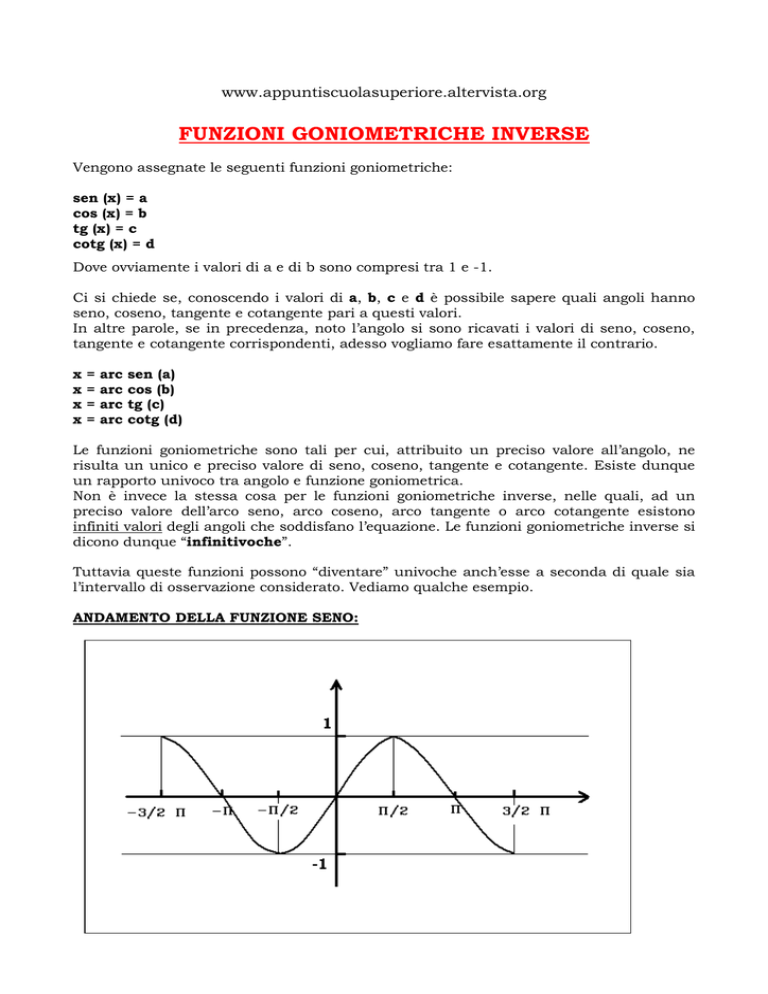
ANDAMENTO DELLA FUNZIONE SENO:
Nell’intervallo tra 0 e π, come è possibile vedere dal grafico, ci sono già due valori di
angoli che hanno lo stesso seno.
Considerando invece l’intervallo tra –π/2 e π/2, notiamo che al suo interno per ogni
valore del seno corrisponde un unico valore di angolo.
ESEMPIO:
arc sen (y) = 1 → y = π/2
Abbiamo trovato l’unico angolo –all’interno dell’intervallo considerato- che abbia un seno
pari ad 1.
arc sen (y) = x
y è un angolo il cui seno è pari ad x → x = sen (y)
x non può andare oltre 1 e -1, mentre y non può andare –se vogliamo un unico valoreoltre –π/2 e π/2.
E’ ovvio che si sarebbero potuti considerare altri intervalli ugualmente “univoci”.
ANDAMENTO DELLA FUNZIONE ARC SENO:
Come si nota, il grafico è inverso a quello del seno, con ascisse ed ordinate in posizione
inversa.
ANDAMENTO DELLA FUNZIONE COSENO:
Stavolta, come è possibile vedere dal grafico, è necessario scegliere nell’intervallo tra 0 e
π, per ottenere una corrispondenza tra angoli e funzione goniometrica inversa.
Anche in questo caso è ovvio che si sarebbero potuti considerare altri intervalli
ugualmente “univoci”.
ESEMPIO:
arc cos (y) = x
y è un angolo il cui coseno è pari ad x → x = cos (y)
x non può andare oltre 1 e -1, mentre y non può andare –se vogliamo determinare un
unico valore- oltre 0 e π.
ANDAMENTO DELLA FUNZIONE ARC COSENO:
Come si nota, il grafico è inverso a quello del coseno, con ascisse ed ordinate in posizione
inversa.
ARC TANGENTE E ARC COTANGENTE:
Brevemente, diremo che per la funzione arc tangente occorre considerare lo stessp
intervallo dell’ arc seno (–π/2 e π/2) e per la funzione arc cotangente lo stesso intervallo
dell’arc coseno (0 e π).
Anche in questo vaso funzioni goniometriche e rispettive funzioni goniometriche inverse
hanno grafici identici, ma invertiti.
ESEMPIO:
arc tan (y) = x
y è un angolo la cui tangente è pari ad x → x = tan (y)
y non può andare –se vogliamo un unico valore- oltre l’intervallo –π/2 e π/2, purchè non
sia pari ad uno di questi due valori (altrimenti la tangente non è definitiva).
arc cotg (y) = x
y è un angolo la cui cotangente è pari ad x → x = cotg (y)
y non può andare –se vogliamo un unico valore- oltre l’intervallo 0 e π, purchè non sia
pari ad uno di questi due valori (altrimenti la cotangente non è definitiva).