Compito 1
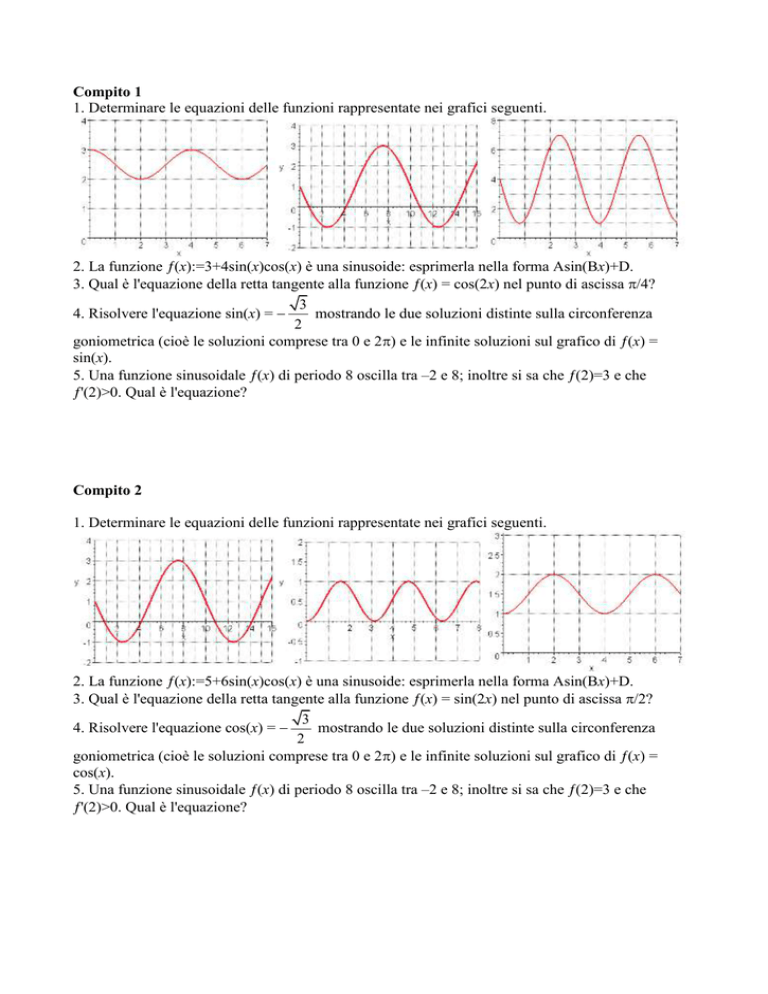
1. Determinare le equazioni delle funzioni rappresentate nei grafici seguenti.
2. La funzione (x):=3+4sin(x)cos(x) è una sinusoide: esprimerla nella forma Asin(Bx)+D.
3. Qual è l'equazione della retta tangente alla funzione (x) = cos(2x) nel punto di ascissa /4?
3
4. Risolvere l'equazione sin(x) =
mostrando le due soluzioni distinte sulla circonferenza
2
goniometrica (cioè le soluzioni comprese tra 0 e 2) e le infinite soluzioni sul grafico di (x) =
sin(x).
5. Una funzione sinusoidale (x) di periodo 8 oscilla tra –2 e 8; inoltre si sa che (2)=3 e che
'(2)>0. Qual è l'equazione?
Compito 2
1. Determinare le equazioni delle funzioni rappresentate nei grafici seguenti.
2. La funzione (x):=5+6sin(x)cos(x) è una sinusoide: esprimerla nella forma Asin(Bx)+D.
3. Qual è l'equazione della retta tangente alla funzione (x) = sin(2x) nel punto di ascissa /2?
3
4. Risolvere l'equazione cos(x) =
mostrando le due soluzioni distinte sulla circonferenza
2
goniometrica (cioè le soluzioni comprese tra 0 e 2) e le infinite soluzioni sul grafico di (x) =
cos(x).
5. Una funzione sinusoidale (x) di periodo 8 oscilla tra –2 e 8; inoltre si sa che (2)=3 e che
'(2)>0. Qual è l'equazione?
Compito 3
1. Considera, nell'intervallo di tempo [0, 2], il moto piano caratterizzato dalle equazioni
parametriche
x t sin t
y 1 cos t
dove t è misurato in secondi, x e y in metri.
a) Tracciare la traiettoria del moto, analizzando dove si trova il punto agli istanti t = 0, /2, , 3/2,
2 secondi.
b) Qual è il vettore velocità in ciascuno di quegli istanti? Qual è il modulo della velocità in ciascuno
di quegli istanti?
c) Determinare in quale istante la velocità è 1.5 m/s.
d) Determinare in quale istante la direzione del moto è di 60°.
2. Il punto A si muove di moto armonico sull'asse x tra 2 e 2, con periodo 4 s; la sua posizione
iniziale è in (2,0). Il punto B si muove di moto circolare uniforme sulla circonferenza di centro O e
raggio 1 con velocità angolare ; la sua posizione iniziale è (1,0).
a) Scrivere le equazioni parametriche del moto del punto A e del punto B.
b) Determinare in modo tale che i due punti si scontrino nel punto (1, 0) quando A vi transita per
la prima volta.
3. Scrivere la funzione (x) = sin(x)cos(x) nella forma (x)=Asin(x+B) e risolvere la disequazione
(x) > 1.
Compito 4
1. Considera, nell'intervallo di tempo [0, ], il moto piano caratterizzato dalle equazioni
parametriche
x cos 2t
t
y sin 2
dove t è misurato in secondi, x e y in metri.
a) Descrivere la traiettoria del moto e tracciarla sul foglio, precisando in quali istanti attraversa
l'asse y.
b) Descrivere come varia la velocità: tracciare un grafico velocità-tempo del moto nell'intervallo di
tempo [0,], precisando in quali istanti la velocità è minima o massima.
c) Determinare componenti del vettore velocità, modulo della velocità e direzione della velocità
negli istanti t1 = 0, t2 = /4 s, t3 = s.
2. La funzione (x) = sin(x) + 3 cos(x) è una sinusoide. Perché? Qual è l'ampiezza? Quali sono le
soluzioni della disequazione (x) > 3 ?
Compito 5
PROVA STRUTTURATA
1) Completa le seguenti definizioni:
a) Si definisce grado sessagesimale la ............................ dell’angolo giro
b) La misura di un angolo al centro di una circonferenza in radianti è il rapporto tra la misura
dell’ ............ corrispondente e la misura del ............... della circonferenza
c) Un angolo giro misura ................ radianti
2) Associa alle misure di angoli della prima colonna la corrispondente unità di misura
riportata nella seconda colonna
a)
b)
c)
d)
3)
(30,75)°
30° 25’
2
27’’
a)
b)
c)
d)
b) 2
d)
3
radianti?
2
b) 57
d)
Qual è la misura in gradi dell’angolo che misura
a) 1
c) 90
5)
grado sessagesimale
grado decimale
secondo
radiante
Qual è la misura in radianti dell’angolo la cui misura in gradi è 60?
a) 6
c)
6
4)
A)
B)
C)
D)
Dato il triangolo in figura, come è definito cos?
A
B
a)
c)
6)
b)
d)
AB
BC
BC
AC
Quali delle seguenti uguaglianze è verificata per qualsiasi angolo acuto?
a)
b)
c)
d)
7)
AB
AC
BC
AB
C
sen2 + cos2 1 = 0
sen2 = 1 + cos2
cos2 = sen2 + 1
sen2 = 1 + cos2
Se di un triangolo, rettangolo in , conosci il cateto b e l’angolo ad esso opposto quali,
tra le seguenti relazioni, puoi utilizzare per trovare l’altro cateto c e l’ipotenusa a?
a)
c)
b
sen a
b
tg
c
90
b
tg
c
b)
sen
cos
d)
cos
b
a
b
a
90
b
a
8) Associa ad ogni elemento della prima colonna il corrispondente valore tra quelli elencati
nella seconda colonna
a) cos 30°
A)
a)
3
b) tg 45°
B)
b)
1
2
c)
C)
c)
3
sen
6
2
d)
D)
d)
2
tg
3
2
e)
E)
e)
3
cos
3
3
f) sen 60°
F)
1
f)
Scegli in modo da completare la frase correttamente
9) Per risolvere un triangolo qualunque occorre conoscere
a) il seno di due angoli
b) il seno e il coseno di due angoli
c) tre angoli
d) tre elementi di cui almeno un lato
10) Il teorema del coseno si può applicare a un triangolo rettangolo?
a) No
b) No, perché quando l’angolo compreso è retto il suo seno vale 0 e allora si ottiene il
teorema di Pitagora
c) Sì, purché l’angolo compreso non sia retto
d) Sì, perché il teorema del coseno vale per un triangolo qualsiasi e quindi anche per il
triangolo rettangolo
Compito 6
1. cos4x - 3cos2xsen2x =0
sen (2 x) tgx
2.
=0
cot g 2 x 3
3. sen( x ) cos( x ) 0
3
6
4. sen(3x-3) = cos(x+3)
5. 4sen(x/2) - 2 3 cos(x/2) +1=0
6. Considera la disequazione
x + 2 senx 0 Come potresti ottenere informazioni sulle sue soluzioni?
Compito 7
1. sen4x - 2cos2xsen2x =0
sen(2 x) tgx
2.
=0
(cot g (2 x) 3) 2
3. cos( x ) sen( x ) 0
3
6
4. cos(3-5x) = sen(2x+1)
5. 4sen(2x) - 2 3 cos(2x) +1=0
6. Considera la disequazione
x + 2 cosx 0 Come potresti ottenere informazioni sulle sue soluzioni?
Compito 8
1.
Dato il trapezio isoscele ABCD avente AB = 40, CD= 10 tg(ABC) = 4/3, determinare
a) perimetro e area del trapezio
b) dimostrare che ABCD è circoscrittibile a una circonferenza
c) i raggi delle circonferenze circoscritta e inscritta
2.
3.
Sia AC = r 3 una corda di una semicirconferenza di diametro AB = 2r. Determinare
sull'arco AC un punto P tale che risulti AP+PC = 2r
Nella semicirconferenza di diametro AB = 2r è inscritto il triangolo rettangolo isoscele
ABC. Determinare sull'arco AC un punto P in modo che sia massima la somma AP+PB+PC
Punteggio, indicativo: 1a) 2 punti
1b) 1 punto
1c) 2 punti
2) 2 punti
3) 3 punti
Compito 9.
e l’altezza
6
AH relativa al lato BC di misura h. Si conducano per H due rette fra loro perpendicolari in modo
che, dette P l’intersezione di una di esse con il cateto AB e Q l’intersezione dell’altra con il cateto
PB
AC, il segmento PQ sia tale che PQ2 = 4 3 AP
. Determinare l’ampiezza dell’angolo acuto
3 2
che una di tali rette forma con la retta BC.
Si consideri il triangolo rettangolo ABC, retto in A e avente l’angolo in B di misura
Compito 10.
Data la semicirconferenza di centro O e raggio r, si consideri il triangolo isoscele ABV i cui lati
obliqui AV e BV siano tangenti alla semicirconferenza rispettivamente nei punti F e G e tale che la
proiezione di V sulla base AB coincida con O. Detto P un punto dell’arco FG e, rispettivamente, L e
M le intersezioni della tangente alla semicirconferenza in P con i lati AV e BV, si dimostri che i
triangoli AOL e BMO sono simili.
Indicato con x uno degli angoli alla base del triangolo ABV, si esprima in funzione di esso la
somma s tra il lato del quadrato equivalente al rettangolo di lati AL e BM e l’altezza VO del
triangolo ABV, spiegando perché s non dipende dalla posizione del punto P.
Si dimostri che s è minima per x = .
4
Indicazioni per la valutazione:
Passo risolutivo del problema
1 Figura corretta e utile alla risoluzione del problema
2 Dimostrazione che i triangoli AOL e BMO sono simili
3 Calcolo di OB, AO e VO
4 Campo di variazione di x, espressione di s in funzione
di x, spiegazione del fatto che s è indipendente da P
5
Dimostrazione che s è minima per x =
4
Competenze interessate
Comprendere un testo
Dimostrare
Misurare e calcolare
Modellizzare
Valutazione
Dimostrare,
modellizzare, misurare e
calcolare
Suggerimento per la risoluzione: si noti che non è necessario svolgere il punto 2 per proseguire: è
possibile assumere che AOL e BMO sono simili e proseguire nel compito (lasciando eventualmente
le dimostrazioni alla fine)
Compito 11.
Risolvere le seguenti disequazioni negli intervalli a fianco indicati
) + cos ( x - ) > 1
4
4
2
2. sen (2x) – cos x + cos(2x) > 0
3. sen2 (x/2) + cos x < 1
4. sen(x - /3) > cos (x + /4)
1. sen (x -
[- , ]
[- /2 , /2]
[0 , 2 ]
[0, 2 ]
per la sufficienza è necessario svolgere almeno due esercizi completamente e senza errori
Competenze interessate:
a) comprendere un testo b) calcolare
Compito 12.
In una semicirconferenza di centro O e raggio e diametro AB = 2r, si inscriva il triangolo ABD,
retto in D. Tracciare la bisettrice dell’angolo DAB; tale bisettrice intersechi il segmento BD in E.
Indicando con x l’angolo BAE, determinare la radice quadrata del rapporto tra la lunghezza del
BE
segmento BE e la lunghezza del segmento BD. Sia y =
.
BD
Si dimostri che ogni angolo alla circonferenza che insiste sulla corda AD misura 2 x .
2
Disegnare il grafico della funzione y = f(x) nell’intervallo ] 0 ,
[.
4
Indicazioni per la valutazione:
Passo risolutivo del problema
1 Figura corretta e utile alla risoluzione del problema
2 Dimostrazione
3 Espressione di BE in funzione di x
4 Espressione di y in funzione di x
5 Disegno del grafico
Competenze interessate Valutazione
Comprendere un testo
Dimostrare
Modellizzare e calcolare
Calcolare
Porsi
e
risolvere
problemi
Compito 13.
1. Risolvere graficamente, se possibile, le seguenti equazioni trigonometriche nell’intervallo [ ; ]
sin x = 1/3
cos x = 3/5
sin x = 3
2. Risolvere le seguenti equazioni trigonometriche determinando, se possibile, le soluzioni
esatte nell’intervallo [0; 2]
2
1
cos x = 2 sin x =
cos x =
2
2
3. Risolvere con la calcolatrice le seguenti equazioni trigonometriche determinando, se
possibile, le soluzioni nell’intervallo [- ; ] con quattro cifre decimali
sin x = 0,8
cos x = - 1,2
cos x = -0,75
4. Determinare graficamente l’angolo ottuso per cui sin x = 1/3. Quanto vale il coseno di tale
angolo?
5. Risolvi nell’intervallo [0; 2] l’equazione cos2 x – sin x = - 1
6. Che cosa si può dire delle relazioni che legano sin (x - ) e cos ( - x) a sin x e a cos x?
2
2
Giustificare la risposta.
7. Utilizza la calcolatrice per determinare sin x per x che si avvicina sempre di più a 0. Parti,
per esempio, da x = 1 e riduci ogni volta x della metà. Che cosa succede dopo cinque o sei
passi? Prova a dare una giustificazione di tale fatto.