Geometria piana: applicazione del primo criterio di congruenza
Sul triangolo Isoscele
Problema
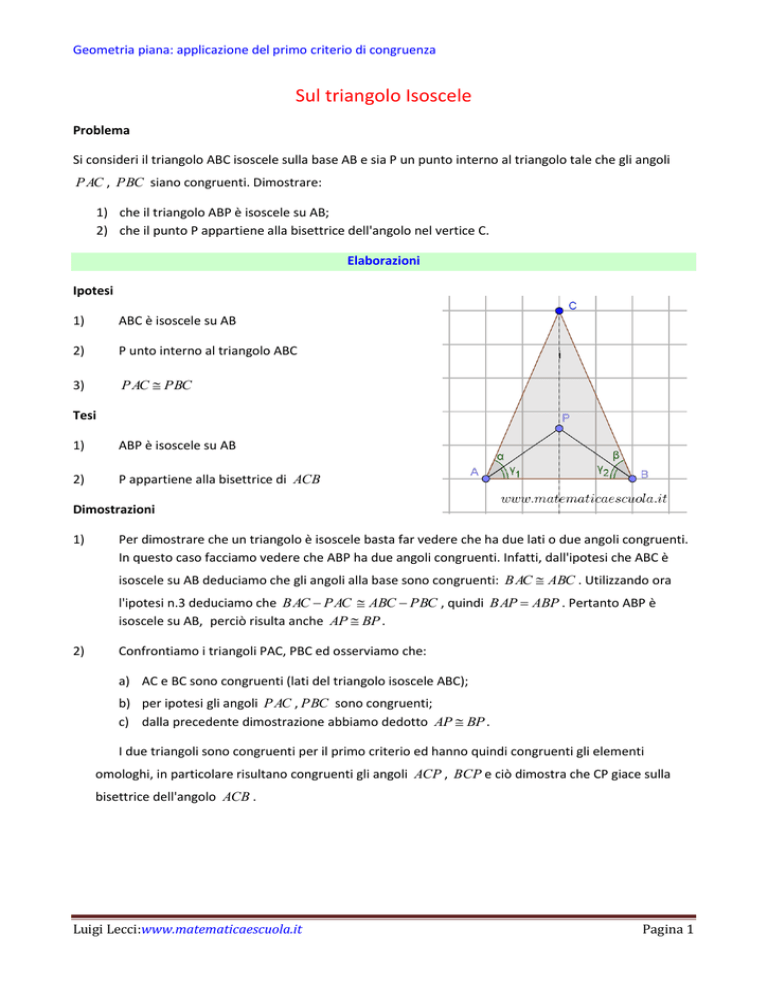
Si consideri il triangolo ABC isoscele sulla base AB e sia P un punto interno al triangolo tale che gli angoli
P AC , PBC siano congruenti. Dimostrare:
1) che il triangolo ABP è isoscele su AB;
2) che il punto P appartiene alla bisettrice dell'angolo nel vertice C.
Elaborazioni
Ipotesi
1)
ABC è isoscele su AB
2)
P unto interno al triangolo ABC
3)
PAC PBC
Tesi
1)
ABP è isoscele su AB
2)
P appartiene alla bisettrice di ACB
Dimostrazioni
1)
Per dimostrare che un triangolo è isoscele basta far vedere che ha due lati o due angoli congruenti.
In questo caso facciamo vedere che ABP ha due angoli congruenti. Infatti, dall'ipotesi che ABC è
isoscele su AB deduciamo che gli angoli alla base sono congruenti: BAC ABC . Utilizzando ora
l'ipotesi n.3 deduciamo che BAC PAC ABC PBC , quindi BAP ABP . Pertanto ABP è
isoscele su AB, perciò risulta anche AP BP .
2)
Confrontiamo i triangoli PAC, PBC ed osserviamo che:
a) AC e BC sono congruenti (lati del triangolo isoscele ABC);
b) per ipotesi gli angoli P AC , PBC sono congruenti;
c) dalla precedente dimostrazione abbiamo dedotto AP BP .
I due triangoli sono congruenti per il primo criterio ed hanno quindi congruenti gli elementi
omologhi, in particolare risultano congruenti gli angoli ACP , BCP e ciò dimostra che CP giace sulla
bisettrice dell'angolo ACB .
Luigi Lecci:www.matematicaescuola.it
Pagina 1












