Marco Mantovani
PROBLEMA: Costruzione con riga e compasso
Costruire il triangolo ABC dati i lati AB ed AC e la bisettrice dell'angolo interno BAC.
E
A
B
C
D
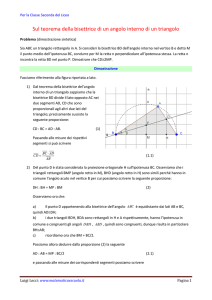
Sia dato il triangolo ABC in figura, dove AD è la bisettrice dell’angolo BAC. Sono dati
AB=a, AD=b ed AC=c.
Dal punto C, si traccia la retta parallela alla bisettrice AD e si individua il punto E,
intersezione di tale retta con il prolungamento del segmento AB. Considerate le due
rette parallele AD e CE, intersecate dalla trasversale BE, gli angoli BAD e BEC sono
congruenti perché corrispondenti. Inoltre, considerate le due rette parallele AD e CE,
intersecate dalla trasversale AC, gli angoli DAC e ACE sono congruenti perché alterni
interni. Perciò, essendo l’angolo BAD congruente all’angolo DAC (per ipotesi, dal
momento che AD è bisettrice dell’angolo BAC), il triangolo ACE è isoscele perché ha gli
angoli alla base CE congruenti. Ne segue che i lati AC e AE sono congruenti (ed è
AC=AE=c). Dalla similitudine dei triangoli BAD e BEC, si ottiene:
AB : AD = BE : CE
a : b = (a+c) : CE
Perciò si può costruire CE come quarto proporzionale tra a, b e (a+c), come illustrato in
figura.
a
c
a+c
CE
A questo punto, si può effettivamente pervenire alla costruzione del triangolo. Infatti, si
fissa il segmento CE a partire dal punto C. Poi si costruisce il triangolo isoscele di lati
uguali AC e AE (AC=AE=c), identificando il punto A. Poi si prolunga AE dalla parte di A
di un segmento pari a AB=a, identificando il punto B. I vertici A, B e C del triangolo
desiderato risultano così individuati.
FINE