PROBLEMI DI SCELTA IN CONDIZIONI DI INCERTEZZA,
CON EFFETTI IMMEDIATI
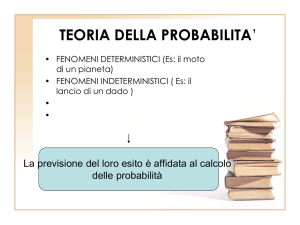
In problemi di questo tipo si opera una scelta tra più alternative , 1 ≤ ℎ ≤ , ma
il risultato non dipende dalla volontà di chi
effettua la scelta, in quanto ogni
alternativa è una variabile casuale1 che può assumere valori diversi in funzione del
verificarsi di uno tra gli eventi ad essa collegati. Gli eventi sono tra loro
incompatibili (il verificarsi di uno di essi esclude il verificarsi di tutti gli altri) e
complementari (la somma delle loro probabilità deve essere uguale a 1, e ciò
significa che uno di essi si verifica certamente).
Un problema di scelta in condizioni di incertezza con effetti immediati si rappresenta
mediante la seguente tabella, detta “ matrice o tabella dei risultati ” dove sono
le alternative ed sono gli eventi :
…...
……
……
……
………..
…….
……
……
……
……
……
Dall’esame della tabella si può vedere se vi è un’alternativa i cui valori sono migliori
dei corrispondenti di tutte le altre, per ogni evento, allora essa è senz’altro quella da
preferire (cioè se i suoi valori sono maggiori o uguali dei corrispondenti in caso
di massimo o guadagno, minori o uguali in caso di minimo o costo).
Analogamente un’alternativa è da scartare se i suoi valori sono peggiori dei
corrispondenti di tutte le altre (cioè maggiori o uguali in caso di minimo e minori o
uguali in caso di massimo).
Una grandezza si dice variabile casuale o aleatoria se assume determinati valori , , ⋯ , in funzione del
verificarsi di altrettanti eventi , , ⋯ , tra loro incompatibili e complementari dei quali sono note le
probabilità , , ⋯ , . Ovviamente deve essere: ∑
# = 1.
1
Un problema di scelta, in condizioni di incertezza e con effetti immediati, si può
risolvere con il “Criterio del valore medio” o della “Speranza matematica”, se agli
eventi è associata, o si può associare, una distribuzione di probabilità che verifica la
condizione:
& = 1
#
CRITERIO DEL VALORE MEDIO
Se agli eventi non è attribuita alcuna distribuzione di probabilità, si può effettuare una
valutazione soggettiva, cioè in base alle proprie convinzioni personali, tenuto conto
che l’individuo che ama il rischio sarà portato ad attribuire valori elevati alle
probabilità e quello prudente valori piuttosto bassi.
Il Criterio del valore medio consiste nel calcolare il valore medio ' di ogni
alternativa, per scegliere l’alternativa con valore medio maggiore in caso di massimo,
minore in caso di minimo.
' = & #
CRITERIO DEL PESSIMISTA
Si applica quando alla tabella dei risultati non è associata alcuna distribuzione di
probabilità e non la si vuole attribuire soggettivamente. Si parla, in tale caso, anche di
scelta in assenza di informazioni.
Il criterio del pessimista prende il nome di ” Criterio del maximin” in caso di
massimo o di utile (si prendono tutti i minimi e poi tra essi si sceglie il massimo).
Invece si parla di “Criterio del minimax” in caso di minimo (si prende il massimo di
ogni alternativa e tra essi si sceglie il minimo).
Esistono anche altri criteri come il maximax (massimo dei massimi in caso di utile)
ed il minimin (minimo dei minimi in caso di costo).
Applicazione.
Per la produzione di un bene un’impresa può utilizzare due macchine A e B.
− La macchina A richiede una spesa fissa mensile per la manutenzione e l’ammortamento di €1.400 e un costo di 2€ per ogni pezzo prodotto.
− La macchina B richiede una spesa fissa mensile per la manutenzione e l’ammortamento di 1.100 € e un costo di € 2,2 per ogni prezzo prodotto.
Il prezzo di vendita di ogni prezzo prodotto è di 5,6 €. In base ad esperienze
precedenti si valuta la seguente probabilità di vendita mensile relativamente al
numero dei pezzi.
N. pezzi
200
300
400
600
800
1000
1200
1400
1800
Probabilità
0,10
0,15
0,20
0,25
0,12
0,10
0,05
0,02
0,01
Determinare la soluzione più conveniente applicando il criterio del valore medio e, in
assenza di informazioni, il criterio del pessimista. Scriviamo le funzioni dell’utile:
(A): )*# 2x+1400
+* = 3,6x-1400
200
300
400
600
800
1000
1200
1400
1800
(B): ), = 2,2x+1100 +, = 3,4x- 1100
A
B
Pi
-680
40
760
1480
2200
2920
3640
4360
5080
-420
260
940
1620
2300
2980
3660
4340
5020
0,10
0,15
0,20
0,25
0,12
0,10
0,05
0,02
0,01
MA = - 680 ∙ 0,10 + 40 ∙ 0,15 + 760 ∙ 0,20 + 1480 ∙ 0,25 + 2200 ∙ 0,12 + 2920 ∙ 0,10 + 3640 ∙ 0,05
+ 4360 ∙ 0,02 + 5080 ∙ 0,01= - 68 + 6 + 152 + 370 + 264 + 292 + 182 + 87,2 + 50,8 = 1336
89 =420 · 0,10 + 260 · 0,15 + 940 · 0,20 + 1620 · 0,25 + 2300 · 0,12 + 2980 · 0,10 + 3660 · 0,05
+ 4340 · 0,02 + 5020 · 0,01 = - 42 + 39 + 188 + 405+ 276 + 198 + 183 + 86,8 + 50,2 = 1484
Conviene l’alternativa B.
Maximin
Alternativa (A): il minimo è – 680, Alternativa (B): il minimo è – 420, ⇒B