Monopolio naturale e struttura ottimale dei prezzi

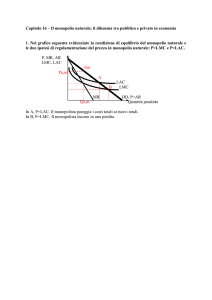
Monopolio naturale e struttura ottimale dei prezzi
Giuseppe De Feo e Alfredo Del Monte
Giugno 2012
Versione preliminare
non citare senza il permesso degli autori
Contents
1 Introduzione
2
2 Monopolio naturale
3
2.1
Un gioco di entrata in un monopolio naturale . . . . . . . . . . . . . . . . . . .
4
2.2
Subadditività . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.2.1
Un monopolista monoprodotto . . . . . . . . . . . . . . . . . . . . . . .
5
Il caso dell’impresa multiprodotto . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.3
3 Prezzi ottimali
8
3.1
Prezzo uguale al costo marginale . . . . . . . . . . . . . . . . . . . . . . . . . .
8
3.2
Regola di prezzo uguale a costo medio . . . . . . . . . . . . . . . . . . . . . . .
10
3.3
Prezzi à la Ramsey in un monopolio naturale multiprodotto. . . . . . . . . . .
11
3.3.1
Derivazione formale dei prezzi Ramsey . . . . . . . . . . . . . . . . . . .
14
3.4
Altri metodi di regolamentazione dei prezzi . . . . . . . . . . . . . . . . . . . .
16
3.5
Test sui sussidi incrociati . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
4 Prezzi non lineari
20
5 È sempre necessaria la regolamentazione del Monopolio naturale?
22
5.1
Il caso di un’impresa multiprodotto . . . . . . . . . . . . . . . . . . . . . . . . .
1
25
1
Introduzione
“[T]here is natural monopoly in a particular market if and only if a single firm can produce
the desired output at lower cost than any combination of two or more firms”. (Sharkey, 1982,
pag. 54)
Il concetto di monopolio naturale è il motivo principale utilizzato per giustificare l’intervento
pubblico diretto in industrie importanti come il settore energetico, le telecomunicazioni, i
trasporti e i servizi idrici. Quando un’industria è un monopolio naturale nasce una difficoltà
di conciliare l’efficienza allocativa e l’efficienza produttiva. Un’impresa monopolistica minimizza i costi di produzione ma, utilizzando il proprio potere di mercato può imporre un prezzo
superiore al costo marginale (inefficienza allocativa). Tuttavia se si introduce la concorrenza in
questo mercato l fine di raggiungere l’efficienza allocativa, il costo di produzione sarà inefficientemente più alto di quello ottenibile in regime di monopolio. In questo capitolo saranno definite
le condizioni necessarie per descrivere un’industria come un monopolio naturale. Discuteremo
sia il caso di un’impresa mono-prodotto che di un’impresa multi-prodotto. Il concetto centrale
utilizzato per caratterizzare l’industria come monopolio naturale è la subadditività della funzione di costo. Definiremo questo concetto paragonandolo ad altri concetti importanti come
le economie di scala e di scopo. L’approccio tradizionale della Teoria dell’Interesse Pubblico
era essenzialmente concentrato sull’identificazione delle strategie di prezzo ottimali che devono essere imposte al monopolista al fine di massimizzare il benessere sociale. Il problema
principale in questi mercati è che la regola del prezzo uguale al costo marginale, ottimale
in altri contesti, comporta perdite per l’impresa regolamentata. L’approccio del second best
(ottimo di secondo rango) ha l’obiettivo di identificare le strategie di prezzo che permettono
il raggiungimento di un’allocazione ottimale vincolata dove il vincolo viene dalla necessita di
portare i bilanci dell’impresa regolamentata in pareggio. In presenza di tale vincolo si genera solitamente una perdita netta di benessere sociale. Questo approccio ha un’applicazione
alquanto chiara nel caso di monopolista monoprodotto (prezzo uguale al costo medio), mentre
richiede approfondimenti analitici maggiori nel caso di impresa multiprodotto dove i prezzi
ottimi in presenza del vincolo di bilancio in pareggio sono detti prezzi à la Ramsey. Accanto
alla definizione di prezzi ottimi lineari, vi è la possibilità di considerare prezzi non lineari,
ovvero non proporzionali alla quantità acquistata. Analizzaremo il caso delle tariffe a due
parti (una fissa ed una proporzionale) e vedremo come questo tipo di tariffe ha la possibilità
2
di ripristinare l’efficienza allocativa anche in presenza di vincoli di bilancio. Tuttavia questo
è possibile solo se nessun consumatore viene escluso dall’acquisto del bene.
2
Monopolio naturale
Si dice che un’industria è caratterizzata da monopolio naturale quando una sola impresa
riesce a produrre il quantitativo di prodotto richiesto dal mercato a un costo inferiore a quello
ottenibile qualora esso fosse realizzato da due o più imprese. Il monopolio naturale caratterizza
numerosi settori produttori di pubblici servizi (telecomunicazioni, trasporti ferroviari, energia
elettrica ecc.)
La definizione di monopolio naturale deve essere approfondita. Una prima importante
dimensione da chiarire è relativa alla quantità richiesta dai consumatori. Ovviamente, questa
dipende dal prezzo di mercato che è influenzato dalla struttura del mercato e dal grado di
concorrenza che è a sua volta determinato dal numero di imprese sul mercato. Quindi non cè
nessun problema per definire un’industria monopolio naturale se il costo di produrre qualsiasi
quantità è minimizzato quando questa è prodotta da una sola impresa. Ma se l’industria è
un monopolio naturale solo per certi livelli di produzione, allora l’affermazione che si tratti
di un monopolio naturale deve essere qualificata e la sussistenza stessa di queste condizione è
soggetta ai cambiamenti delle condizioni di mercato sia sul lato della domanda che dell’offerta.
Il monopolio naturale è una delle cause di fallimento di mercato, ovvero una delle violazioni
delle assunzioni dei Teoremi Fondamentali dell’Economia del Benessere. Questa genera una
tensione tra efficienza allocativa ed efficienza produttiva. Infatti, se l’efficienza produttiva
è raggiunta quando una sola impresa soddisfa l’intera domanda di mercato, quest’impresa
monopolistica potra comunque utilizzare il proprio potere di mercato per fissare un prezzo superiore al costo merginale; questo genera una perdita di efficienza allocativa dovuta alla perdita
secca di benessere sociale che si genera in questo caso. Dall’altro lato, se più imprese competono sul mercato caratterizzato come monopolio naturale, il prezzo diventa maggiormente
allineato con il costo marginale di produzione, ma la produzione viene ad essere effettuata ad
un costo maggiore di quello di un monopolista, perdendo quindi efficienza produttiva. Come
evidenziato dal seguente esempio, le forze di mercato da sole non sono in grado di risolvere
questa tensione. Normalmente la risposta dei governi a tale situazione è sta quella di utilizzare
l’intervento pubblico, attraverso la produzione diretta o la regolamentazione, per cercare di
3
Impresa 1
Entrare
Restare fuori
Impresa 2
Entrare
−k, −k
Restare fuori
Entrare
Πm , 0
0, Πm
Restare fuori
0, 0
Figure 1: Il gioco di entrata in un monopolio naturale con due imprese
bilanciare in maniera ottimale l’efficienza allocativa e quella produttiva.
2.1
Un gioco di entrata in un monopolio naturale
Si consideri il caso in cui n imprese siano disposte ad entrare sul mercato e a produrre un
bene omogeneo la cui tecnologia produttiva è definita dalla seguente funzione di costo Ci (qi ) =
k + cqi . Questa industria è un monopolio naturale in quanto per ogni q il costo di produzione
è minimizzato quando è un’unica impresa a produrre l’intera quantità. Sia p (Q) la funzione
P
di domanda inversa con p′ (Q) < 0 e sia Q = ni=1 qi la quantità totale prodotta da tutte le
imprese che entrano sul mercato.
Si consideri il seguente gioco a due stadi in cui:
1o stadio Possibili entranti decidono indipendentemente e simultaneamente se entrare o meno
nel mercato; se decidono di entrare devono sostenere un costo fisso di entrata k che non
è recuperabile in caso di uscita.
2o stadio m le imprese che entrano sul mercato competono scegliendo simultaneamente ed
indipendentemente il prezzo per un bene omogeneo.
(concorrenza à la Bertrand)
Il gioco è descritto (in forma ridotta) nella Figura 2.1 per il caso in cui ci sono solo due
imprese che vogliono entrare sul mercato. L’equilibrio perfetto nei sottogiochi (EPS) di questo
gioco dinamico a due stadi si trova applicando l’induzione a ritroso.
4
Nel secondo stadio il payoff di ciascuna impresa dipende dal numero delle imprese che
entrano nel mercato. Se due o più imprese entrano, la competizione à la Bertrand porta a
p = c e Πi = −k per tutte le imprese che decidono di entrare, mentre quelle che decidono
di non entrare ottengono profitti nulli. Al contrario, se una sola impresa entra sul mercato
potrà chiedere un prezzo di monopolio e guadagnare i profitti di monopolio, mentre le altre
che decidono di restar fuori dal mercato ottengono profitti nulli.
Nel primo stadio del gioco, se due o più imprese entrano sul mercato, ciascuna di esse
ottiene profitti negativi dato l’equilibrio nello stadio 2. Tale combinazione di strategie delle
imprese non può essere un equilibrio in quanto ciascuna impresa preferirebbe restare fuori
dal mercato piuttosto che fare perdite entrando. Solo l’allocazione in cui una delle imprese
entra sul mercato e le altre stanno fuori può essere un equilibrio (in strategie pure). Infatti
per l’impresa che entra i profitti non possono essere maggiori di quelli ottenuti in monopolio,
mentre le altre che restano fuori non possono far meglio cambiando strategia. Di conseguenza
l’equilibrio perfetto nei sottogiochi è quello in cui una sola impresa entra sul mercato e sceglie
prezzi di monopolio. Tuttavia, questo equilibrio genera un’allocazione delle risorse che è
inefficiente dal punto di vista allocativo, visto che il prezzo sarà quello di monopolio.
2.2
Subadditività
La condizione più generale per definire un monopolio naturale è definita in temini di costi
dell’impresa.
Definizione 1 (Subadditività) Un’industria è definita monopolio naturale se la funzione
di costo dell’impresa è subadditiva per la quantità domandata dal mercato. In tal caso si ha
efficienza produttiva solo quando un’unica impresa, un monopolio, produce l’intera quantità.
Al fine di applicare il concetto di subadditività dobbiamo distinguere il caso di un’impresa che
produce un singolo prodotto, da quello in cui il monopolista è multiprodotto.
2.2.1
Un monopolista monoprodotto
Nel caso in cui l’impresa roduce un solo prodotto, la sua funzione di costo è subadditiva se
per la quantità Q se
C(Q) ≤ C(q1 ) + C(q2 )
5
∀q1 , q2 : q1 + q2 = Q
(1)
In altre parole, una funzione di costo è subadditiva al livello di produzione Q se il costo di
produrre Q in una sola impresa è inferiore a quello di suddividere la produzione tra due (o
più) imprese, indipendentemente dal modo in cui Q è diviso tra le imprese.
È interessante paragonare la subadditività della funzione di costo con la presenza di
economie di scala.
Una tecnologia produttiva esibisce economie di scala per le quantità q ∈ [0, Q] se la funzione
di costo è tale che
tC (Q) ≤ C (tQ) ∀t ∈ (0, 1]
(2)
È semplice verificare graficamente (Figura 2.2.1) che la presenza di economie di scala
implica la subadditività della funzione di costo, mentre il contrario non è necessariamente
vero. Si assuma, come in Figura 2.2.1 che la curva di costo medio AC1 è a forma di U, con un
costo medio minimo raggiunto alla quantità Q′ . Con due imprese attive sul mercato possiamo
raffigurare la curva di costo medio AC2 quando la quantità Q è ripartita equamente tra le due
imprese (ciascuna, cioè produce Q/2). In tal caso il costo medio minimo si ottiene quando la
produzione è pari a 2Q′ . È importante notare come la curva AC2 si trovi al di sopra della
curva AC1 per i livelli di produzione Q ∈ [0, Q⋆ ] con Q⋆ > Q′ . Queso significa che è meno
costoso produrre con una impresa che con due o più imprese qualsiasi quantità compresa tra
0 and Q⋆ .1
Utilizzando la definizione data sopra, possiamo dire che la funzione di costo C (.) è caratterizzata da economie di scal nell’intervallo [0, Q′ ], mentre è subadditiva nell’intervallo [0, Q⋆ ]
with Q⋆ > Q′ . Quindi, per ogni quantità Q ∈ [Q′ , Q⋆ ] la funzione di costo è subadditiva anche
se la produzione è caratterizzata da diseconomie di scala.
2.3
Il caso dell’impresa multiprodotto
In mercati caratterizzati da monopolio naturale, le imprese di solito producono più di un unico
prodotto. Se per esempio l’impresa produce i prodotti A e B, la funzione di costo è subadditiva
in QA , QB se
1
C QA , QB ≤ C q1A , q1B + C q2A , q2B
∀q1i , q2i : q1i + q2i = Qi con i = A, B.
(3)
È intuitivo che se la quantità è divisa tra tre o più imprese la curva di costo medio si troverà al di sopra
della curva di costo AC1 per una quantità ancora più ampia.
6
Figure 2: Economie di scala e subadditività della funzione di costo (Viscusi et al., 2004).
In altre parole, una funzione di costo è subadditiva per le quantità QA , QB se queste quantità
non possono essere prodotte ad un costo minore da due o più imprese, indipendentemente da
come il prodotto sia ripartito tra le imprese.
Nel caso di impresa multiprodotto, la tecnologia produttiva può essere caratterizzata non
solo da economie di scala, ma anche da quelle di scopo.
Una tecnologia produttiva è caratterizzata da economie di scopo se è meno costoso produrre
i due beni insieme nella stessa impresa, piuttosto che separatamente in due o più imprese.
Inoltre una funzione di costo è caratterizzata da economie di scala per le quantità QA , QB
se è meno costoso produrre le quantità dei due beni insieme piuttosto che in due o più imprese
diverse.
In termini analitici ci sono economie di scopo se:
C QA , QB ≤ C QA , 0 + C 0, QB
(4)
Con un’impresa multiprodotto ci sono delle economie di scala per le quantità Q ∈ 0, QA ×
0, QB se
tC QA , QB ≤ C tQA , tQB
∀t ∈ (0, 1]
(5)
7
3
Prezzi ottimali
Il monopolio naturale rappresenta un caso di fallimento del mercato perché il libero agire
del mercato non riesce a raggiungere un’efficiente allocazione delle risorse. Da un lato, se
l’equilibrio di mercato comporta che più di un’impresa sia attiva sul mercato, ciascuna di
essa produrrebbe a costi superiori a quelli di un monopolista. Dall’altro, se la produzione è
tutta realizzata da una sola impresa, la massimizzazione dei profitti porterà questa impresa
a imporre un prezzo di monopolio che genera extraprofitti per le imprese, ma sopratutto una
produzione subottimale con perdita di benessere sociale. Quindi il monopolio naturale genera
una tensione tra efficienza allocativa ed efficienza produttiva che l’intervento regolatore dei
poteri può potenzialmente alleviare.
La soluzione proposta dalla teoria dell’interesse pubblico identificavo come strumento di regolamentazione l’imposizione di prezzi da parte di un’autorità di regolamentazione all’impresa
monopolista. Quindi l’obiettivo della teoria economica è quello di identificare i prezzi ideali
che massimizzano il benessere sociale.
3.1
Prezzo uguale al costo marginale
La soluzione ottimale di primo rango (first best) che massimizza il surplus generato sul mercato
impone un prezzo uguale al costo marginale. Se solo un’impresa è attiva sul mercato, al fine
di evitare le inefficienze allocative create da politiche di prezzo monopolistiche, le autorità di
regolamentazione dovrebbero imporre un prezzo uguale al costo marginale. Questa soluzione,
supportata da tra gli altri da Hotelling (1938) e Vickrey (1948) ha tuttavia i suoi risvolti
negativi quando la produzione avviene in presenza di subadditività della funzione di costo: i
ricavi non coprono i costi di produzione e il deficit deve essere finanziato con mezzi alternativi,
come ad esempio sussidi governativi. Come risulta evidente dalla figura ??. in presenza di
condizioni di monopolio naturale la curva di costo marginale (MC) è sempre sottoposta alla
curva di costo medio (AC) e quindi quando P = M C si genera una perdita per l’impresa pari
all’area P0 ST R.
Quindi se si impone tare regola di prezzo, il monopolista deve essere sussidiato dal governo.
Ma il fatto che tale regola di prezzo richiede dei sussidi pubblici per essere sostenuta, è un
aspetto negativo da considerare, in quanto questi sussidi devono essere finanziati attraverso
tasse dirette o indirette che a loro volta generano distorsioni e inefficienze in altri mercati. Se
8
Figure 3: Una politica di prezzo uguale costo marginale comporta perdite per l’impresa in
monopolio naturale (Viscusi et al., 2004).
non sono disponibili tasse non distorsive (in somma fissa), infatti, le tasse indirette introducono
una differenza tra costo e prezzo in altri mercati, e quindi una inefficienza dello stesso tipo
di quella che si vuole evitare sul mercato caratterizzato da monopolio naturale. Un discorso
analogo può farsi per le tasse dirette sul reddito che possono generare distorsioni nelle scelta
tra consumo e risparmio e nella scelta del paniere di beni da acquistare.
Altre obiezioni sono state fatte alla regola del prezzo uguale al costo marginale. Ad esempio, da un punto di vista redistributivo non sembra esserci un motivo chiaro che giustifichi il
fatto che contribuenti che non acquistano il servizio fornito in condizioni di monopolio naturale debbano sussidiare gli acquirenti di tale servizio. Inoltre può essere politicamente difficile
sostenere che i contribuenti debbano finanziare un’impresa privata. Infine in presenza di informazione imperfetta sui costi di produzione, tale regola può rappresentare un disincentivo per
il management alla riduzione dei costi e all’efficienza produttiva visto che le perdite vengono
comunque ripianate dal governo che ha difficoltà a distinguere le perdite derivanti dalla regola
del prezzo pari al costo marginale da quelle derivanti da inefficienza produttiva.
9
3.2
Regola di prezzo uguale a costo medio
Dati i problemi sollevati dalla necessità di sussidiare un’impresa in monopolio naturale quando
si applica la regola di prezzo uguale costo marginale, diventa necessario identificare una
soluzione alternative che può essere effettivamente molto intuitiva: scegliere una regola di
prezzo che massimizza il benessere sociale sotto il vincolo che non vi siano perdite per il
monopolista. Questa regola tuttavia si discosta dalla soluzione di ottimo di primo rango in
quanto il vincolo di bilancio impedisce di scegliere un’allocazione ottimale delle risorse e viene
definita come regola ottimale di secondo rango (second best).
A
B
C
Figure 4: Una politica di prezzo uguale costo medio comporta comunque una perdita netta di
surplus (Viscusi et al., 2004).
Nel caso in cui il monopolista sia monoprodotto questa coincide con la regola di prezzo
uguale costo medio, la quale assicura che il monopolista possa produrre la quantità richiesta
dal mercato ad un prezzo che non necessita alcun sussidio. Tuttavia, come mostrato nella
Figura 3.2, la regola di prezzo uguale costo medio crea una perdita di benessere sociale pari
all’area ABC. Infatti, la quantità [Q0 , Q⋆ ] potrebbe essere prodotta ad un costo inferiore
alla disponibilità a pagare dei consumatori. Tuttavia, a causa della presenza di rendimenti
crescenti i ricavi totali sarebbero inferiori ai costi in quanto il prezzo diventerebbe inferiore al
costo medio.
10
3.3
Prezzi à la Ramsey in un monopolio naturale multiprodotto.
L’applicazione della regola uguale costo medio ha tuttavia difficoltà di applicazione al contesto
di un monopolista multiprodotto. Da un lato tale regola non dà alcuna indicazione circa il
modo di allocare i costi comuni tra i prezzi dei diversi beni prodotti. Dall’altro lato, uguagliare
il prezzo al costo medio del rispettivo prodotto può non essere ottimale. Anzi è generalmente
non ottimale in quanto non tiene conto della domanda. La soluzione ottimale di secondo rango
è stata individuata da Ramsey (1927) e Boiteux (1956). I prezzi à la Ramsey costituiscono la
soluzione ottimale di secondo rango in quanto minimizzano la perdita di benessere dovuta al
fatto che comunque i prezzi devono essere superiori al costo marginale quando cè da soddisfare
il vincolo del pareggio di bilancio in un monopolio naturale.
La soluzione può essere compresa meglio se iniziamo dal modo in cui il monopolista non
regolamentato definisce i prezzi che massimizzano i propri profitti.
Si consideri un monopolista che produce n beni o servizi in mercati caratterizzati da
domanda decrescente nei prezzi di ciascun prodotto. Si supponga inoltre che la domanda di
ciascun bene sia indipendente da utte le altre e che quindi le elasticità incrociate dei prezzi
siano nulle. Il problema del monopolista è quindi:
max
{pi }i=1,...,n
n
X
pi qi (pi ) − c (q1 , ..., qn )
i=1
Le condizioni del primo ordine (first order condition, FOC) per ciascun bene sono date da:
qi (p⋆i ) + p⋆i qi′ (p⋆i ) −
Sia c′i (.) =
∂c(q1 ,...,qn)
∂qi
∂c (q1 , ..., qn ) ′ ⋆
qi (pi ) = 0
∂qi
(6)
per rendere più agevole la scrittura, cosicché la FOC (6) può essere
riscritta cosı̀:
qi (p⋆i ) = − p⋆i − c′i (.) qi′ (p⋆i )
Moltiplicando entrambi i lati dell’equazione (7) per
p⋆i
qi (p⋆i )
p⋆i = p⋆i − c′i (.) ηi
(7)
otteniamo
(8)
pi
i (pi )
dove ηi = − ∂q∂p
qi (pi ) è l’elasticità della domanda per il prodotto i in valore assoluto. Quindi,
i
il monopolista multiprodotto massimizza i suoi profitti definendo un prezzo tale per cui l’indice
11
di Lerner è pari all’inverso dell’elasticità della domanda per ciascun prodotto i; cioè,
L⋆i =
1
p⋆i − c′i (.)
=
⋆
pi
ηi
(9)
La regola di Ramsey è la soluzione al seguente problema di massimizzazione del benessere
sociale sotto il vincolo di bilancio in pareggio, ovvero:
max W (p1 , ..., pn ) tale che
pi
n
X
pi qi − c (q1 , ..., qn ) ≥ 0
(10)
i=1
La soluzione di questo problema è tale per cui il surplus totale raggiunge il suo livello
SB . Quindi il problema (10) è
di ottimo di secondo rango, ovvero: W SB = W pSB
1 , ..., pn
equivalente al seguente problema che consiste nel massimizzare il profitto dellimpresa sotto il
vincolo che il benessere sociale non sia minore del livello ottimo di secondo rango.
max
pi
n
X
pi qi − c (q1 , ..., qn ) tale che W (p1 , ..., pi , ..., pn ) ≥ W RB
(11)
i=1
È possibile mostrare che la soluzione è simile a quella ottenuta nel caso di massimizzazione
libera dei profitti; essa infatti è:
LSB
=
i
pSB
− c′i
k
i
∀i dove k < 1 è una costante.
=
SB
ηi
pi
(12)
Questo significa che la struttura dei prezzi è la stessa sia nel monopolio regolamentato che in
quello non regolamentato. Infatti il rapporto tra gli indici di Lerner relativi a due beni è, sia
nel caso di monopolio regolamentato che non regolamentato, pari al rapporto inverso tra le
elasticità della domanda. Con qualche approssimazione, possiamo dire che i prezzi di Ramsey
sono gli stessi di quelli di un monopolista non regolamentato, solo più bassi.
Una caratteristica importante dei prezzi à la Ramsey è che il markup è maggiore per
domande più rigide e minore per domande più elastiche. La logica è chiara: si supponga
che dei costi fissi devono essere recuperati definendo dei prezzi maggiori dei costi marginali
per i beni prodotti da un monopolista naturale. In tal caso è meglio aumentare di più i
prezzi dei beni che hanno una domanda meno elastica in quanto la quantità acquistata si
riduce meno rispetto agli altri beni e di conseguenza si genera una perdita di benessere sociale
inferiore. Questo significa inoltre che più necessario è l’acquisto di quel bene e più alto sarà
il markup. Di conseguenza la regola di Ramsey genera qualche preoccupazione dal punto di
vista redistributivo. Tuttavia è utile qui ricordare che la teoria dell’interesse pubblico era solo
12
interessata a questioni di efficienza, lasciando alla politica il compito di risolvere i problemi
redistributivi.
Un’altra importante caratteristica dei prezzi Ramsey è il fatto che i costi sono essenzialmente messi tutti insieme e recuperati in modo da considerare solo le elasticità della domanda
dei diversi prodotti. Quindi un certo livello di sussidi incrociati comunque si determina in
quanto la corrispondenza tra prezzi e costi di produzione è mitigata.
Infine è bene enfatizzare che la soluzione presentata riguarda il caso di beni con domanda
indipendente; se le elasticità incrociate non sono nulle allora questa interdipendenza deve
essere tenuta in considerazione. Una descrizione intuitiva della direzione dei cambiamenti indotti dall’introduzione delle elasticità incrociate è la seguente. Se il prodotto i è sostituto del
prodotto j, un aumento in pj ha un effetto positivo sulla domanda di i, attenuando quindi
l’effetto negativo sul surplus sociale. Di conseguenza i prezzi per i beni sostituti dovrebbero
essere più alti rispetto a quelli per beni indipendenti. Il ragionamento simmetricamente opposto porta alla conclusione che il prezzo per beni complementari deve essere più basso di
quello definito nell’equazione(12).2
Con costi marginali costanti e funzioni di domanda lineare i prezzi Ramsey possono essere
ottenuti utilizzando la semplice formula:
qi pSB
q (c′ )
i
= i i .
qj pSB
qj c′j
j
(13)
Infatti è sufficiente calcolare la domanda quando il prezzo è uguale al costo marginale per i due
beni e quindi aumentare i prezzi fino al livello in cui il bilancio del monopolista è in pareggio
avendo cura di mantenere la proporzione tra le quantità vendute dei due beni. Si consideri
l’esempio seguente dove i costi e la domanda dei due beni sono rispettivamente:
c (q1 , q2 ) = 1050 + 20q1 + 20q2
2
(14)
q1 = 100 − p1
(15)
q2 = 120 − 2p2
(16)
Se tutti i beni prodotti dal monopolista sono sostituti, allora i prezzi dei beni con i sostituti più vicini
dovrebbero essere più elevati, mentre quelli dei beni con sostituti pi‘u lontani dovrebbero essere più bassi di
quelli definiti nell’equazione (12). Se tutti i beni sono complementi si applica il ragionamento diammetralmente
opposto.
13
Per calcolare i prezzi Ramsey possiamo utilizzare la semplice regola definita dall’equazione
(13) insieme al vincolo di bilancio in pareggio.
q1 pSB
80
q (20)
1
= 1
= q SB
= q2 pSB
=
= 1 =⇒ q1 pSB
2
1
SB
q2 (20)
80
q 2 p2
SB
SB
pSB
+ pSB
= 1050 + 20q1 pSB
+ 20q2 pSB
1
2
1 q 1 p1
2 q 2 p2
(17)
(18)
Dall’equazione (17) otteniamo che q1 = q2 nell’allocazione ottimale di secondo rango (second
best o SB). Sostituendo questa uguaglianza nel vincolo di bilancio (18):
SB
SB
pSB
+ pSB
= 1050 + 20q SB + 20q SB .
1 q
2 q
Sostituendo le funzioni di domanda inversa derivate
SB
1 SB SB
SB
100 − q
q
q + 60 − q
2
3 SB SB
160 − q
q
2
3 SB 2
q
− 1050
120q SB −
2
(19)
dall’equazione (15) e (16):
= 1050 + 20q SB + 20q SB
(20)
= 1050 + 40q SB
(21)
= 0.
(22)
Il polinomio ordinato di secondo grado ha due soluzioni:
SB
q− = 10; q+
= 70.
(23)
La seconda soluzione è quella che massimizza il benessere sociale sotto il vincolo del bilancio in pareggio ed è quindi corrisponde ai prezzi Ramsey per i due beni. I prezzi Ramsey
corrispondenti sono:
SB
pSB
1 = 30; p2 = 25.
3.3.1
(24)
Derivazione formale dei prezzi Ramsey
In ciò che segue i prezzi Ramsey sono derivati formalmente dal programma di massimizzazione
vincolata del benessere sociale. Ricordando che i prezzi Ramsey massimizzano il benessere
sotto il vincolo del bilancio in pareggio:
max W (p1 , ..., pn ) s.t. Π (p1 , ..., pn ) ≥ 0
pi
Il benessere totale può essere definito come la somma del surplus del consumatore e dei profitti
dell’impresa, quindi:
14
max CS (p1 , ..., pn ) + Π (p1 , ..., pn ) s.t. Π (p1 , ..., pn ) ≥ 0.
pi
Usando il metodo di Lagrange il problema precedente è equivalente alla massimizzazione della
seguente funzione Lagrangiana
L (p1 , ..., pn ) = CS (p1 , ..., pn ) + (1 + λ) Π (p1 , ..., pn )
Le condizioni del primo ordine sono:
∂L (.)
∂CS (p1 , ..., pn )
∂Π (p1 , ..., pn )
=
+ (1 + λ)
= 0 ∀i = 1, ...n.
∂pi
∂pi
∂pi
Ora, supponiamo che le domande dei beni prodotti dal monopolista sono indipendenti l’una
dall’altra. Possiamo allora facilmente calcolare le derivate parziali del surplus del consumatore
rispetto ai prezzi:
CS (p1 , ..., pn ) =
n
X
CSi (pi )
Z
qi (pi ) dp
i=1
p
CSi (pi ) =
∂CS (p1 , ..., pn )
∂pi
=
pi
∂CSi (pi )
= −qi (pi ) .
∂pi
L’intuizione per il risultato è la seguente: un incremento marginale del prezzo ha solo un effetto
del secondo ordine sulla quantità acquistata, ma un effetto del primo ordine sulla rendita che
passa dal consumatore all’impresa. Ha una magnitudine pari alla quantità acquistata, ma
ha segno opposto, in quanto un incremento del prezzo riduce il surplus del consumatore. Per
quanto riguarda i profitti dell’impresa, sotto le stesse assunzioni di indipendenza delle funzioni
di domanda:
Π (p1 , ..., pn ) =
n
X
pi qi (pi ) − c (q1 (p1 ) , ..., qn (pn ))
i=1
∂Π (p1 , ..., pn )
∂pi
∂c(.) ∂qi (pi )
= q i + pi −
.
∂qi
∂pi
Sostituendo le derivate parziali nelle condizioni del primo ordine della funzione Lagrangiana:
∂c(.) ∂qi (pi )
∂L (.)
= −qi (pi ) + (1 + λ) qi + pi −
= 0
∂pi
∂qi
∂pi
∂c(.) ∂qi (pi )
(1 + λ) qi + pi −
= qi (pi )
∂qi
∂pi
15
Moltiplicando il lato destro e quello sinistro per
pi
qi (pi )
pi
i (pi )
e poiché ηi = − ∂q∂p
qi (pi ) è l’elasticità
i
della domanda peril prodotto i in valore assoluto:
pi
∂c(.) ∂qi (pi )
(1 + λ) qi + pi −
∂qi
∂pi
qi (pi )
∂c(.)
(1 + λ) pi − (1 + λ) ηi pi −
∂qi
∂c(.)
− (1 + λ) ηi pi −
∂qi
pi − c′i (.)
pi
pi − c′i (.)
pi
= qi (pi )
pi
qi (pi )
= pi
= −λpi
=
=
λ 1
1 + λ ηi
k
λ
where k =
.
ηi
1+λ
Quando λ = 0 abbiamo che pi = c′i (.); ovvero, se il vincolo di bilancio non è stringente la
massimizzazione del surplus totale impone che il prezzo sia uguale al costo marginale, e si
raggiunge l’allocazione ottima di primo rango. Per comprendere ciò si consideri il caso di costi
marginali crescenti: i prezzi Ramsey corrispondono alla regola prezzo uguale costo marginale
poiché l’impresa ha profitti positivi nell’allocazione ottima di primo rango. Si deve notare che
in presenza di costi marginali crescenti non c’è problema di monopolio naturale.
3.4
Altri metodi di regolamentazione dei prezzi
Uno dei metodi utilizzati, allorché un’impresa regolamentata produce più di un prodotto
o vende a differenti classi di consumatori, è quello del prezzo basato sul costo permanente
distribuito (FDC). Esso permette di ripartire i costi comuni fra le varie classi o servizi.
Assumiamo che le funzioni di costo siano le seguenti:
• Produzione del bene 1
C(q1 ) = 700 + 20q1
• Produzione del bene 2
C(q2 ) = 600 + 20q2
• produzione congiunta dei beni 1 e 2
C(q1 ) = 1050 + 20q1 + 20q2
16
La funzione di costo dei due beni è subadditiva e 1050 è il costo da distribuire fra i
due beni in base al metodo FDC. In base a tale metodo i costi possono essere distribuiti
fra i due prodotti in base a qualche misura fisica di utilizzazione dell’impianto, ad esempio
tempo di utilizzo dei circuiti, o si può imputarli proporzionalmente ai costi che possono essere
direttamente assegnati ai vari servizi.
Questo metodo in realtà è arbitrario, cioè non ha una base teorica e l’allocazione del costo
comune fra i due prodotti non ha alcuna relazione con i costi marginali.
Assumiamo che, in base al tempo di utilizzo, si sia deciso che il 75% dei costi comuni deve
essere attribuito al prodotto 1 ed il 25% al prodotto 2. Quindi il costo medio dei due beni
sarà dato da:
787, 5
+ 20
q1
262, 5
+ 20
AC2 =
q2
AC1 =
Il costo medio di q1 sarà pari al 75% del costo comune diviso le unità vendute, più il costo
variabile per unità di prodotto che è pari a 20. Ragionamento analogo vale per il bene 2.
Consideriamo ora la curva di domanda dei due prodotti
P1 = 100 − q1 e P2 = 60 − 0, 5q2
I prezzi P1 e P2 si ottengono eguagliando il prezzo con il costo medio, in modo tale che
l’impresa regolamentata abbia il bilancio in pareggio. I valori ottenuti saranno
P1 = AC1 = 31, 5
e P2 = AC2 = 23, 6
Il rusultato è il seguente:
F DC
q1
= 68, 5
e
F DC
q2
= 72, 8
Abbiamo invece visto in precedenza nella Sezione 3.3 che i prezzi Ramsey relativi a tale
esempio sono P1 = 30 e P2 = 25. Da un punto di vista di efficienza il metodo corretto da
utilizzare per distribuire i costi fissi fra i prodotti è quello basato sui prezzi Ramsey. Il valore
dei prezzi utilizzando il metodo FDC porta invece a prezzi diversi dai prezzi Ramsey e quindi
tale metodo comporta una struttura dei prezzi non efficienti.
17
3.5
Test sui sussidi incrociati
Fino a tutti gli anni ‘70 la struttura dei prezzi dei servizi regolamentati era ben lungi dall’osservare
la regola dei prezzi Ramsey. Infatti, obiettivo del regolamentatore era che per motivi di equità, alcune fasce di consumatori dovessero godere di tariffe particolarmente favorevoli. Ciò
comporta che alcune fasce di consumatori, o di servizi, sussidino altre fasce di consumatori
o servizi. L’idea era che ogni cittadino aveva diritto a godere di tali beni indipendenti dalla
localizzazione e dal reddito per motivi sociali. Questo obiettivo, ad esempio, portava ad estendere la rete telefonica anche ad aree marginali senza che il costo di allacciamento richiesto al
consumatore permettesse di recuperare tutti i costi. Nonostante tale approccio da un punto di
vista economico fosse inefficiente, esso era giustificato in base a obiettivi distributivi. Fintanto
che l’impresa regolamentata era un’impresa pubblica la situazione era sostenibile in quanto la
raccolta delle tariffe era vista come una forma di tassazione. Introducendo la privatizzazione
e la concorrenza anche la struttura delle tariffe è destinata a cambiare. In questa fase è
importante poter individuare se una tariffa è sussidiata o meno.
Due sono i test usati dagli economisti per valutare se ci troviamo in presenza di prezzi
sussidiati. Il primo metodo è quello del costo da solo (CDS).
Questo test consiste nel confrontare il costo totale del servizio, nel caso fosse prodotto
per una sola fascia di consumatori, con il ricavo del servizio stesso ottenuto dalla vendita a
quella fascia di consumatori. Nel caso in cui per un servizio il ricavo è superiore al costo per
una fascia e inferiore per l’altra vi è un incentivo a produrre il bene solo nel primo caso e
non congiuntamente per le due fasce. Nel caso si produca per entrambe le fasce, la differenza
prezzo-costo serve a coprire le perdite che si hanno sulla tariffa praticata all’altra fascia di
consumatori.
Consideriamo il caso visto nella Sezione 3.4 dove prezzi e quantità sono stati definiti utilizzando il metodo del costo permanente distribuito (FDC). In tal caso le quantità prodotte
F DC
sono q1
F DC
= 68, 5 e q2
F DC
= 72, 8, mentre i prezzi sono P1
F DC
= 31, 5 e P2
= 23, 6.
Data la funzione di costo per la produzione isolata del bene 1
C(q1 ) = 700 + 20q1
F DC
avremo che per q1
F DC
= 68, 5 il costo totale sarà C(68, 5) = 2070, mentre i ricaviq1
18
F DC
×P1
=
2157 e la differenza ricavi costi
F DC
q1
F DC
× P1
F DC
− C(q1
) = 87
Data la funzione di costo per la produzione del bene2 da solo
C(q2 ) = 600 + 20q2
F DC
avremo che per q2
F DC
P2
F DC
= 72, 8 il costo totale sarà C(q2 ) = 2056, i ricavi saranno q2
×
= 1718 e la differenza ricavi costi
F DC
q2
F DC
× P2
F DC
− C(q2
) = −338.
In tal caso converrà produrre isolatamente il bene 1, e non produrre il bene 2. I prezzi
31,5 e 72,8 per X e Y comportano che il bene 2 sia sussidiato dal bene 1. Allorché l’impresa
produce a tali prezzi entrambi i beni, ottiene profitti nulli. Ripetendo lo stesso ragionamento
con i prezzi Ramsey in precedenza ottenuti, si ottiene un valore dei costi e dei ricavi per il
bene 1 eguale a 2160 e 2100. In modo analogo per il bene 2 si ottiene un costo totale di 2000
e ricavi totali pari a 1750.3 Quindi con i prezzi Ramsey non vi è alcun incentivo a produrre
uno dei due servizi isolatamente.
Un secondo test è quello del costo medio incrementale (AIC). In questo caso si calcola il
costo incrementale di produrre un dato bene. Nel caso in cui il prezzo di un bene è inferiore
all’AIC, significa che il bene è sussidiato. Calcoliamo l’AIC del bene 1, sottraendo il costo di
produzione del bene 2 (CDS) dal costo di produzione congiunto di 1 e 2.
AIC1 =
AIC2 =
(C12 −C2 )
q1
(C12 −C1 )
q2
F DC
Nel caso di prezzi FDC q1
=
=
1050+20q1 +20q2 −600−20q2
q!
1050+20q1 +20q2 −700−20q1
q2
F DC
= 68, 5 e P1
=
450
q!
+ 20
=
350
q2
+ 20
F DC
= 31, 5, e q2
F DC
= 72, 8 e P2
= 23, 6;
avremo che AIC1 = 26, 56 e AIC2 = 24, 8. Il prezzo di 2 è inferiore a AIC2 e quindi il bene 2
è sussidiato. Ci troviamo in un caso di sussidi incrociati.
In realtà una struttura che non è tipo prezzi Ramsey può non dar luogo a sussidi incrociati,
ma egualmente è inefficiente.
3
Giacché vi sono economie di scopo nella funzione dei costi, l’impresa realizzando congiuntamente i due beni
ha un risparmio di costi per cui l’impresa, come abbiamo visto, nel complesso non avrà perdite.
19
4
Prezzi non lineari
Prezzi non lineari permettono al monopolista di discriminare i consumatori in base alla quantità acquistata in quanto quantità diverse di un bene omogeneo vengono vendute a prezzi
unitari diversi. Una caratteristica di questa struttura dei prezzi è che essa può permette
di raggiungere una allocazione che, in presenza del medesimo vincolo di bilancio, genera un
surplus maggiore dei prezzi Ramsey.
Tuttavia, per applicare tariffe non lineari in modo da massimizzare il surplus sociale sono
necessarie più informazioni. La conoscenza dell’elasticità della domanda e della struttura dei
costi dell’industria può non essere abbastanza ed è in genere necessario avere informazioni
più precise sulle curve di domanda individuali. Questi requisiti aumentano le difficoltè per le
autorità di regolamentazione per l’implementazione di tariffe non lineari.
Si consideri il semplice caso di una tariffa non lineare che consiste in una somma fissa ed
un prezzo proporzionale alla quantità acquistata. La sua forma generale è:
T (q) = k + pq
(25)
Per illustrare la ragione per cui con tariffe non lineari è possibile approssimare la soluzione di
ottimo di primo rango, dimostreremo che è possibile avere un prezzo uguale al costo marginale
in un monopolio naturale ed avere il bilancio in pareggio allo stesso tempo.
Si consideri la tariffa a due parti T (q) definita nell’equazione (25) e considera l’esempio
illustrato in Figura 3.1. Quando il prezzo è uguale al costo marginale abbiamo visto che la
perdita per l’impresa è misurata dall’area P0 ST R. Definendo K la misura della perdita, se il
regolatore conosce il numero di consumatori, e questo è pari ad n, allora una tariffa a due parti
in cui la parte fissa k =
K
n
e la parte variabile p = M C annulla tutte le perdite di benessere
sociale e, allo stesso tempo, pareggia il bilancio dell’impresa. Questa tariffa ottimale si chiama
tariffa di Coase.
Il problema, in questa situazione, è che la parte fissa può escludere alcuni consumatori
dall’acquistare il servizio e può condurre ad inefficienze anche se ciascuna unità è venduta al
costo marginale.
Ad esempio assumiamo che le persone abbiano le stesse preferenze per il servizio e le
curve di domanda dei singoli consumatori siano abbastanza simili. In questo caso possiamo
ipotizzare che tutti i consumatori acquisteranno il servizio con una tariffa che richiede una
20
quota fissa pari a k =
K
n
ove n è il numero dei consumatori e p è il prezzo posto eguale al
costo marginale.
Nella Figura 3.1 osserviamo che se ogni consumatore paga k =
K
n
l’impresa non avrà
perdite in quanto l’area P0 ST R = K che è una misura dei costi fissi non recuperati con la parte
variabile della tariffa, sarà coperta dalla parte fissa della tariffa. I consumatori acquisteranno
la quantità q0 ed il loro surplus (non considerando la quota fissa) sarà maggiore del caso in
cui la tariffa applicata è quella lineare pari al costo medio.
Consideriamo il seguente esempio. La funzione di domanda è
Q = 1000 − 5p
ed una funzione di costo
C = 9000 + 100Q.
Allorché il prezzo è uguale al costo marginale il surplus del consumatore è 25000. Allorché
il prezzo è uguale al costo medio e non vi sono perdite, il surplus del consumatore è 14614.
Tale surplus è inferiore a quello che i consumatori sopporterebbero ripartendo la spesa di
9000, e ponendo un prezzo eguale al costo marginale. Ad esempio se i consumatori sono
100 e sono tutti eguali, una tariffa pari a 90 + 100Q permetterebbe di acquistare la quantità
corrispondente all’eguaglianza fra prezzo e costo marginale.
Nel caso in cui i consumatori abbiano domande dei beni non omogenee è possibile che un
consumatore esca dal mercato se il valore K/n è maggiore del surplus del consumatore allorchè
il prezzo è uguale al costo marginale.4
La soluzione efficiente è ottenuta se nessun consumatore è escluso dal mercato e tutti
pagano il costo marginale. Un’approssimazione della soluzione ideale può essere l’offerta di
un’alternativa di tariffe fra le quali i consumatori possono scegliere, del tipo indicato nella
abella 1.
Vediamo meglio le implicazioni di questa tariffa.
Consideriamo tre consumatori, uno per il quale il valore di 100 telefonate al mese è 16
euro, uno per il quale il valore di 200 telefonate è di 25 euro ed uno per il quale il valore di
300 telefonate è di 30 euro. Assumiamo che la funzione dei costi è C = 36 + 0, 05Q e quindi, la
4
Ciò può accadere per un servizio come quello telefonico, piuttosto che nel caso di servizi come elettricità,
acqua che sono beni di prima necessità.
21
spesa fissa da ripartire tra i tre consumatori è di 36 euro. Un’unica tariffa del tipo 12 + 0, 05Q
avrebbe l’effetto di far uscire il primo consumatore dal mercato in quanto spenderebbe per
100 telefonate 17 euro allorché il valore che egli attribuisce a 100 telefonate è di 16. L’impresa,
nel caso il primo consumatore uscisse dal mercato, non riuscirebbe a recuperare le spese in
quanto incasserebbe 49 mentre il suo costo sarebbe pari a 51. D’altronde il costo medio di
600 telefonate è 0,11. Se tale tariffa fosse applicata non converrebbe al terzo consumatore
fare 300 telefonate. Invece, il problema può essere risolto, offrendo una scelta fra le tariffe.
Si potrebbe ipotizzare che i consumatori con maggiore incentivo a pagare, paghino le spese
fisse in proporzioni maggiori in cambio di un minor prezzo per la telefonata. In tal modo, si
otterrebbe una soluzione più efficiente. Avremo, infatti, che tutti i consumatori stanno nel
mercato (il primo consumatore sceglierà la prima tariffa , il secondo la seconda, ed il terzo
consumatore la terza tariffa) e l’impresa recupera le spese fisse. Con la tariffa non lineare tutti
e tre i consumatori riescono a realizzare il numero desiderato di telefonate.
Table 1: Esempio di menu di tariffe non lineari
P. fissa
P. variabile
N. telefonate
Totale spesa
Spesa con
Surplus
tariffa 12+0,05q
5
l’impresa
6
0,09
Cons1 100
15
17
16
10
0,06
Cons2 200
22
22
25
20
0,03
Cons3 300
29
27
30
Tot 600
66
66
71
Tot 36
Costo per
66
È sempre necessaria la regolamentazione del Monopolio naturale?
Secondo la tradizionale teoria dell’interesse pubblico la regolamentazione pubblica dei settori
caratterizzati da monopolio naturale si rende necessaria per evitare che su tale mercato si
determinino prezzi monopolistici che non massimizzano il benessere sociale. Si sostiene infatti
che un monopolista tenderà a fissare il prezzo in base all’eguaglianza ricavo marginale-costo
22
marginale e il prezzo sarà posto ad un livello maggiore del costo medio di produzione. Si ritiene
che la regolamentazione possa migliorare il benessere del consumatore e l’efficienza economica
imponendo un prezzo eguale al costo medio di produzione.
D’altro canto abbiamo visto che sono necessarie notevoli informazioni per poter determinare una struttura di prezzi regolamentati che non si allontani di molto da quella ideale.
Inoltre i meccanismi attraverso cui si cerca di ottenere eguaglianza fra costo medio e prezzo (ad
esempio imponendo un vincolo sul tasso di rendimento) possono introdurre, come vedremo,
delle distorsioni nell’uso dei fattori di produzione e quindi determinare un uso non efficiente
delle risorse. La teoria della regolamentazione tradizionale è stata quindi sottoposta a numerose critiche e in numerosi paesi si è avuto un passaggio in molte industrie da un regime di
regolamentazione a uno di concorrenza.
Diviene quindi estremamente importante stabilire se una politica di non regolamentazione
può condurre a soluzioni ottimali dal punto di vista dell’allocazione delle risorse, anche se
la struttura industriale è dominata da una sola impresa. La teoria dei mercati contendibili
(Baumol, 1977) attraverso il concetto di configurazione sostenibile, cerca di individuare le
condizioni in cui non è necessaria la regolamentazione del monopolio naturale. Ricordiamo
che nel caso di impresa monoprodotto un monopolio naturale è detto sostenibile se esiste un
prezzo e una quantità tali che non vi è alcun incentivo a entrare da parte di nuove imprese, e se
a tale prezzo la domanda del mercato è interamente soddisfatta e i ricavi coprono i costi totali
di produzione. Una condizione sufficiente perchè il monopolio naturale sia sostenibile al prezzo
p uguale al costo medio è che la curva del costo medio sia decrescente e intersechi la curva di
domanda in corrispondenza di p e giaccia sopra la curva di domanda per ogni prezzo inferiore
a p (Figura 5). In questo caso non è necessaria una regolamentazione del monopolio naturale
e la condizione di libertà di entrata permette una soluzione che è socialmente desiderabile.
Vi sono altri casi in cui la libertà di entrata non è condizione sufficiente per eliminare
l’intervento dello Stato. È possibile, infatti, che proprio la libertà di entrata impedisca che
la produzione nell’industria sia realizzata in modo efficiente. Questo è il caso illustrato dalla
Figura 5.
Sia Y0 la quantità corrispondente al costo medio minimo; sia P0 il prezzo eguale al costo
medio minimo. Supponiamo che la domanda sia pari a Q(p) e sia p⋆ il prezzo determinato
dall’incontro della curva di domanda con la curva del costo medio. A tale prezzo il monopolista
23
Figure 5: Configurazione sostenibile in un mercato contendibile.
Figure 6: Configurazione non sostenibile in un mercato contendibile.
24
non realizza alcun profitto, e produce in modo efficiente in quanto non vi è altra configurazione
che permetta di produrre y ⋆ ad un costo inferiore. Questa configurazione non è sostenibile in
quanto è possibile l’entrata di un’altra impresa ad un prezzo compreso fra p⋆ e p0 . Un’impresa
che vende a un prezzo p′ leggermente inferiore a p⋆ e una quantità y ′ inferiore a y ⋆ , può realizzare un profitto positivo, e quindi la configurazione pur essendo efficiente non è sostenibile. Se
la nuova impresa non è obbligata a servire l’intero mercato, l’inesistenza di barriere all’entrata
determina un uso non efficiente delle risorse.
Questo mostra che anche quando sono soddisfatte le condizioni tecniche per l’esistenza
del monopolio naturale in una industria e non vi sono barriere all’entrata, è possibile che
il monopolio naturale non possa operare senza un intervento regolamentatore dello Stato.
Affinché non vi sia necessità di un intervento regolamentatore deve esistere un vettore dei
prezzi tale che non sia possibile l’ingresso profittevole nell’industria di nuove imprese allorché
tutta la domanda è soddisfatta e i ricavi coprono i costi di produzione.
Consideriamo l’esempio descritto da Faulkaber (1975).5 Vi sono tre imprese di gestione
dell’acqua e si supponga che un’impresa possa soddisfare il proprio mercato con un acquedotto
il cui costo è pari a $ 250.000, ma che due imprese possano operare insieme e gestire un unico
acquedotto per i propri mercati al prezzo di $ 300.000, e tre imprese insieme possano costruire
un acquedotto per i tre mercati al prezzo di $500.000. Il costo minimo per servire i tre mercati
è 500.000 dollari, ma due imprese hanno un incentivo a cooperare in quanto spenderebbero
solo $150.000 a testa, un costo inferiore a quello che risulta dalla cooperazione di tre imprese.
La terza impresa sarà svantaggiata se due imprese cooperano. È questo il caso in cui la libertà
d’ingresso non massimizza il benessere per la comunità.
5.1
Il caso di un’impresa multiprodotto
Abbiamo visto, nel caso di un’impresa monoprodotto, che la libertà di entrata non è condizione
sufficiente affinché il monopolio naturale possa operare senza un intervento regolatore dello
Stato. Solo se il prezzo è “sostenibile” dal monopolista non è necessaria la regolamentazione
pubblica. Discorso analogo vale per il caso di un mercato multiprodotto. Anche in tal caso
il problema è quello di vedere se esiste un vettore di prezzi che “sostiene” il monopolio nat5
G.R. Faulkaber, 1975, “Cross Subsidisation: Pricing in Public Enterprises”, American Economic Review,
n. 65, pp. 966-77.
25
urale. Prezzi sostenibili sono quelli che non incentivano l’entrata di imprese che utilizzano la
medesima tecnologia del monopolista, e nello stesso tempo non permettono al monopolista di
realizzare profitti superiori al normale.6
Le condizioni sufficienti a garantire la sostenibilità sono, nel caso di un mercato multiprodotto, notevolmente complesse e quindi è meno facile indicare i casi in cui l’intervento
regolamentatore dello Stato non è necessario. Occorre tenere conto che le possibilità di entrata sono molto maggiori che nel caso di un’impresa monoprodotto. Un concorrente può o
produrre l’intera gamma di prodotti o si può concentrare su un solo prodotto o può produrre
un numero più limitato di prodotti. Inoltre un’impresa che entra nel mercato può produrre,
in particolari mercati, una quantità maggiore di quella scelta dal monopolista.
La determinazione di prezzi sostenibili nel caso del monopolio naturale multiprodotto è
complicata dal fatto che i prodotti presenti nei vari mercati possono avere un certo grado di
sostituibilità. In tal caso l’entrata di un’impresa in un qualsivoglia mercato, se l’elasticità incrociata fra i beni è positiva, influirà sull’intera struttura della domanda. Inoltre la convenienza
all’entrata dipenderà dalle ipotesi che si possono fare sul comportamento del monopolista.
L’entrata di una nuova impresa può rendere non profittevoli per il monopolista, in relazione
alla quantità precedentemente prodotta o anche ad una quantità inferiore, i prezzi prevalenti in
caso di monopolio. In questo caso l’entrata sarà instabile e la soluzione che prevarrà dipenderà
dai comportamenti del monopolista e del concorrente.
Baumol, Willig e Panzar (1982) mostrano che affinché esista un vettore dei prezzi sostenibili
la funzione dei costi deve essere subadditiva. Ma questa condizione da sola non è sufficiente.
Nel caso di un’impresa multiprodotto i prodotti possono essere fra loro interdipendenti sia per
quanto riguarda il costo che la domanda. Giacché ogni prodotto ha un suo proprio prezzo,
alcuni prodotti possono essere venduti al di sotto del costo marginale e altri al di sopra, per
cui alcuni prodotti di un’impresa multiprodotto finanziano altri. Affinchè un vettore dei prezzi
sia sostenibile non deve esistere questo tipo di finanziamento incrociato; nessun prezzo deve
essere sussidiato. Un vettore dei prezzi è sostenibile se tutti i mercati sono in equilibrio, i ricavi
relativi agli n prodotti sono eguali ai costi di produzione totali, nessun prezzo è sussidiato e un
concorrente non ha alcun incentivo a produrre livelli produttivi, in ciascun mercato, inferiori
6
Per una discussione della teoria del monopolio naturale e della sua regolamentazione si veda W. W. Sharkey,
1982, The Theory of Natural Monopoly, Cambridge, University Press; R. Sherman, 1989, The Regulation of
Monopoly,The Regulation of Monopoly, Cambridge, University Press
26
quelli prodotti dal monopolista naturale. Sia la funzione di costo del monopolista C(q) e la
funzione di domanda Q(p) ove q e p sono rispettivamente vettori della produzione e dei prezzi.
Diciamo che il vettore dei prezzi p è sostenibile se:
1. qi = Di (p)
2. pq =
Pn
∀i = 1...n
i=1 Pi qi
= C(q)
3. pe q e < C(q e ) per tutti i pe ≤ p e q e ≤ Q(pe ), per i quali, allorché pei = pi , qie = 0, dove
l’apice e indica il vettore dei prezzi e delle quantità offerte da un nuovo entrante.
Baumol, Bailey e Willig (1977) dimostrano che i prezzi sostenibili sono anche prezzi ottimi di
second best, cioè prezzi Ramsey.
La principale conclusione che si può trarre dal risultato ottenuto da Baumol, Panzar e
Willig è che, in particolari condizioni, la libertà di entrata può obbligare il monopolista naturale
a scegliere prezzi socialmente desiderabili.
Questo non significa che la condizione di libertà di entrata sia condizione sufficiente per
eliminare l’attività di regolamentazione del monopolio naturale da parte dello Stato. Ad esempio, nel caso di costi fissi associati alle singole produzioni (invece di costi fissi comuni a tutte
le produzioni) la regola dei prezzi Ramsey comporterà che una produzione molto anelastica
dovrà sopportare una quota molto elevata di costi fissi, incentivando l’entrata di un concorrente che non deve rispettare la regola della massimizzazione del benessere collettivo. Quindi i
prezzi Ramsey non saranno sostenibili. D’altronde in presenza di elevati costi irreversibili non
sarà possibile seguire una politica di regolamentazione basata sulla concorrenza. In tal caso si
affiderà ad una sola impresa il servizio e un’agenzia dovrà controllare i risultati. In assenza di
concorrenza sarà difficile indurre un monopolista a seguire un comportamento che massimizzi
il benessere della collettività.
Non esiste dunque, da un punto di vista teorico, una politica ottimale nei confronti del
monopolio naturale valida in tutte le circostanze. Sarà solo l’analisi del caso singolo che permetterà di valutare se è più opportuno promuovere una politica di liberalizzazione all’entrata,
rischiando anche inefficienze derivanti da “fallimenti del mercato”, o attuare una politica di
regolamentazione senza libertà di entrata, che può determinare altri tipi di inefficienze.
27