Teorema del limite centrale TCL
Questo importante teorema della statistica inferenziale si applica a
qualsiasi variabile aleatoria che sia combinazione lineare di N variabili
aleatorie le cui funzioni di distribuzioni possono essere qualsiasi purché
abbiano valori attesi e varianze comparabili.
L’enunciato del teorema è il seguente:
Sia X una variabile casuale somma di variabili casuali xi
X = Σ a i xi
indipendenti ciascuna avente legge di distribuzione qualsiasi ma con
valori attesi comparabili e varianze finite dello stesso ordine di
grandezza.
la distribuzione di probabilità della variabile X tende, all’aumentare del
numero delle variabili aleatorie xi , alla distribuzione normale con
valore atteso E(X) = Σai E(xi)
e varianza
Var(X) = Σai2 Var(xi) .
Distribuzione di probabilità di
xmedio = Σxi/N
Un‘applicazione notevole del TLC è la determinazione della
distribuzione di probabilità della media campionaria
La media campionaria è una particolare combinazione lineare
xmedio = Σxi/N
delle misure xi che sono variabili aleatorie ripetute e
indipendenti proveniente da una stessa distribuzione che può
essere qualsiasi (uniforme, binomiale..) di cui si suppone
debba esistere valore atteso e varianza finiti (anche se non
noti).
TCL: Valor medio e varianza della
distribuzione delle medie
L’enunciato del TCL in questo caso si formula nel modo
seguente:
Sia dato un campione di N variabili casuali statisticamente
indipendenti tra loro e provenienti da una distribuzione di
probabilità ignota qualsiasi della quale esistono sia il valore medio
atteso che la varianza σ2 ( anche se non note)
Sotto queste condizioni la distribuzione delle medie campionarie
che si possono ottenere da un numero M di campioni della stessa v.a.
tende al crescere di N alla distribuzione normale con valor medio e
varianza (e quindi deviazione standard) dati dalle relazioni seguenti
Xmedio =
σ2medie = σ2/N
σmedie = σ /N
●
●
●
Naturalmente, il termine “grande” è relativo. Tanto più la
distribuzione della popolazione è diversa dalla normale,
tanto maggiore deve essere la dimensione N del campione
affinché sia sensato applicare il teorema del limite centrale.
La regola euristica è che un campione con N 30 sia
sufficientemente grande da giustificare l’applicazione del
teorema del limite centrale.
Un problema nasce quando la distribuzione della
popolazione è discreta. In questo caso, l’applicazione del
teorema porta ad approssimare la distribuzione discreta
con una distribuzione continua. Questo problema si risolve
introducendo quella che viene chiamata la “correzione di
continuita”
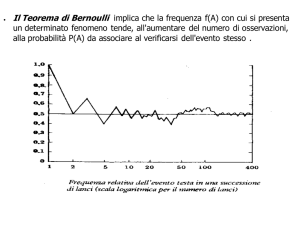
Gli studenti hanno già verificato nei risultati della loro esperienza
(lancio dei dadi) il significato della convergenza statistica della
media campionaria al valore atteso della popolazione da cui il
campione è estratto.
Nell’esempio qui riportato viene visualizzata la convergenza deli
valor medio di campioni di dimensioni N crescenti al valore atteso
= 10.5 della distribuzione di probabilità relativa alla comparsa di
una faccia di un dado equiprobabile di 20 facce.
Se non si conosce a priori la deviazione standard vera si usa la sua
miglior approssimazione x e la convergenza statistica stabilita dal
teorema del limite centrale si pone come
Questo importantissimo risultato verrà ottenuto anche in seguito
usando la propagazione degli errori (cap.8 del Cannelli)
Esso permette di calcolare deviazione standard delle medie dalla
deviazione standard delle singole misure;
Si osservi che la deviazione standard delle medie è 1/N volte più
piccolo della deviazione standard delle singole misure; questo implica
che le medie campionarie si distribuiscono intorno alla media delle
medie (che si suppone essere il valore vero ) con una curva di
distribuzione di Gauss la cui dev. standard è più stretta di quella della
distribuzione delle misure di un fattore 1/N
Convergenza delle distribuzioni Binomiale e di
Poisson alla distribuzione di Gauss
Una maniera alternativa per giustificare la convergenza delle
distribuzioni Binomiale e di Poisson alla distribuzione di Gauss
è basata sul Teorema del Limite Centrale.
Infatti la variabile k (Binomiale e di Poisson) può essere vista
come la somma di n variabili aleatorie, ciascuna delle quali
assume un valore 0 o 1 con probabilità p e q
k = i xi
xi = 0,1
Allora al crescere di n, la variabile aleatoria somma deve
presentare una distribuzione di probabilità che tende a quella
normale.