●
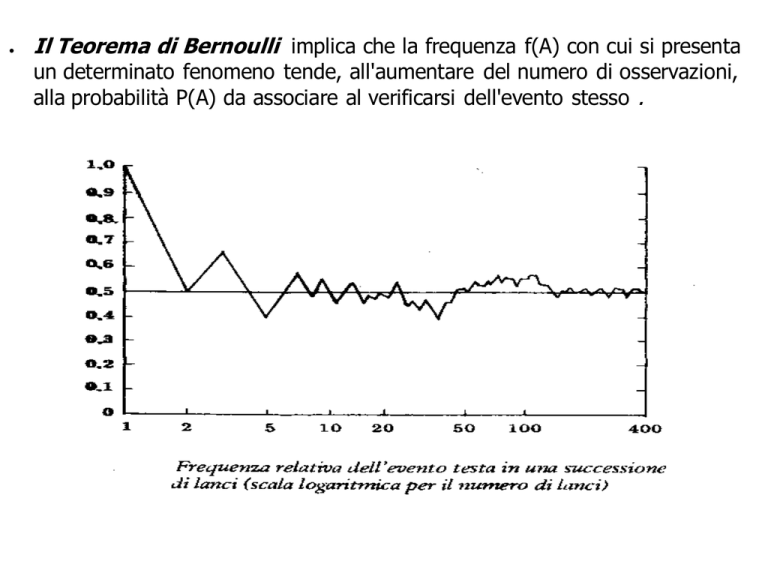
Il Teorema di Bernoulli implica che la frequenza f(A) con cui si presenta
un determinato fenomeno tende, all'aumentare del numero di osservazioni,
alla probabilità P(A) da associare al verificarsi dell'evento stesso .
La legge dei grandi numeri
●
La legge dei grandi numeri stabilisce invece una relazione tra la
media aritmetica xmedia di un certo campione (x1,x2,......,xN) di una v.a
(qualunque sia la sua distribuzione di probabilità ) e il valore
atteso E(x) di tale variabile.
●
Gli studenti hanno già verificato nei risultati della loro
esperienza (lancio dei dadi) il significato della convergenza
statistica della legge dei grandi numeri.
Esempio: Calcolo delle medie
Un dado a 6 facce viene lanciato 100 volte e raggruppando le
osservazioni in 10 set di 10 misure si è ottenuta la tabella seguente
osservazioni
●
●
con i 10 set di N=10 misure si osserva che i valori medi
fluttuano molto (da 2.9 a 4.1)
10 misure non sono sufficienti per avere un errore della
media accettabile (come verificheremo di seguito)
Calcolo delle deviazioni standard x
●
Calcoliamo per ogni set di N=10 osservazioni la deviazione standard
e confrontiamola con la deviazione standard per l’intero set di
osservazioni
●
-
-
osservazioni
con i 10 set di N=10 misure si osserva che i valori della
deviazione standard x hanno fluttuazioni molto inferiori
alle fluttuazioni dei valori medi (da 1.72 a 2.00)
il valore medio delle 10 x non coincide con il x
calcolato dalle 100 misure (l’operazione matematica del
calcolo di x non è lineare!)
Supponendo il dado equiprobabile si hanno valori di P(x) = 1/6
●
e il valore E(x) = x P(x) = 3.5 (indico con il valore E(x))
●
e il valore della Var(x) = (x - )2 P(x) =
●
= (x)2 P(x) - 2 x P(x) + ()2 P(x) =
●
=1/6*(1+4+9+16+25+36) - (3.5)2 =91/6-12.25=2.917
●
e quindi la σ = 1.708
Teorema del limite centrale: convergenza (per N
abbastanza grandi) della deviazione standard della
media
Xmedio a X/N
Consideriamo le 10 medie e calcoliamo la
deviazione standard delle medie xmedia
Usiamo la formula per N piccoli in cui le F i = 1
Dal confronto della Xmedia calcolata = 0.34
e i valori X/N
in tabella risulta che N=10 è ancora troppo piccolo per rendere
evidente la convergenza.












