Test dei punti di svolta/2

Componente erratica!
Le MM isolano la componente ciclica Ct della serie già detrendizzata e
destagionalizata. Ne consegue che i rapporti
(! C u $ +
et = 100 *# t t & '1)" C t % ,
Test dei punti di svolta!
Si conta il numero di svolte: picchi e valli.!
Una svolta richiede 3 punti consecutivi: et-1, et, et+1 . In una serie di n
punti esistono n-2 terne consecutive (esclusi il primo e lʼultimo)!
!
Dovrebbero avere natura essenzialmente erratica. Cioè
Se la serie fosse casuale allora i 3!=6 possibili ordinamenti sarebbero
equipresenti. Tra questi solo quattro contengono un punto di svolta!
A partire dalla variabile indicatore !
Turning points test!
Sono simmetrici intorno allo zero
Sono fra di loro incorrelati
"1 se et!1 <e t > et+1 oppure et!1 > e t < et+1
It = #
$0 altrimenti
Queste condizioni possono
essere sottoposte a verifica!
n"2
Sono privi di strutture riconoscibili
Il numero dei punti di svolta è!
P = # It
t= 2
Se non è così allora negli errori et è presente una componente sistematica che
non è stata ancora individuata dall’approccio classico.!
In caso di valori coincidenti il valore si considera unico e non ripetuto
riducendo conseguentemente n!
!
Test dei punti di svolta/2!
La statistica P ha valore atteso e varianza note!
n(2
n(2
"4% 2
E ( P ) = ) E ( It ) = )$ ' = ( n ( 2);
# & 3
t= 2
t= 2 6
16n ( 29
Var( P ) =
90
Allʼaumentare del numero dei termini, ferma restando la casualità, la
distribuzione di P tende alla gaussiana.!
!
Quindi possiamo testare lʼipotesi di residui senza struttura con la
statistica !
2
P " ( n " 2)
3
16n " 29
90
Se il valor p è inferiore a 0.01, si rifiuta lʼipotesi di erraticità!
!
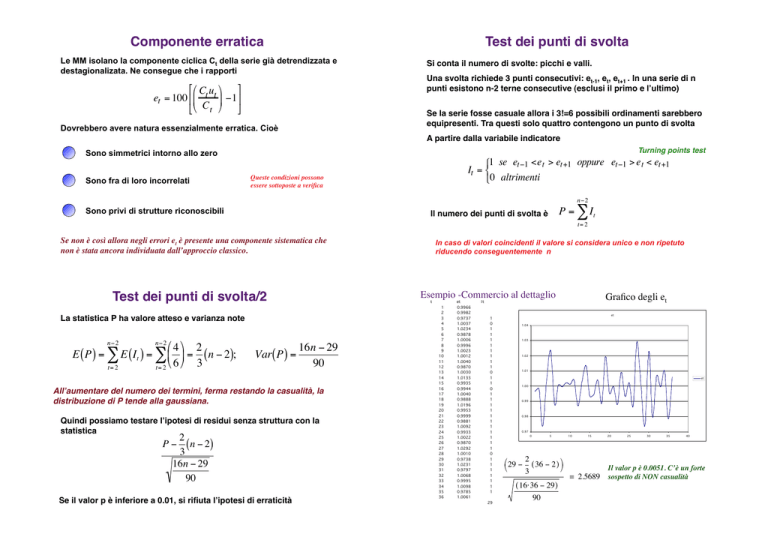
Esempio -Commercio al dettaglio!
t
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
et
0.9966
0.9982
0.9737
1.0037
1.0234
0.9878
1.0006
0.9996
1.0023
1.0012
1.0040
0.9870
1.0030
1.0133
0.9935
0.9944
1.0040
0.9888
1.0196
0.9953
0.9999
0.9881
1.0092
0.9933
1.0022
0.9870
1.0292
1.0010
0.9738
1.0231
0.9797
1.0068
0.9995
1.0098
0.9785
1.0061
Grafico degli et!
It
1
0
1
1
1
1
1
1
1
1
0
1
1
0
1
1
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
1
1
29
et
1.04
1.03
1.02
1.01
et
1.00
0.99
0.98
0.97
0
5
$ 29 ! 2 ( 36 ! 2 ) %
"
#
3
( 16& 36 ! 29 )
90
10
15
20
25
30
35
40
Il valor p è 0.0051. C’è un forte
= 2.5689 sospetto di NON casualità!
Test dei ranghi!
Test dei ranghi/2!
Il confronto può essere esteso a tutte le coppie di errori consecutivi.!
La q è legata al famoso ! di Kendall per
la correlazione tra ranghi !
!
!=
4q
"1
n( n "1)
Bisogna contare il numero q di volte in cui si ha ej>ei per j>i.!
!
! varia tra -1 e 1 ed ha valore atteso nullo in una serie erratica. !
Si considerano n(n-1)/2 coppie. Il valore atteso in una serie del tutto erratica è!
La deviazione standard del ! è!
E( q) =
n( n !1)
4
n ( n + 1)(2n + 5)
72
" (# ) =
Il rapporto tra ! ed il suo scarto quadratico medio può essere usato
per sottoporre a verifica lʼipotesi di erraticità!
!
318
4
"1
36x35
= 0.00026
36x37x77
72
Valori di q molto superiori alla media fanno pensare ad un trend crescente,
non del tutto rimosso dalla serie. !
Se invece q è molto minore della media il trend residuo deve essere ritenuto
decrescente. !
Commercio al dettaglio.!
Il valore del ! di Kendall è prossimo allo zero
per cui, almeno sotto questo aspetto della
casualità, è da ritenersi priva di struttura!
!
Test dei segni!
Test dei segni/2!
I segni degli errori si susseguono nel tempo in maniera casuale?!
!
Una coppia di segni successivi concordi: (+,+) oppure (-,-) è una
permanenza ed una di segni discordi (+,-) (-,+) è una variazione!
Ad esempio, la successione!
!
! + ! +
! + +
! ! + +
Segni
+
!
+
7
7
+ ! ! +
! ! + +
+ + !
! + +
Segni
+
!
Totale
+
7.28 5.72
13
!
6.72 5.28
12
Totale 14
11
25
Totale
13
12
!
6
5
Totale 14 11
!
!
Se la serie fosse casuale la tabella dovrebbe mostrare indipendenza!
25
A questo fine si può adoperare il test del chi-quadrato!
Valor p=0.8213!
Ha 25 coppie adiacenti di segni a partire da (-,-) e a finire con (+,+)!
Segni + ! Totale
+
7 6
13
!
7 5
12
Totale 14 11
25
! c2 =
Le permanenze sono 12 e riportate
sulla diagonale .!
!
Le divergenze sono 13 e riportate
fuori diagonale !
2
(7 " 7.28)
7.28
+
( 6" 5.72)
5.72
2
+
( 7" 6.72)
6.72
2
2
+
(5 " 5.28)
5.28
= 0.051
Se fosse vera lʼipotesi di casualità, un valore di chi2 pari a 0.051 o minore,
lo si potrebbe osservare lʼ82% delle volte (circa 8 su 10) cioè non è troppo
raro e quindi si accetta lʼipotesi che i residui siano casuali.!
t
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
et
-0.3400
-0.1784
-2.6325
0.3735
2.3406
-1.2167
0.0561
-0.0428
0.2343
0.1159
0.4016
-1.2977
0.2987
1.3346
-0.6549
-0.5628
0.3998
-1.1187
1.9568
-0.4661
-0.0104
-1.1868
0.9232
-0.6652
0.2222
-1.2964
2.9236
0.1017
-2.6192
2.3051
-2.0309
0.6815
-0.0458
0.9819
-2.1495
0.6148
--
++
1
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
5
+0
0
0
1
0
0
0
0
1
1
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
5
-+
0
0
0
0
1
0
1
0
0
0
1
0
0
1
0
0
1
0
1
0
0
0
1
0
1
0
0
1
0
1
0
1
0
1
12
0
0
1
0
0
1
0
1
0
0
0
1
0
0
0
1
0
1
0
0
0
1
0
1
0
1
0
0
1
0
1
0
1
0
12
Ricostruzione della serie storica !
Esempio :!
Commercio al dettaglio!
Si moltiplica il trend per i coefficienti di
stagionalità e di ciclicità!
Segni + ! Totale
+
5 12
17
!
12 5
17
Totale 17 17
34
Rt = Tˆt Cˆ t Sˆ t
! c2 = 5.765 " p # value = 0.0163
!
La casualità dei coefficienti di ciclicità è posta
seriamente in discussione da questo test!
Il Trend assorbe il movimento di lungo periodo, non ripetitivo, continuo e
senza sbalzi, almeno nellʼarco di tempo considerato.!
!
!
I coefficienti ciclicità esprimono oscillazioni periodiche pluriennali dovute a
cause congiunturali. !
!
!
La stagionalità rappresenta i movimenti legati a ricorrenze infrannuali
sistematiche ancorché irregolari che si esauriscono nellʼanno.!
Esempio !
Approccio classico e residui!
La serie ricostruita non ha componente erratica o almeno non la include
esplicitamente.!
!
Una stima approssimata degli errori si ottiene dalle relazioni!
Monthly Air traffic at Toulouse Blagnac Airport
0.00
-0.10
500
Residuals
0.10
Monthly Air traffic at Toulouse Blagnac Airport
2000
eˆt =
2005
2000
2005
0.4
0.2
PACF
0.0
!
-0.4
5
1995
Rt
Tˆ Cˆ Sˆ
"1 = t t t "1
Yt
Yt
Il successo del metodo di scomposizione si può misurare con il valor-p con
cui NON si rifiuta lʼipotesi di erraticità e, in misura minore, lʼipotesi di
gaussianità nei vari test proposti.!
-0.2
ACF
0.0
-0.4
-0.2
300
Passengers
Estimates
0.2
0.4
400
Passengers
1995
10
15
Lag
20
25
5
10
15
20
Lag
Inadeguatezza nella determinazione del ciclo-trend e, in misura minore,
nella stagionalità
25
Rispetto alla erraticità occorre considerare che, tanto i coefficienti di
stagionalità quanto quelli di ciclicità, provengono da medie mobili che
potrebbero aver indotto effetti di tipo Slustky-Yule.!
!
La presenza di strutture nei residui quindi non è necessariamente dovuta a
scelte sbagliate nella estrazione delle varie componenti.!
Gaussianità !
Verifica !
Consideriamo due indicazioni della gaussianità dei residui
Molta della teoria inferenziale delle
serie storiche poggia sull'ipotesi che i
residui siano gaussiani.
Bowman_Shenton (1975)
Ci si aspetta in pratica che se si
costruisse l'istogramma dei residui
esso assumerebbe la tipica forma
campanulare delle distribuzioni
gaussiane.
Nelle applicazioni della vita reale la
gaussianità è rara come l'unicorno e
quindi le indicazioni che la
presuppongono debbono sempre
essere valutate con sano scetticismo!
Quoziente logaritmico di variabilità
#" &
Log% e ( + 1
$ IQe '
Per residui gaussiani dovrebbero entrambi tendere a zero
!
Non discusse in
questo corso.
Esempio!
Esempio!
600
0.4
0.5
400
UK gas consumption
1965
1970
1975
1980
1985
E rimasta qualche componente
inespressa.
0.0
0.1
1960
0.2
U.S. dollars
Estimates
0.3
200
U.S. dollars
800
1000
1200
UK gas consumption
-4
-2
0
e
2
Esempio!
Altro esempio!
Le diagnostiche in questo caso
evidenziano un esito inadeguato.!
!
Le revisioni possono riguardare il Trend,
la Stagionalità ed il Ciclo.!
!
Per rrivare ad un buon risultato possono
essere necessari diversi passaggi.!
La ricostruzione è accettabile, ma è avvenuta conoscendo già quello che era
successo. Le previsioni sono un’altra cosa.!
Altro esempio/2!
Previsioni nellʼapproccio classico !
La estrapolazione delle componenti avviene con la traslazione temporale
delle formule!
Yˆt +k = Tt +k Ct +k St +k ; k = 1,2,...,
Allungare il trend è semplice: si valuta il modello analitico per le nuove
ascisse. Se non si allunga troppo, il risultato è in genere attendibile!
!
!
La stagionalità fissa o variabile si estende replicando i coefficienti dellʼultimo
anno.!
!
!
!
!
t+k
t+k"s
!
!
!
Anche la ciclicità si estende ipotizzando gli effetti del nuovo anno simili a
quelli del vecchio.!
!
S
Lʼapproccio classico sembra ignorare
informazioni significative sia rispetto al ciclotrend che rispetto alla stagionalità!
!
=S
; k = 1,2,...,
La previsione con l’approccio classico, nella versione da noi descritta, non può
prevedere l’intervento di eventi che modificano sostanzialmente il
comportamento della serie.!
!
Questi possono accadere anche nel brevissimo periodo!
Misure di adattamento!
http://camcomrer-test.redturtle.it/studi-ricerche/banchedati/bd/lavoro/amsocial/cig/cigordin/Cig_mensile.xls/view!
Il calcolo si basa sullʼidea del “leaving-one-year out”: un anno è accantonato
per valutare lʼaccuratezza della previsione.!
#
$ (Yˆ
Root Mean Squared Prediction Error!
t +k
RMSE =
" Yt +k ) /Yt +k
k=1
#
#
$ (Yˆ
t +k
Mean Absolute Prediction Error!!
#
$ (Yˆ
t +k
Theil' s U =
" Yt +k!
)
k=1
#
$ (Yˆ )
t +k
k=1
2
+
MAPE =
" Yt +k ) /Yt +k
k=1
#
2
(Yt +k )
2
I cambiamenti bruschi possono essere inclusi nel processo se sono già avvenuti
in passato.!
!
L’approccio classico non è esatto, ma può essere utile!
Lʼindice TU varia tra zero
ed uno!
2
ESEMPIO!
Le funzioni periodiche!
Ripasso !
Una funzione si dice periodica se i suoi valori si ripetono esattamente a
intervalli regolari.!
f ( t ) = f (t + kr)
Il seno di un angolo x (in gradi o radianti) è
definito a partire dalla circonferenza
goniometrica, ovvero dalla circonferenza
di raggio unitario nel piano cartesiano.!
" t, k = 0,±1,±2,…
!
Il minimo tra gli “r” che soddisfa tale condizione è il periodo della
funzione e questa è detta funzione periodica di periodo “r”!
Presa la semiretta uscente dall'origine che
forma un angolo x con l'asse delle ascisse,
il seno dell'angolo è il valore della
coordinata y del punto di intersezione tra
la semiretta e la circonferenza (in figura, è
la lunghezza del segmento DC).!
!
Le funzioni periodiche più comuni sono il seno e coseno trigonometrici.!
asen ( wt ), bsen ( wt )
con periodo:!
!
r=
2"
w
a e b sono dei coefficienti
Questa impostazione dellʼapproccio classico renderà più esplicite le
!
componenti periodiche quali la ciclicità e la stagionalità.!
!
Ripasso/2 !
Si definisce il coseno considerando una
circonferenza di raggio unitario ed una
semiretta uscente dall'origine che forma
un angolo x con l'asse delle ascisse.!
!
Il coseno dell'angolo x è definito come il
valore della coordinata x del punto di
intersezione tra la semiretta e la
circonferenza (lunghezza del segmento
OC).!
Funzioni seno e coseno!
La prima questione da affrontare è come si comporta la funzione sen
(ax) , dove a è un numero reale positivo fissato a piacere. !
!
Considerare “ax” come argomento del seno corrisponde a cambiare la
scala delle ascisse cioè il grafico di sen(ax) è quello di sen(x) ``dilatato''
o “contratto” secondo che “a” sia minore o maggiore di uno in valore
assoluto!
1.5
1
sen(x) nellʼintervallo (0,4π)
ha due picchi e due valli .!
sen(4x) ha 8 picchi e 8 valli!
Per angoli tra 0 e " / 2, il coseno
di un angolo è il seno dell'angolo
complementare, cioè!
sen(2x/π) sale e scende
una sola volta!
0.5
Sen(x)
Sen(4x)
0
0
-0.5
-1
-1.5
2
4
6
8
10
12
14
Sen(2x/π)
Seno e coseno/2!
Metodologia BV4!
Se le funzioni seno e coseno hanno periodo “r” allora saranno anche
periodiche con periodo “2r”, “3r”, …!
!
Quando si parla di periodo si sottintende che si considera il periodo
minimo, definito come il più piccolo p tale che f(x+r) = f(x) per ogni x!
!
Piú in generale sen(kx) e cos(kx) , con k intero, hanno come
periodo minimo r=2k/π.!
1.5
cos(x) nellʼintervallo (0,4π)
ha tre picchi e due valli.!
Studiamo una versione semplificata del metodo sviluppato dallʼufficio
centrale di statistica tedesco!
Si tratta di uno schema ADDITIVO!
yt = Tt + Ct + St + ut
Trend-Ciclo = Un polinomio in t (di solito la cubica)!
1
0.5
cos(4x) ha 9 picchi e 8 valli!
Cos(x)
Cos(4x)
0
cos(2x/π) sale una volta e
scende due volte!
0
2
4
6
8
10
12
14
Cos(2x/π)
Stagionalità = Somma di armoniche normalizzate!
-0.5
-1
Eʼ caratteristica lʼibridazione dei polinomi e delle armoniche di solito usate in
contesti diversi (ad esempio in fisica).!
-1.5
Scomposizione in serie di Fourier!
Scomposizione in serie di Fourier/2!
Questo approccio alle serie storiche venne avviato nei primi anni del secolo
scorso, ma ebbe sviluppo limitato a causa delle difficoltà di calcolo di quel
tempo.!
Lʼidea guida è che una funzione PERIODICA del tempo si possa esprimere
come una somma di termini trigonometrici (armoniche).!
m
) "i%
,
yt = / ai sen+ 2!$ ' t + ( i .
* # c&
i =1
#c periodicità massima
%2!i
%
c frequenza dell' armonica
$a ampiezza dell' armonica
%"i fase della armonica
% i
&m numero di armoniche considerate
m è da scegliere!
Lʼampiezza è lo scarto massimo (costante) di oscillazione rispetto allʼasse!
!
La fase è lʼascissa del primo punto di massimo.!
!
Il periodo esprime la durata dellʼoscillazione (curva tra due picchi)!
La frequenza (reciproco del periodo) si interpreta come il numero di
oscillazioni nellʼunità di tempo. !
!
ALTA FREQUENZA=MOLTE OSCILLAZIONI!
Stagionalità e funzioni trigonometriche!
La componente stagionale può essere espressa da una combinazione
lineare di “armoniche”:!
Stagionalità e funzioni trigonometriche/2!
La durata più breve in cui si può parlare di “ciclo” è 2 (da un dato a quello
successivo). Il massimo numero di armoniche stagionali è dato da!
"s
$ se s è pari
m = # 2s ! 1
$
; se s è dispari
% 2
m
St = ! ai sen( fi t + " i )
i è l indice della armonica!
i =1
Il coefficiente di stagionalità è la
St = coefficiente di stagionalità
somma delle armoniche.!
s = stagionalità (mesi ! s = 12)
2"i
fi =
frequenza della armonica
s
# i = fase della armonica
s = numero di periodi in cui si completa la stagionalità
i
m = numero massimo di armoniche in St
Questo è una tecnica di stagionalità variabile dato che il coefficiente varia
per lʼanno e per il periodo!
Infatti, in caso di “s” pari, la m-esima armonica completerebbe il suo ciclo !
in un numero di periodi uguale a:!
s s
= =2
m s
2
Dʼaltra parte non è necessario usare tutte le armoniche dato che le prime!
due o tre sono già in grado di esprimere complesse strutture ondulatorie.!
!
Le ultime armoniche sono poco oscillatorie e quindi poco utili.!
Stagionalità e funzioni trigonometriche/3!
Esempio di armonica!
a1 = 0; !1 = 0; a2 = "0.7; # 2 = 0.6944$ (125°)
Metodologia BV.4!
Se il trend è una polinomiale in “t”, il modello con stagionalità armonica è:!
k
m
y t = " 0 + # " i t k + # ai sen( f i t + $ i ) + ut
i=1
Stagionalità
1ª arm+2ª arm
j=1
il modello non è lineare a causa della presenza dei parametri " come!
argomento del seno. Tuttavia, tenuto conto che:!
!
!
!
!
!
La relazione può essere linearizzata:!
sen( x + y ) = sen( x ) *cos( y ) + sen( y ) *cos( x )
1ª armonica
k
m
y t = " 0 + # " i t + # a j [$ j1sen( f j t ) * cos(% j ) + $ j 2 cos( f j t ) * sen(% j )] + ut
!
k
2ª armonica
i=1
j=1
k
m
Gli angoli sono misurati in radianti!
[
]
= " 0 + # " i t + # & j1sen( f j t ) + & j 2 cos( f j t ) + ut
k
i=1
j=1
Ancora sulla BV.4!
Esempio!
Dato che la stagionalità deve compensarsi nellʼarco dellʼanno si pone il vincolo!
m
#" sen( f t ) + "
1i
i
2i
cos( f i t ) = 0 $
i=1
m&1
&# ["1i sen ( f i t ) + "2i cos( f i t )] & "1m sen ( f m t )
% 2m =
i=1
Scelta del trend e delle armoniche con la stepwise regression (si delega al
computer la selezione del numero di armoniche da usare)!
Che può essere soddisfatto
ignorando lʼarmonica m-esima
o una delle sue componenti
oppure togliendo lʼintercetta dal
trend-ciclo!
Ogni armonica è unʼonda
sinusoidale che completa il
suo ciclo ogni periodo.!
!
Le alte frequenze esprimono
variazioni di breve periodo
(stagionalità, settimane,
giorni).!
!
Le basse frequenze
esprimono componenti
cicliche con cadenze sempre
minori.!
cos( f m t )
30
!
25
Vendite mensile di auto nel Quebec-Canada!
20
"! %
fi = i $ ' , i = 1,2,…, 6
# 6&
15
10
5
0
Operatività!
Operatività/2!
I sottoperiodi si sovrappongono, almeno in parte.!
!
Ne consegue che per uno stesso periodo disponiamo di più stime!
È difficile che uno stesso modello rimanga valido per tutto lʼarco temporale.
Una validità per un periodo più ristretto sembra una strategia più realistica.!
!
La serie storica è quindi divisa in più sottoperiodi di numerosità simile h, ma
comunque superiore al numero di parametri da stimare !
Inizio
h > (k+1+s)!
h di solito è 4 o 3!
Se h=19 ed n= 34 allora le finestre di stima sarebbero!
i periodi indicati in colonna.!
!
Per ciascun sottoperiodo si devono stimare i parametri!
della cubica e delle armoniche. Per comodità i termini da
usare si scelgono con la stepwise regression.!
!
Invece di una media mobile abbiamo un modello mobile
che potrebbe essere diverso da periodo a periodo.!
!
Fine
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Inizio Fine
1
19
2
20
3
21
4
22
5
23
6
24
7
25
8
26
9
27
10
28
11
29
12
30
13
31
14
32
15
33
16
34
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Periodi di riferimento delle stime
5 6 7 8 9 10 11 12
6 7 8 9 10 11 12 13
7 8 9 10 11 12 13 14
8 9 10 11 12 13 14 15
9 10 11 12 13 14 15 16
10 11 12 13 14 15 16 17
11 12 13 14 15 16 17 18
12 13 14 15 16 17 18 19
13 14 15 16 17 18 19 20
14 15 16 17 18 19 20 21
15 16 17 18 19 20 21 22
16 17 18 19 20 21 22 23
17 18 19 20 21 22 23 24
18 19 20 21 22 23 24 25
19 20 21 22 23 24 25 26
20 21 22 23 24 25 26 27
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Ad esempio per il periodo 10 otteniamo il dato interpolato in 10
diverse situazioni (fino ad un massimo di 16). !
!
La sintesi dei valori stimati può farsi con la media, la mediana o altro.!
Applicazione alle vendite auto!
Applicazione alle vendite auto/2!
Trend cubico. Finestra=31. Metodo: weighted stepwise regression !
30
)
25
&
'
)
%
$
(
(
'
)&
%
20
(
&
%
#
'
$
(
)&
'
%
$
#
15
10
)
'
%
(
&
$
#
#
$
)
&
'
%
(
$
#
"
!
#
"
!
!
"
!
"
)
)
)
'
%
&
(
$
#
"
!
"
!
"
!
'
&
(
%
#
$
!
"
5
)
(
'
&
%
(&
'
%
$
#
"
!
!
1960
"
1961
#
1962
$
1963
%
1964
'
)&
(
$
&
&
1965
%
"
#
'
)
(
$
%
#
'
1966
(
1967
)
1968
!
$
"
!
#
"
!
Dicembre
Novembre
Ottobre
settembre
Agosto
Luglio
Giugno
Maggio
Aprile
Marzo
Febbraio
Gennaio
0
La stagionalità è presente ed in forma costante. Cʼè anche il trend.!
Cambio Euro/Dollaro Can.!
3.2
3.1
3.0
Monthly average
3.3
Exchange rate Euro/Can.$
2002
2003
2004
2005
2006
2007
2008
http://uif.bancaditalia.it/UICFEWebroot/cambiSSMForm.jsp?lingua=it!