Appunti di matematica
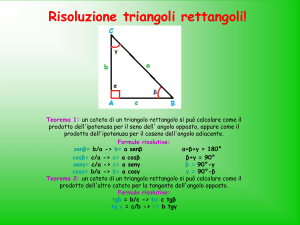
Risoluzione dei triangoli qualunque
Per risolvere un triangolo qualsiasi devono essere noti tre elementi di cui
almeno un lato.
Si possono presentare quattro casi:
1° caso - Noti due angoli e un lato.
Elementi noti: α, β , a
Elementi da trovare: γ, b, c
− Calcolo di
γ
L’angolo γ sarà:
γ = 180° − (α + β )
− Calcolo di b e c
b=a
Dal teorema dei seni si ricava:
senβ
senγ
, c=a
senα
senα
Esempio 1
Risolvere il triangolo qualunque ABC dati a=6 , α=45° e β =30°; trovare
γ, b, c.
− L’angolo γ sarà:
γ = 180° − (α + β ) ⇒ γ = 180° − (45° + 30°) = 180° − 75° = 105° ⇒ γ = 105°
1
senβ
sen30°
1 2
2
⇒b=6
= 6⋅ 2 = 6⋅ ⋅
= 6⋅
=3 2,
− Dalla formula b = a
senα
sen45°
2 2
2
2
2
b =3 2
2+ 6
senγ
sen105°
2+ 6 2
4
− Dalla formula c = a
⇒c=6
=6
= 63 ⋅
⋅
=
senα
sen45°
42
2
2
2
= 3⋅
2+ 6
= 3 1+ 3 , c = 3 1+ 3
2
(
)
(
)
prof.ssa Caterina Vespia
1
Appunti di matematica
2° caso - Noti due lati e l’angolo compreso.
b
Elementi noti: a, b, γ
γ
Elementi da trovare: α, β , c
a
− Calcolo di c
c = a 2 + b 2 − 2ab ⋅ cos γ
Dal teorema del coseno si ricava:
− Calcolo di
β
b
senβ = senγ da cui si ricava β.
c
Dal teorema dei seni si ha:
− Calcolo di α
L’angolo α sarà:
α = 180° − ( β + γ )
Esempio 2
6 − 2 , b = 2 e γ = 30° ;
Risolvere il triangolo qualunque ABC dati a =
trovare α,
β, c.
− Dalla formula c = a + b − 2ab ⋅ cos γ ⇒ c = a + b − 2ab ⋅ cos γ ⇒
2
c2 =
(
2
2
) ( )
6− 2 +
2
2
2 −2
(
(
6− 2
)
= 6−4 3 + 2 + 2− 2 2 3 −2 ⋅
c 2 = 4 − 2 3 ⇒ c = 4 − 12 =
− Dalla formula sen β =
)
2
2
2 ⋅ cos30° =
3
= = 10 − 4 3 − 6 + 2 3 = 4 − 2 3
2
4+ 4
4− 4
−
= 3 −1
2
2
b
sen γ ⇒ sen β =
c
2
sen 30° =
3 −1
2
(
)
3 +1 1
⋅ =
3 −1
2
6+ 2
4
⇒ β = 105°
− L’angolo α sarà: α = 180° − (γ + β ) ⇒ α = 180° − (30° + 105°) = 45° ⇒ α = 45°
prof.ssa Caterina Vespia
2
Appunti di matematica
3° caso - Noti i tre lati.
c
b
Elementi noti: a, b, c
Elementi da trovare: α, β , γ
a
− Calcolo di α
Dal teorema del coseno si ha:
− Calcolo di
γ
b2 + c2 − a2
cos α =
da cui si ricava α.
2bc
c
senγ = senα da cui si ricava γ.
a
Dal teorema dei seni si ha:
− Calcolo di β
L’angolo β sarà:
β = 180° − (α + γ )
Esempio 3
Risolvere il triangolo qualunque ABC dati a=2, b= 1 + 3 e c= 6 ; trovare α,β,γ.
2
2
(1 + 3) + ( 6 ) − 4 =
b2 + c 2 − a 2
− Dalla formula cos α =
⇒
2bc
2 (1 + 3 ) 6
=
=
1+ 3 + 2 3 + 6 - 4
2
(
6 +3 2
)
=
/2
/2
(
(
)
3 +3
6 +3 2
=
) (
(
) ( 6 − 3 2) =
2 )⋅ ( 6 − 3 2 )
3 +3 ⋅
6 +3
3 2 + 3 6 −9 2 − 3 6
−6 2
2
=
⇒ α = 45°
2 =
6 −18
2
−12
− Dalla formula senγ =
c
6
6 2 2 3
3
senα ⇒ senγ =
sen 45° =
⋅
= 2 =
⇒
a
2
2 2
4
2
γ = 60°
− L’angolo β sarà:
β = 180° − (α + γ ) = 180° − (45° + 60°) = 180° −105° = 75° ⇒ β = 75°
prof.ssa Caterina Vespia
3
Appunti di matematica
4° caso - Noti due lati e un angolo opposto ad uno di essi..
α
b
Elementi noti: a, b,α
Elementi da trovare: γ, β, c
a
Supposto α ≠ 90° e a ≠ b (altrimenti il triangolo sarebbe rispettivamente
rettangolo o isoscele e quindi facilmente risolvibile ), si ha:
− Calcolo di β
Dal teorema dei seni si ha:
b
a
b
=
⇒ senβ = senα da cui si ricava β.
a
senα senβ
1) Se senβ >1 ⇒ impossibile, perché -1<senβ <1
2) Se senβ ≤1 ⇒ si può ricavare β
In particolare:
− se senβ =1 ⇒ β=90° ⇒ se α>90°⇒ impossibile (perché α+β+γ=180°)
se α<90°⇒ 1 sola soluzione
− se 0<senβ<1 ⇒
se a>b ⇒ 1 soluzione
se a<b ⇒ se α≥90°⇒ impossibile
se α<90°⇒ 2 soluzioni β1 e β2
− Calcolo di
γ
L’angolo γ sarà:
γ = 180° − (α + β )
− Calcolo di c
Dal teorema dei seni si ha:
c
a
=
⇒
senγ senα
c=a
senγ
senα
Esempio 4
Risolvere il triangolo qualunque ABC dati a=12 , b=12 2 e α=30°; trovare c,
β, γ.
− Dalla formula
a
b
b
12 2
=
⇒ senβ = senα ⇒ senβ =
sen30° =
senα senβ
a
12
prof.ssa Caterina Vespia
4
Appunti di matematica
12 2 1
2
⋅ =
2
12 2
b
Poiché
senα <1 , a<b e α<90°⇒ 2 soluzioni β1 = 45° e β2 = 135°
a
=
− L’angolo γ sarà:
γ 1 = 180° − (α + β ) ⇒ γ = 180° − (45° + 30°) = 180° − 75° = 105° ⇒ γ 1 = 105°
γ 2 = 180° − (α + β ) ⇒ γ = 180° − (135° + 30°) = 180° −165° = 15° ⇒ γ 2 = 15°
− Dalla formula
c
b
=
⇒
senγ senβ
c=b
senγ
senβ
6+ 2
senγ 1
sen105°
4
1) c1 = b
⇒ c1 = 12 2 ⋅
= 12 2
=
senβ1
sen 45°
2
2
= 12
3
2⋅
6+ 2 2
⋅
=6
41
2
(
)
6 + 2 ⇒ c1 = 6 ( 6 + 2 )
6− 2
senγ 2
sen15°
4
2) c2 = b
⇒ c2 = 12 2 ⋅
= 12 2 ⋅
=
senβ 2
sen135°
2
2
= 12
3
2⋅
6− 2 2
⋅
= = 6 ( 6 − 2 ) ⇒ c2 = 6 ( 6 − 2 )
4
2
prof.ssa Caterina Vespia
5