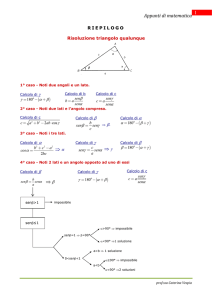
Appunti di matematica
Risoluzione dei triangoli rettangoli
Con l’espressione “risoluzione dei triangoli” si intende il calcolo degli elementi
di un triangolo, noti tre di essi, di cui almeno uno sia un lato.
1° caso - Noti i due cateti b e c determinare β, γ, a.
C
γ
a
α
β
B
b
c
A
− Calcolo di β
Dalla formula b = c ⋅ tg β si ottiene tg β =
− Calcolo di
γ
L’angolo γ sarà:
b
da cui si ricava β .
c
γ = 90° − β
− Calcolo di a
Dalla formula b = a ⋅ senβ si ricava:
a=
b
senβ
Esempio
Risolvere il triangolo rettangolo ABC sapendo che i cateti AC e AB misurano
rispettivamente 5 e 5 3 .
Dati b=5 e c=5 3 , trovare
β, γ, a
b
5
3
⇒ tg β =
=
si ricava β = 30° .
c
3
5 3
− L’angolo γ sarà: γ = 90° − β = 90°− 30° = 60°, γ = 60°
b
5
5
⇒a=
= = 10 , a = 10
− Dalla formula a =
senβ
sen30° 1
2
− Dalla formula tg β =
prof.ssa Caterina Vespia
1
Appunti di matematica
2° caso - Noti l’ipotenusa a e un cateto b, determinare c, β, γ.
C
γ
a
β
B
b
α
A
c
− Calcolo di β
Dalla formula b = a ⋅ senβ si ottiene senβ =
− Calcolo di
γ
L’angolo γ sarà:
b
da cui si ricava β .
a
γ = 90° − β
− Calcolo di c
Dalla formula c = a ⋅ senγ , si ricava c.
Esempio
Risolvere il triangolo rettangolo ABC sapendo che l’ipotenusa BC e il cateto AC
misurano rispettivamente 14 2 e 14.
Dati a= 14 2 e b=14, trovare
β, γ, c
b
14
2
⇒ senβ =
=
si ricava β = 45° .
a
2
14 2
− Dalla formula γ = 90° − β ⇒ γ = 90° − 45° = 45° , γ = 45°
− Dalla formula senβ =
− Dalla formula c = a ⋅ senγ ⇒ c = 14 2 ⋅ sen 45° = 14 2 ⋅
2
= 14 , c = 14
2
3° caso - Noti il cateto b e un angolo acuto β, determinare a, c, γ.
C
γ
a
α
β
B
b
A
c
− Calcolo di
γ
L’angolo γ sarà:
γ = 90° − β
prof.ssa Caterina Vespia
2
Appunti di matematica
− Calcolo di c
Dalla formula c = b ⋅ tgγ si ricava c.
− Calcolo di a
Dalla formula b = a ⋅ senβ si ricava:
a=
b
senβ
Esempio
Risolvere il triangolo rettangolo ABC sapendo che il cateto AC e l’angolo
misurano rispettivamente 21 e 60°.
Dati b=21 e
β
β =60°, trovare γ, a, c
− Dalla formula γ = 90° − β ⇒ γ = 90° − 60° = 30° , γ = 30°
21
21
b
2
=
= 21⋅
= 14 3, a = 14 3
⇒a=
senβ
sen60°
3
3
2
3
− Dalla formula c = b ⋅ tgγ ⇒ c = 21⋅ tg 30° = 21 ⋅
=7 3, c=7 3
3
− Dalla formula
a=
4° caso - Noti l’ipotenusa a e un angolo acuto β , determinare b, c, γ.
C
γ
a
α
β
B
b
A
c
− Calcolo di
γ
L’angolo γ sarà:
γ = 90° − β
− Calcolo di b
Dalla formula b = a ⋅ senβ si ricava b.
− Calcolo di c
Dalla formula c = a ⋅ cos β , si ricava c.
prof.ssa Caterina Vespia
3
Appunti di matematica
Esempio
Risolvere il triangolo rettangolo ABC sapendo che l’ipotenusa BC e l’angolo
β misurano rispettivamente 2 3 + 2 e 45°.
Dati a= 2 3 + 2 e
β =45°, trovare γ, b, c
− Dalla formula γ = 90° − β ⇒ γ = 90° − 45° = 45° , γ = 45°
2
=
2
= ( 3 + 1) 2 = 6 + 2 , b = 6 + 2
− Dalla formula b = a ⋅ senβ ⇒ b = (2 3 + 2) sen 45° = ( 2 3 + 2 )
− Dalla formula c = a ⋅ cos β ⇒ c = 2 3 + 2 ⋅ cos 45° = 2 3 + 2 ⋅
(
=
(
)
(
)
2
=
2
)
3 +1 ⋅ 2 = 6 + 2 , c = 6 + 2
prof.ssa Caterina Vespia
4