Risoluzione triangoli rettangoli!
Teorema 1: un cateto di un triangolo rettangolo si può calcolare come il
prodotto dell'ipotenusa per il seno dell' angolo opposto, oppure come il
prodotto dell'ipotenusa per il coseno dell'angolo adiacente.
Formule risolutive:
senβ= b/a -> b= a senβ
α+β+γ = 180°
cosβ= c/a -> c= a cosβ
β+γ = 90°
senγ= c/a -> c= a senγ
β = 90°-γ
cosγ= b/a -> b= a cosγ
γ = 90°-β
Teorema 2: un cateto di un triangolo rettangolo si può calcolare come il
prodotto dell'altro cateto per la tangente dell'angolo opposto.
Formule risolutive:
tgβ = b/c -> b= c tgβ
tg γ = c/b -> c= b tgγ
Formule risolutive...di un triangolo rettangolo!
teorema 1
senβ=
cosβ=
senγ=
cosγ=
b/a -> b= a senβ
c/a -> c= a cosβ
c/a -> c= a senγ
b/a -> b= a cosγ
teorema 2
tgβ = b/c -> b= c tgβ
tgγ = c/b -> c= b tgγ
α+β+γ=180°
β+γ = 90°
β= 90°-γ
γ= 90°-β
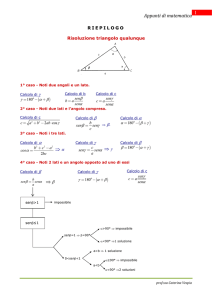
Risoluzione triangolo qualsiasi!
1. Teorema dei seni o di Eulero.
2. Teorema del coseno o di Carnot.
3. Teorema delle proiezioni.
Teorema dei seni o di Eulero...
Enunciato: I rapporti tra un lato e il seno dell'angolo opposto sono
uguali.
Formule:
a/senα = b/senβ = c/senγ
β= 180°-(α+γ)
a/senα = b/senβ
b= a senβ/senα
a/senα = c/senγ
c= b senγ/senβ
b/senβ = c/senγ
Teorema del coseno o di Carnot
Enunciato: Uno dei lati di un triangolo qualsiasi si puo calcolare
come la radice quadrata della somma dei quadrati degli altri due
lati meno il doppio prodotto degli altri due lati per il coseno
dell'angolo opposto.
Formule:
a = √ (b2+c2-2bc.cosα)
b = √ (a2+c2-2ac.cosβ)
c = √ (a2+b2-2ab.cosγ)
Teorema delle proiezioni
Enunciato: un lato di un triangolo qualsiasi e' uguale alla
somma dei prodotti degli altri due lati per il coseno
dell'angolo che questi due lati formano con il lato
considerato.
Formule:
AH= b.cosα
HB= a.cosβ
c= AH+HB = b.cosα + a.cosβ
a= b.cosγ + c.cosβ
b= a.cosγ + c.cosα