Rilassamento trasversale

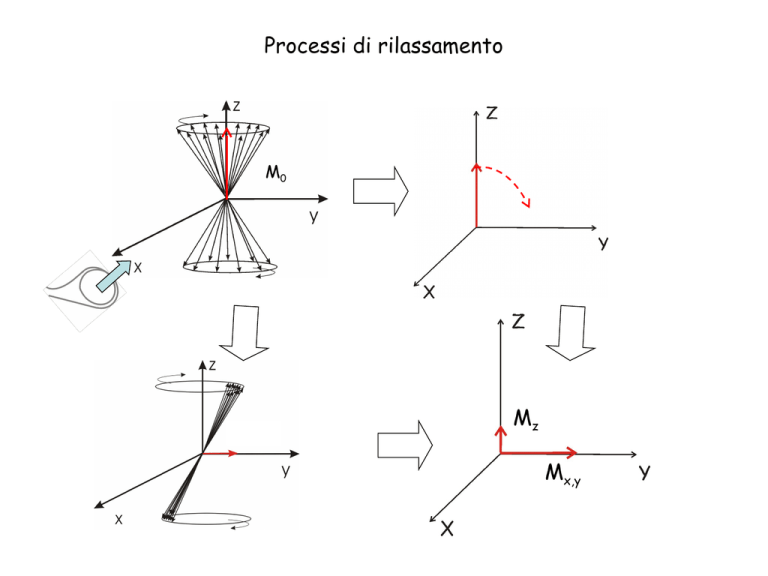
Processi di rilassamento
M0
Mz
Mx,y
Mz
Mx,y
Rilassamento trasversale
Rilassamento longitudinale
Spin-spin, adiabatico
Spin-reticolo, non adiabatico
dM z
M − M0
=− z
dt
T1
dM x ,y
Eqz. di Bloch
Mz(t)=M0+[Mz(0)-M0]*exp(-t/T1)
dt
=−
M x ,y
T2
Mx,y(t)=Mx,y(0)*exp(-t/T2)
T 2*
Perdita di coerenza
dovuta a
disomogeneità del
campo magnetico
T2
Spin-flip
Da dove arrivano le rf necessarie alle transizioni?
Uno spin risente di campi magnetici locali BL dati, ad es., da altri
spin presenti nelle vicinanze (interazione tra dipoli magnetici) …
… la cui intensità dipende
dall’orientazione della
molecola nel campo magnetico
Il moto molecolare rende
Bl oscillante nel tempo
Il rilassamento dipende
Dal fattore che genera il campo magnetico locale Bl
Dalla velocità del moto molecolare
Moti molecolari veloci
Densità
spettrale
Moti molecolari lenti
Densità
spettrale
Funzione densità spettrale J(ω)
τc
J (ϖ ) =
1 + ϖ 2τ c2
Tempo di correlazione
Densità spettrale in funzione di τc
J(ω ) =
τc
1 + ω 2τ c2
τc >
1
ω0
τc ~ 10-7 s
1
τc ≈
ϖ0
extreme narrowing
J (ϖ 0 ) ∝ τ c
τ c <<
1
ω0
τc ~ 10-12 s
Cosa succede in uno spettrometro 400 MHz invece che 100 MHz?
C’è differenza tra molecole “pesanti” (proteine ∼ kDa) e molecole leggere?
Densità spettrale  probabilità di transizione  velocità di rilassamento
Probabilità di transizione
Velocità di rilassamento
(Spin singolo)
R1 = 2W
Wα → β = Wβ →α = Bl2
R1 = 2 Bl2
τc
1 + ϖ 02τ c2
τc
1 +ϖ02τc2
-log R1
extreme narrowing
τ c <<
1
ϖ0
100 MHz
400 MHz
log(τc)
Dipendenza del tempo di rilassamento T1 dalla temperatura
logT1
log(τ
log(τcc))
Interazioni elettromagnetiche
Interazione con gli elettroni di legame (molecolari)
loc  indotto   
B = B0 + B
= B0 + δ ⋅ B0
Tensore di chemical shift
 Bxindotto   δ xx δ xy
 indotto  
 By
 =  δ yx δ yy
 B indotto   δ
 z
  zx δ zy
δ xz   0   δ xz B0 
   

δ yz  ⋅  0  =  δ yz B0 
δ zz   B0   δ zz B0 
Ri(c.s.a.) anisotropia del tensore di schermo
Interazione diretta tra dipoli magnetici (intra o intermolecolare)
Ri(d.d.) dipolo-dipolo
Interazione dipolare tra nuclei e elettroni spaiati
Ri(para) dipolare paramagnetica
Interazione con il gradiente di campo elettrico (per nuclei I > ½ )
Ri(q.) quadrupolare
Interazione con i campi magnetici generati dalla rotazione molecolare
Ri(s.r.) spin-rotazionale
Interazione per accoppiamento scalare
Ri(s.c.) scalar coupling
Ri = Ri(d.d.) + Ri(para) + Ri(q.) + Ri(s.r.) + Ri(c.s.a.) + Ri(s.c.)
Rilassamento per interazione dipolare
Wα → β = Wβ →α = Bl2
−
 µ0
γ Hγ H 3 
−
r 
 4π
τc
1 + ϖ 02τ c2
2
r
- Distanza internucleare 1/r6
- Rapporto giromagnetico dei nuclei che interagiscono
Variazione di T1 in seguito a sostituzione isotopica 
misura delle distanze interatomiche
Rilassamento per anisotropia di Chemical shift
Wβ →α = Wα → β = B2x
τc
1 + ϖ 02τ c2
( γ B0 ∆σ ) 2
∆σ = σ zz − 12 (σ yy + σ xx )
-13CH3
sp3
∆σ = 35 ppm
-13C=CH2
sp2
∆σ = 189 ppm
-13C CH
sp
∆σ = 230 ppm
-13C N
sp
∆σ = 316 ppm
C
13
Anisotropia del tensore di schermo
Intensità del campo magnetico
C: T1
13
OH
Qual è il meccanismo di rilassamento
principale per ciascuno dei 13C della molecola
di L-DOPA?
HO
NH2
CH2 C
COOH
H
1.5
0.25
0.25
0.5
HO
0.27
1.5
0.34
1.5
0.51
0.26
0.31
0.44
0.67
0.49
0.42
2.0
1.8
2.1
Della molecola di colesterolo confontare i
13
C-T1 della parte ciclica con quelli della
catena alifatica: c’è una spiegazione per le
differenze osservate?
Rilassamento di due spin accoppiati dipolo-dipolo
Cross-relaxation e T2
W+-=W -+ = transizioni a quanto nullo
W++=W -- = transizioni a doppio quanto
Probabilità di transizione W0, W1 e W2 e densità spettrali
W1 =
3
Bl2 J (ϖH )
20
W2 =
3
Bl2 J ( 2ϖH )
5
W0 =
1
Bl2 J ( 0 )
10
Velocità di rilassamento longitudinale (spin reticolo) T1
e trasversale (spin-spin) T2 in funzione di W0, W1, W2
Teoria Bloembergen-Purcell-Pound (BPP)
R1 = 2W1 + 2W2
2
3 µ
=
R1 =  − 0 γ 2 3  { J (ϖ H ) + 4J( 2ϖ H )}
10  4π
r 
R2 = 3W0 + 5W1 + 2W2
2
3  µ0 2 = 
R2 =
γ 3  { 3J ( 0 ) + 5J (ϖ H ) + 2J( 2ϖ H )}
−
20  4π
r 
W2 >> W1
W0 >> W1 > W2
T1
W2 ≅ W1
Extreme
narrowing limit
T2
τc << 1/ωH
W2 >> W1
R1 , R 2 ∝
τc
r6
τc
W0 >> W2 ≅ W1
Effetto nucleare Overhauser: positivo o negativo?
η = 1+
W2 − W0
W0 + 2W1 + W2
Probabilità di cross-relaxation
Probabilità di transizione totale
Perché l’effetto Overhauser 1H-13C è sempre positivo?
1
H-13C
ωC
ωH−ωC ωH
2
1 µ
=
W0 =  0 γ Hγ C 3  J ( ωH − ωC )
10  4π
r 
ωH+ωC
2
3 µ
=
W2 =  0 γ Hγ C 3  J ( ωH + ωC )
5  4π
r 
nOe eteronucleare
ηC = 1 +
W2 − W0
γH
γ C W0 + 2W1 + W2
C
13
N
15
Misura del T1: sequenza di Invertion Recovery
ττ τintermedio
corto
lungo
(
M z ( t ) = − M 0 1 − 2e
−
t
T1
)
 M − M z (τ ) 
τ
ln  0
=
−

2
M
T1
0


13
C-NMR
T1≅
τ(M =0)/ln2
z
T1(CH3) = 7.20s
T1(CH2) = 14.40s
T1(C2) ≅ T1(C3) ≅ T1(C4)= 17.31s
T1(C1)= 72.13 s
Rilassamento trasversale
(spin spin)
dM y
dt
=−
My
T2
dM x
M
=− x
dt
T2
ln M y ( t ) = ln M 0 −
t
T2
T2 tempo di rilassamento trasversale
T2 ≤ T1
Misura del T2*: larghezza del segnale
T2* =
1
T2*
=
1
∆ν
1
2
1
1
1
+
=
+ γ∆B0
T2 Tdisomog T2
Disomogeneità di
campo magnetico
Disomogeneità
del campione
Misura del T2: sequenza spin-eco
90°
τ
180°
τ
Eco di spin
dM x ,y
dt
=−
M x ,y
T2
 τ 

M x ,y (τ ) = M 0 exp  −

T
2

Mx,y
τ