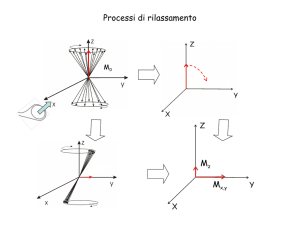
NMR Stato Solido
Non distruttivo
Studio di materiali
Solidi cristallini, amorfi, polveri
Polimeri insolubili, membrane cellulari, materiali ceramici, legno, ossa
Non richiede preparazione del campione, posso analizzare miscele senza
separarle
Studio di conformazioni e moti molecolari allo stato solido
Alta concentrazione del campione spettri 13C e 31 P
Energia di uno spin nucleare in un campo magnetico B0
H = HZ + HD + Hcsa + HJ + HQ
HZ = Interazione di Zeeman (con B0)
HD = interazione dipolare
Hcsa = interazione con la nube elettronica (determina il chemical shift)
HJ = accoppiamento scalare (attraverso gli elettroni di legame)
HQ = Interazione quadrupolare
tutte le interazioni sono tensori
(dipendono dall’orientazione)
In soluzione
Moto molecolare
isotropo
Tensore mediato a un
singolo valore isotropo
Linee strette
SSNMR
(Solid State)
La natura tensoriale
delle interazioni si
mantiene
δ
δ xy
xx
δ = δ yx δ yy
δ
zx δ zy
δ xz
δ yz
δ zz
Linee larghe
Anisotropia del tensore di schermo (csa)
C-NMR
13
Cristallo singolo
Spettro di polveri
In soluzione
O
O
+
H C Ca
C
O
O
B0
H
H
C
O
O
O
+
Ca
O
C
H
Anisotropia del tensore di schermo componenti principali
Facendo ruotare
il cristallo lungo
ciascuno dei tre
assi
H
z
C
O
O
Ca+
O
O
C
y
x
H
In soluzione
range di c.s.
fattore di anisotropia
Anisotropia di chemical shift
δzz
δxx
δyy
tensore di schermo
tensore di chemical
shift
δxx=234 ppm
δ11 > δ22 > δ33
δyy=189ppm δzz=104 ppm
Lo spettro si estende in un
range di 130 ppm!
δiso= 1/3 (δ11 + δ22 + δ33)
δ= 172 ppm
Spettro di polveri
δiso < δ22
Spettro di un cristallo singolo
σiso>σ22
σ22
k=0.13
8 diverse forme ioniche in una cella
elementare
Tensore di csa assiale
ellissoide oblato
ellissoide prolato
benzene
acetilene
σ||
σ⊥
σ11 = σ||
σ22 = σ33 = σ⊥
σ⊥ > σ ||
σ⊥
σ||
σ11 = σ22 = σ⊥
σ⊥ < σ ||
σ33 = σ||
Moto molecolare isotropo allo stato solido chemical shift isotropo
C alifatici: σ11 = 98 ppm; σ22 = 106 ppm; σ33= 123 ppm
13
σiso= 109, k = 0.14
adamantano
Accoppiamento dipolare
E dd = −
µ 0 γ k γ jµ 1
(
3 cos 2 θ − 1)
3
2π r 2
Per quale orientazione l’accoppiamento dipolare è massimo?
Per quale valore di θ l’interazione dipolare è nulla?
Calcolare l’energia di interazione massima tra due protoni alla distanza r = 5*10-10
θ = 0°
θ = 90°
(3 cos
2
∆ν = -12 KHz
∆ν = 6 KHz
θ − 1) = 0
∆νmax = -12 KHz !!
cos θ =
1
3
θ
= 54.74°
> dell’intero range di chemical shift del 1H
energia delle interazioni
c.s.a. ≅ 1*104 Hz
Accoppiamento d.d. ≅ 1*105 Hz
J coupling ≅ 1*102 Hz
Come mediare al valore isotropo i valori anisotropi?
Rotazione attorno all’asse θ
(diagonale di un cubo)
Valore mediato a σiso
Rotazione attorno a un asse (x,y o z)
valore mediato σxx σyy σzz
Angolo magico
(3cosθ
2
-1)=0
La velocità di spinning deve essere > dell’anisotropia da mediare
Un segnale 13C ha un’anisotropia di 400 ppm a quale velocità (in Hz) deve
essere fatto ruotare il campione su uno strumento 100 MHz?
10000Hz
δiso:
non cambia al
variare della velocità
di spinning
Spinning side bands ∆SSB= velocità di rotazione
CH3
H3C
CH3
H3C
CH3
CH3
Interazione dipolare 1H-13C
∆ν = −
o
∆νmax = 47 KHz !!
r1H −13C = 1 A
13
O
H3C
µ 0 γ Hγ C ν 1
(
3 cos 2 θ − 1)
3
2π r
2
C NMR of alanine in solution
OH
NH2
spinning (5 kHz)
accoppiamento dipolare e csa
Come eliminare l’accoppiamento dipolare
Caso eteronucleare disaccoppiamento ad alta potenza
con disaccoppiamento 1H
O
H3C
OH
NH2
–
disaccoppiamento 1H + MAS
CO2
CH3
CH
*
*
Accoppiamento dipolare 1H-1H ≅ 1*105 Hz
Sequenze di impulso
T1 e T2 nello stato solido
rilassamento traversale molto veloce
rilassamento longitudinale molto lento
FID decade rapidamente
Tempi di accumulazione 13C nei solidi >> tempi di accumulazione in soluzione
Rilassamento longitudinale e trasversale e campi magnetici locali
Energia di interazione tra magnetizzazione M e campo
magnetico applicato B
E = −M ⋅ B = − MB cos θ
Solo le componenti ⊥ alla magnetizzazione contribuiscono al suo rilassamento
Rilassamento longitudinale
Spin-reticolo
Rilassamento trasversale
Spin-spin
Cross-polarization
Spin lock
x
B1
z
z
M0
M0
y
(90°)x
x
B1
y
(rf)y
Locked magnetization
La locked magnetization non decade per T2 (è costretta a rimanere lungo y); al
rilassamento longitudinale (T1, spin reticolo) della locked magnetization
contribuiscono oscillazioni lungo il campo magnetico principale la
magnetizzazione è forzata a scambiare energia con il reticolo
Temperatura di spin
1
H: spin “freddi”
Hartmann-Hahn
matching
C:
spin “caldi”
13
reticolo
Spin freddi: magnetizzazione elevata intenso scambio con il reticolo
Spin caldi: magnetizzazione bassa poco scambio con il reticolo
Condizione di “contatto” Hartmann-Hahn ωH=ωC
γHB1(H)=γ CB1(C)
“Raffreddamento” degli spin “caldi” (e viceversa)
Durante il Contact time le ω di 1H e 13C sono rese uguali, le due specie atomiche
precedono nel sistema di riferimento ruotante alla stessa frequenza se sono
soddisfatte le condizioni di Hartmann Hahn
γ 13C B1(13C ) = γ 1H B1(1H )
Incremento del segnale 13C = γH / γ13C
T1 del 1H