Economia Politica 2 - MICROECONOMIA
ESERCITAZIONE 1
Testi esercitazione 3 Ottobre 2002
SOLUZIONI
ESERCIZIO 1
(Prova di Economia Politica II del 10 luglio 2002, Parte 2, Domanda 1)
Le preferenze di un consumatore sono espresse dalla funzione di utilità U (x,y) = xy.
1) Determinare l’insieme dei panieri che risultano indifferenti al paniere w (3,4) e poi si
rappresenti graficamente la curva di indifferenza passante per w.
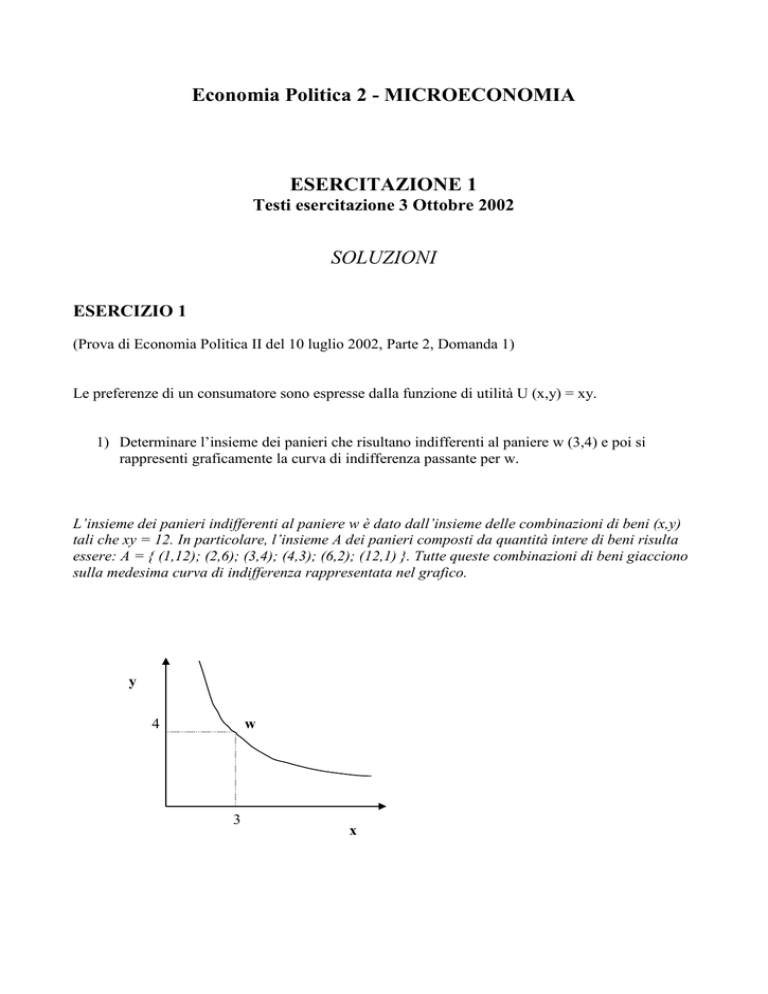
L’insieme dei panieri indifferenti al paniere w è dato dall’insieme delle combinazioni di beni (x,y)
tali che xy = 12. In particolare, l’insieme A dei panieri composti da quantità intere di beni risulta
essere: A = { (1,12); (2,6); (3,4); (4,3); (6,2); (12,1) }. Tutte queste combinazioni di beni giacciono
sulla medesima curva di indifferenza rappresentata nel grafico.
y
4
w
3
x
2) Posto che l’insieme ammissibile di scelta sia costituito dai seguenti panieri: w1 (3,4);
w2 (7,9); w3 (5,6); w4 (2,1); w5 (3,2), stabilire l’ordinamento delle preferenze.
U ( w1 ) = 12; U ( w2 ) = 63; U ( w3 ) = 30; U ( w4 ) = 2; U ( w5 ) = 6.
L’ordinamento delle preferenze risulta essere: w2 > w3 > w1 > w5 > w4
dove il simbolo > sta per “preferito a”.
Graficamente abbiamo che w2 giace su una curva di indifferenza più a NE rispetto a w3 , che a sua volta
appartiene ad una curva più esterna rispetto a w1 e così via.
3) Determinare la scelta ottima del consumatore supponendo che il reddito sia M = 5, il prezzo
del bene x sia px = 2 ed il prezzo del bene y sia py =3.
Nell’espressione generica del vincolo di bilancio ( pxx + pyy = M ) sostituiamo gli specifici valori
dei prezzi e del reddito.
Otteniamo così il vincolo di bilancio in forma implicita: 2x+3y = 5.
Riscriviamo il vincolo in forma esplicita in modo da evidenziare pendenza (-2/3) ed intercetta
verticale (+5/3): y = -2/3x +5/3.
Impostiamo quindi il sistema per la determinazione della scelta ottima:
Px
y 2
MRS
Py
x 3
V .diB.
y - 2/3x 5/3
Risolvendo per y la prima equazione e sostituendo nella seconda otteniamo il seguente paniere di
scelta ottima E(5/4; 5/6).
Graficamente:
y
E
●
5/6
5/4
x
ESERCIZIO 2
(Prova di Economia Politica II del 12 Settembre 2002, Parte 2, Domanda 1)
Data la funzione di utilità U (x,y) = xy + 3x + 6y
con reddito del consumatore pari a m=200, prezzo del bene x pari a px = 4 e prezzo del bene y pari a
py =2, calcolare:
a) La scelta ottima.
P
y3 4
y 2x 9
y 54,5
MRS X
x 6 2
PY
200 4 x 4 x 18 x 22,75
200 4 x 2 y
VincoloBil ancio
b) Il valore dell’utilità nel punto di scelta ottima.
Il valore della funzione di utilità nel punto E (22,75;54,5) è dato da:
U(E) = 22,75*54,5+3*22,75+6*54,5 = 1635,125
c) La scelta ottima se il reddito diventa 220.
Procedo in modo analogo al punto a, inserendo nel sistema il vincolo di bilancio col reddito
variato ed ottengo il paniere E’ (25,25;59,5)
d) Il valore dell’utilità nel punto di scelta ottima con reddito pari a 220.
In modo analogo al punto b, calcolo anche U(E’)= 1935,125.
ESERCIZIO 3
(Prova di Economia Politica II del 30 gennaio 2002, parte II, Domanda 1)
Consideriamo 2 beni, x ed y. Siano i rispettivi prezzi pari a px=2 e py=4:
e) Tracciare in un riferimento cartesiano il vincolo di bilancio di un consumatore il cui reddito
è pari a m=100; indicare le intercette ed il valore del coefficiente angolare.
Ricordando che l’equazione generica del vincolo di bilancio (in forma implicita) è la seguente:
px* x + py * y = m
sostituiamo il valore dei prezzi e del reddito:
2x + 4y = 100
Per disegnarlo, ne ricaviamo la forma esplicitando rispetto ad y:
y = (- 1/2) x + 25
Coefficiente angolare:
Intercetta verticale:
Intercetta orizzontale:
- 1/2
x = 0 y = 25
y = 0 x = 50
Rappresentazione grafica:
y
25
coeff. ang = - 1/2
O
50
x
f) Come si modifica il vincolo di bilancio se il prezzo del bene y varia da 4 a 8?
py aumenta, quindi il rapporto px / py (che rappresenta l’inclinazione del vincolo di bilancio)
diminuisce ( passa da ½ a ¼): il vincolo diventa meno inclinato e ruota intorno all’intercetta
orizzontale che rimane invariata, a differenza dell’intercetta verticale che diventa 25/2.
Rappresentazione grafica:
y
25
25/2
coeff. ang = - 1/4
O
50
x
g) Come si modifica il vincolo di bilancio se i prezzi dei due beni raddoppiano?
In questo caso, il rapporto tra i prezzi dei due beni non cambia, quindi il vincolo di bilancio
mantiene la stessa inclinazione iniziale; tuttavia, essendo m fisso, i beni possono essere
consumati nella stessa proporzione ma in quantità minore: il vincolo si sposta parallelamente
verso l’origine.
Rappresentazione grafica:
y
25
25/2
coeff. ang = - 1/2
O
25
50
x
I beni x e y sono perfetti sostituti: la funzione di utilità è la seguente: U x, y 3x y
h) Disegnare la mappa della curve di indifferenza.
Riscriviamo la funzione di utilità in forma esplicita:
y = U – 3x
e disegnamo la mappa di curve di indifferenza assegnando valori arbitrari ad U.
Rappresentazione grafica:
y
inclinazione delle curve
di indifferenza = - 3
O
x
i) Se px=2, py=4, m=100 individuare la scelta ottima.
Calcoliamo il saggio marginale di sostituzione tra i due beni:
U
MU x x
MRS
3
MU y U
y
Nel caso dei perfetti sostituti, troviamo la scelta ottima confrontando il MRS con il rapporto tra
i prezzi.
Essendo MRS > px / py (perché 3 > ½ !), tutto il reddito viene speso nel consumo del bene x. La
scelta ottima sarà quindi (50, 0)
j) Rappresentare graficamente la scelta ottima.
Rappresentazione grafica:
y
O
50
x
ESERCIZIO 4
La funzione di utilità di Gaia, volenterosa studentessa di microeconomia, è U(x,y) = x 2y, dove x
indica numero di eserciziari e y numero di penne a sfera. I prezzi di questi due beni sono,
rispettivamente, px = 1 e py = 3, mentre il reddito che Gaia vuole destinare quel mese ad eserciziari
e penne a sfera è I = 180.
a) Scrivete il vincolo di bilancio di Gaia e rappresentatelo nel grafico sottostante.
I px x p y y
180 x 3 y y 60 1 3x
Y
60
20
180
120
X
b) Calcolate il saggio marginale di sostituzione fra i due beni
MRS
U x MU x
y
2
U y MU y
x
c) Calcolate quanti eserciziari e quante penne a sfera Gaia consumerà quel mese e rappresentate il
paniere d’equilibrio nel grafico precedente.
x
y
2 y 1
6
x 3
x
180 x 3 y 180 x
x
2
y
x
6
120
y
20
6
2
180 120 x 120
3
d) Derivate la funzione di domanda per entrambi i beni.
Procediamo con la derivazione della domanda relativa agli eserciziari, lasciando nel
precedente sistema implicito il prezzo del bene (px):
2 y px
x
3
180 px x 3 y
px x
px x
y
p
x
y
y x
6
6
6
120
px
180 px x x
3 / 2 px x 180 x
px
2
In modo analogo, lasciando stavolta implicito py, ricaviamo la funzione di domanda perle
penne a sfera:
x
x 2 yp y
1
2y
x 2 yp y
2y
60
py
x
py
3 p y y 180; y
2
yp
p
y
180
y
y
180 x p y y 180 x p y y
py
e) Calcolate la spesa complessiva in ciascuno dei due beni.
px x 1 120 120;
p y y 3 20 60
f) Ipotizzando che il prezzo degli eserciziari raddoppi (px = 2) come varierà la spesa
complessiva in penne a sfera?
x
x
60
y
2 y 2
y
y
20
3
x 3
3
3
180
180 2 x 3 y 180 2 x x x
60 x 60
3
La spesa totale in y rimane invariata 60
ESERCIZIO 5
Si consideri un consumatore che deve scegliere la quantità del bene x e del bene y da consumare. La
sua funzione di utilità è U(X,Y) = 2x + 2y, i prezzi sono rispettivamente P x =1, Py = 3 e il reddito
M = 9.
1) Si scriva il vincolo di bilancio del consumatore e lo si rappresenti graficamente, indicando il
valore delle intercette e dell’inclinazione.
x + 3y = 9
Intercette: (0,3) e (9,0); pendenza –1/3
Y
E2
V.
B.
(0,3)
E1
(9,0)
X
2) Di che genere di beni si tratta?
Di beni perfetti sostituti
3) Si rappresentino graficamente almeno 3 curve di indifferenza.
(Linee tratteggiate nel grafico)
4) Quale sarà il punto di equilibrio?
E’ una soluzione d’angolo: poiché il vincolo di bilancio è meno pendente delle curve di indifferenza
(MRS> Px / Py) , il consumatore acquisterà solo 9 unità del bene x.
5) Si ipotizzi che il prezzo del bene x passi da Px =1 a P’x = 4. Come varierà il punto di equilibrio.
La pendenza del vincolo di bilancio diventerà maggiore di quella delle curve di indifferenza (MRS<
Px / Py) e quindi il consumatore acquisterà solo 3 unità del bene y.
Esercizio 6
La funzione di utilità di Aldo è data da U(x,y) = x2 y2 dove x rappresenta lo yogurt e y la frutta. I
prezzi di questi due beni sono rispettivamente: px =2, py=5 mentre il reddito a disposizione di Aldo
è: I = 180 euro.
a) Scrivete l’equazione del vincolo di bilancio di Aldo e rappresentatelo nel grafico sottostante,
indicando anche le intercette.
2x + 5y = 180; intercette (90, 0) e (0, 36)
y
36
E1
18
45
90
b) Calcolate il saggio marginale di sostituzione tra i due beni.
MRS
x
dU
dx y
dU
x
dy
c) Calcolate il paniere di equilibrio di Aldo e rappresentatelo nel grafico precedente.
2 y
x 45
5 x
y 18
2 x 5 y 180
d) Calcolate la spesa di Aldo per i due beni.
S x 45 * 2 90;
S y 18 * 5 90;
e) Ipotizzando che nel supermercato siano disponibili soltanto 30 yogurt, si rappresenti il nuovo
vincolo di bilancio.
y
36
E2
24
30
x












