MASSIMA UTILITA' DEL CONSUMATORE CON
IL VINCOLO DI BILANCIO
Limitiamo lo studio del problema a un paniere di due soli beni chiamati con x] e X2
Il problema consiste nel massirnizzare l'Utilità del consumatore che per procurarsi i due beni ha a disposizione
una somma B, chiamata nella teoria economica "bilancio".
(il consumatore è colui che acquista beni per destinarli al proprio consumo; L'Utilità è una funzione che
indica il gradimento di un consumatore relativamente alla fruizione di beni e servizi; il panieredi consumo è
l'insieme dei beni che il consumatore acquista)
x] = quantità del primo bene X2 = quantità del secondo bene
La funzione obiettivo è la funzione di utilità U = U(X1 , X2)
con
Xl ≥O
e
X2 ≥O
Il vincolo è costituito dal bilancio B = PIXl + P2X2
La funzione Lagrangiana è :
Per determinare il massimo relativo vincolato utilizziamo la condizione necessaria che consiste nell'
annullare contemporaneamente le derivate parziali prime rispetto a Xl , X2, À
l
U'X1 -p1 =0
U'X2 -p2 =0
P1X1 + P2X2 = B
Si può dimostrare che il sistema ammette una sola soluzione che dal calcolo dell 'Hessiano orlato risulta essere
un massimo relativo e assoluto.
Dalle prime due equazioni del sistema precedente si ricava una importante relazione
U'X1
___
P1
__ =
U'X2
___
=
P2
Questa relazione esprime la seguente proprietà della teoria economica:
Per massimizzare l'Utilità, il consumatore deve distribuire il suo bilancio in modo che sia eguale, per ogni
bene, il rapporto tra l'utilità marginale e il prezzo P del bene.
Il valore di nel punto di massimo viene anche interpretato come utilità marginale della moneta quando sia
massimizzata l'utilità del consumatore
La risoluzione del problema può essere svolta anche geometricamente attraverso lo studio delle linee di livello
della funzione di utilità. .
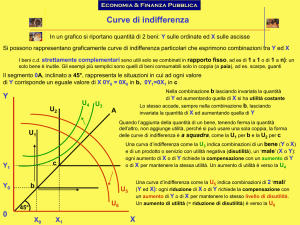
Tali linee di livello vengono chiamate CURVE DI INDIFFERENZA perché ognuna di esse rappresenta tutte
le possibili combinazioni (Xl, X2) delle quantità acquistate dei due beni che lasciano invariata l'Utilità e che
quindi rappresentano consumi indifferenti.
(Ricordiamo alcune caratteristiche delle curve di indifferenza: sono funzioni decrescenti e quindi con pendenza
negativa, la concavità è rivolta verso l'alto, le curve di indifferenza non si intersecano mai tra loro, a curve di
indifferenza più lontane dall 'origine corrispondono livelli di utilità maggiore)
Una possibile rappresentazione delle linee di livello della funzione di Utilità è la seguente
Quando il consumatore acquista dei beni cerca di farlo in modo da rendere il più grande possibile il suo grado di
soddisfazione compatibilmente con il denaro a disposizione.
Il vincolo di bilancio definisce l'insieme dei panieri che il consumatore può acquistare spendendo completamente
il proprio reddito.
Per il consumatore la massima Utilità corrisponde alla scelta del paniere di consumo in corrispondenza del
quale la curva di indifferenza è tangente al vincolo di Bilancio
VINCOLO DI BILANCIO
La rappresentazione grafica del vincolo di bilancio è una retta.
Il coefficiente angolare della retta che rappresenta il vincolo di bilancio è m = - p1/p2
l'ordinata all' origine è
mentre
q = -B/p2
Le variazioni di Bilancio non modificano la pendenza della retta ma ne modificano l'ordinata all'origine (se il
reddito aumenta la retta resta parallela a quella iniziale ma aumenta l'ordinata al! 'origine q;
se viceversa diminuisce il reddito diminuisce l'ordinata al! 'origine q)
La variazione di prezzo di uno dei due beni determina invece una variazione della pendenza della retta
corrispondente al vincolo di bilancio.
Osservando il grafico si può notare che rispetto al punto di massima Utilità ci sono curve di indifferenza che
presentano Utilità maggiore ma il consumatore non ha denaro a sufficienza per accedere ai panieri di tali
curve.