angolo trigonometriche -dalla

Matematica Goniometria e Trigonometria
Domande - esercizi
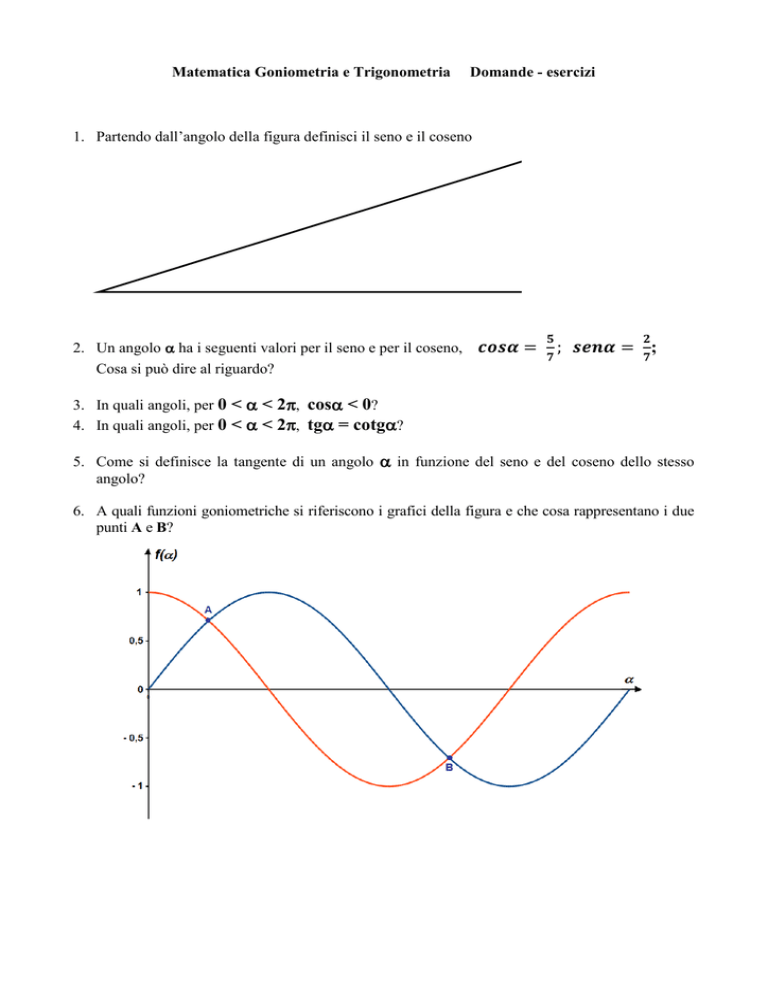
1. Partendo dall’angolo della figura definisci il seno e il coseno
2. Un angolo  ha i seguenti valori per il seno e per il coseno,
Cosa si può dire al riguardo?
;
3. In quali angoli, per 0 <  < 2, cos < 0?
4. In quali angoli, per 0 <  < 2, tg = cotg?
5. Come si definisce la tangente di un angolo  in funzione del seno e del coseno dello stesso
angolo?
6. A quali funzioni goniometriche si riferiscono i grafici della figura e che cosa rappresentano i due
punti A e B?
Matematica Goniometria e Trigonometria
Domande - esercizi
7. A quale funzione goniometrica corrisponde il grafico sottoriportato?
8. Un’equazione goniometrica elementare ha data questo risultato,
; cosa si può
dire in proposito?
9. Un’equazione goniometrica elementare ha data questo risultato, tgx = 5;
plausibile?
è un risultato
2
10. L’equazione 3tg
x+1 = 0, ha soluzioni reali? Spiega la risposta
2
11. Per quali valori di x è soddisfatta la disequazione cos x+1 < 0? Spiega la risposta
12.Con riferimento al triangolo della figura, scrivi sen e sen
13.Con riferimento al triangolo della figura, dire, motivando la risposta, quale relazione esiste tra
cos e sen
Matematica Goniometria e Trigonometria
Domande - esercizi
14. Per quali valori di x, senx > 0 ?
15. Illustra il teorema dei seni, utilizzando il triangolo della figura.
16. Illustra il teorema di Carnot utilizzando il triangolo della figura.
 Stabilire qual è il segno dell’espressione
x

3
(riportare tutti i calcoli) 

18. Risolvere la seguente equazione goniometrica ( usare sen 2 x  cos 2  1 ):
4 sen 2 x  3 cos2 x  4 sen x  0 

19. Risolvere la seguente disequazione goniometrica elementare :

√

, quando
Matematica Goniometria e Trigonometria
Domande - esercizi
20. Calcolare il lato AC del triangolo della figura
C


A
B
AB = 30; CB = 20; 
21.Cosa significa dire che la funzione f(x) = cotgx è periodica di periodo  ?
22. Per un angolo 
√
e
; questi valori sono plausibili? Se la risposta è
si (spiegare la risposta data), determinare il valore dell’angolo 

23. Risolvere la seguente equazione goniometrica:


24. Risolvere la seguente disequazione goniometrica:
√

25. E’ giusto dire che AB = ACcos + CBcosspiega la risposta)
C
A


B
Matematica Goniometria e Trigonometria
Domande - esercizi
26. Calcola l’area del triangolo della figura
AB = 10
 = 60°
 = 70°
(suggerimento: tracciare l’altezza dal vertice C alla
base AB)
, calcolare tg e cotg.
27. Sapendo che


28. Risolvere la seguente equazione goniometrica:
29. Risolvere la seguente equazione goniometrica:
2cosxsen2x - cosx = 0
30. Determinare il lato BC del triangolo sotto riportato
A

B


C
AB = 20;
 
31. Come si definisce la circonferenza goniometrica?
32. Sapendo che
, calcolare tg e cotg.
Matematica Goniometria e Trigonometria
Domande - esercizi
33. Risolvere la seguente equazione goniometrica

34. Risolvere la seguente equazione goniometrica:
2tg2x – 3tgx +1 = 0
35. Come significa che la funzione goniometrica y = sex è limitata?


36. Risolvere la seguente equazione goniometrica:
37. Risolvere la seguente equazione goniometrica:
√
38. Come significa che la funzione y = senx è periodica di 2
39. Risolvere la seguente equazione goniometrica:
40. Risolvere la seguente equazione goniometrica:
2
cosx – 2sen x cosx = 0
41. Per quali angoli, tra 0° e 360°, seno e coseno hanno lo stesso valore?
42. Per quali angoli, tra 0° e 360°, seno e coseno hanno valore opposto?
43. Risolvere la seguente equazione goniometrica (4 punti):
5tg2x – 3tgx  2 = 0
44. Cosa afferma la relazione fondamentale della goniometria e da quale teorema della geometria
razionale deriva?
45. Il teorema di Carnot si può applicare ad un triangolo rettangolo?
46. Risolvi la seguente equazione
44. Risolvi la seguente equazione
(√
√
)
√
Matematica Goniometria e Trigonometria
Domande - esercizi
47. Calcola l’altezza h della montagna rappresentata nella figura sottostante
BC = 3500 m; 33°; 50°;
A

h


B

C
H
48. Determina il valore del lato a e dell’altezza h del triangolo della figura
C= 10 m ; approssima alla prima cifra intera)

c
a
h


b
49.Calcola tg(arctg 3 );
50. Calcola
51. Calcola
sen(arctg
3 );
(
)
52. Qual l’unita di misura del seno di un angolo?
53.Quali sono dominio e codominio della funzione f(x) = tgx
54.Quali sono dominio e codominio della funzione f(x) = cosx