ESAME DI STATO DI LICEO SCIENTIFICO
CORSO DI ORDINAMENTO
Sessione suppletiva 2009
Indirizzo: SCIENTIFICO
QUESITO 4
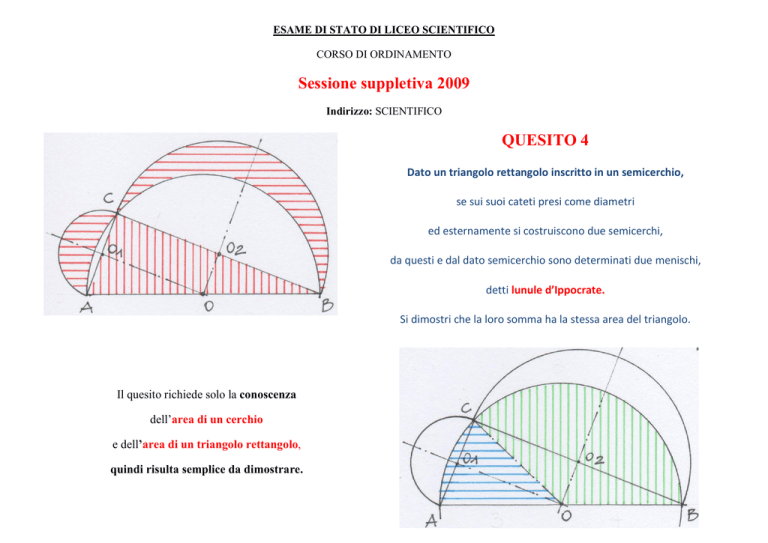
Dato un triangolo rettangolo inscritto in un semicerchio,
se sui suoi cateti presi come diametri
ed esternamente si costruiscono due semicerchi,
da questi e dal dato semicerchio sono determinati due menischi,
detti lunule d’Ippocrate.
Si dimostri che la loro somma ha la stessa area del triangolo.
Il quesito richiede solo la conoscenza
dell’area di un cerchio
e dell’area di un triangolo rettangolo,
quindi risulta semplice da dimostrare.
Le lunule d’Ippocrate
Sono le due regioni piane date dalla differenza tra le superfici dei due
semicerchi ,
aventi come diametri i cateti
e
e
e l’area del semicerchio avente come diametro l’ipotenusa
alla quale è stata sottratta la superficie del triangolo ABC.
Si deve dimostrare che la somma delle aree delle due lunule è uguale all’area del triangolo ABC
+
+
+
vero per il teorema di Pitagora applicato al triangolo ABC.
,
2° modo : dimostrazione trigonometrica
Nel triangolo rettangolo ABC
siano
l’ipotenusa
l’angolo
il cateto
L’area
La somma
e il cateto
.
del triangolo rettangolo ABC è
delle aree delle due lunule è
Si verifica che è uguale all’area
del triangolo rettangolo ABC :
Perché con alcune semplificazioni si ottiene
per il teorema fondamentale della trigonometria.












