SOLUZIONI

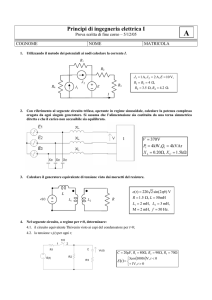
ELETTROTECNICA (10 CFU)
CS INGEGNERIA MATEMATICA
I prova in itinere
20 Novembre 2009
SOLUZIONI
-1-
D1. (punti 4 )
1) Spiegare cosa si intende per DUALITA’ nello studio dei circuiti elettrici.
2) Scrivere per ogni termine della colonna di sinistra il “termine duale” nella colonna
di destra.
Resistore
Resistore
Resistenza
Conduttanza
Induttore
Condensatore
Induttanza
Capacità
Tensione
Corrente
Potenza
Potenza
Serie
Parallelo
Maglia
Nodo (Superficie chiusa)
Thevenin
Norton
Corto circuito
Circuito aperto
La Dualità è una proprietà dei circuiti elettrici per cui definizioni, enunciati, teoremi,
metodi di analisi ecc rimangono validi quando si sostituisce ad ogni termine (quali
quelli sopra elencati) il termine “duale”.
-2-
D2 (punti 4 )
a) Con quali strumenti si misurano la tensione V e la corrente I in un bipolo di un
circuito ?
b) Come si inseriscono nel circuito tali strumenti ?
c) Quale è la differenza tra “strumenti ideali” e “strumenti reali” ?
Risposta: (esempio)
La tensione si misura con il voltmetro (tensiometro) che si collega in parallelo al
bipolo di cui si vuole misurare la tensione.
La corrente si misura con l’amperometro (reometro) che si collega in serie al bipolo
di cui si vuole misurare la corrente.
Il voltmetro ideale è equivalente ad un circuito aperto (G uguale a 0), l’amperometro
ideale è equivalente ad un corto circuito (R uguale a 0).
Il voltmetro reale ha una resistenza R che deve essere grande rispetto alla resistenza
del bipolo di cui si vuole misurare la tensione, l’amperometro reale ha una resistenza
R che deve essere piccola rispetto alla resistenza del bipolo di cui si vuole misurare la
corrente.
-3-
E1 (punti 6) – Regime stazionario
- Calcolare IG
Soluzione
Si consideri C come nodo di riferimento (nodo 0). Si ha eA= 10
KCL in B:
I2 + I3 = 1
(eB – 10) + eB = 1 da cui eB = 5,5V e I3 =- 5,5A
KCL in D:
I1 +2V1 + 1 = 0
(eD – 10) + 2V1 + 1 = 0 ma V1 = 10 - eD quindi
(eD – 10) + 2(10 - eD) + 1 = 0 da cui eD = 11V
IG = - I3 - 2V1 = - 5,5 - 2V1 = - 5,5 – 2(10 – 11) = - 3,5A= - 7/2A
-4-
E2 (punti 8) – Circuiti del I ordine
Gli interruttori sono nella posizione indicata da molto tempo. Per t=0 S1 si porta
(istantaneamente) dalla posizione a alla posizione b e, sempre per t=0 l’interruttore S2
si apre.
Calcolare iL(t) e vL(t) e disegnarne i grafici, mettendo in evidenza i valori per t = 0-,
per t = 0+ e per t che tende all’infinito, nonché la costante di tempo.
Soluzione
Per t < 0 il generatore pilotato è cortocircuitato, il resistore alla sinistra del generatore
indipendente non influenza la parte di destra, per cui il circuito diventa
Quindi iL(0-) = iL(0+) = [15 / (100 + 100||100)] /2 = 0,05A = 50mA
Il termine tra parentesi quadra è la corrente nel generatore che si divide in due parti
uguali. vL(0-) = 0 essendo l’induttore a regime un cortocircuito.
-5-
Dopo la chiusura dell’interruttore il circuito diventa:
Calcolo di iL(∞)
i = 15/100 = 0,15A e quindi 2i = 0,3A
KVL alla maglia indicata:
15 =(iL(∞) + 0,3) 100 + iL(∞) 100 da cui iL(∞) = - 0,075A = - 75mA
vL(∞) = 0 essendo l’induttore a regime un cortocircuito
Calcolo di τ
Per calcolare la R vista dall’induttore si spegne il generatore indipendente di tensione
(cioè diventa un cortocircuito). Quindi i = 0 e il generatore pilotato di corrente 2i,
diventa un circuito aperto
Quindi la R risulta 100 + 100 = 200Ω e τ = L/R = 50nsec
iL(t)= 125e-t/τ-75 mA da cui, derivando e moltiplicando per L si ottiene
vL(∞) = -25e-t/τ da cui vL(0) = 25V
I grafici sono quindi
-6-
E3 (punti 8) – Regime sinusoidale .
vs(t) è un generatore sinusoidale che vale 10 cos(10t) [V]
Is è un generatore costante nel tempo che vale 3 [A]
- Calcolare i(t) a regime
- Calcolare la potenza media dissipata sul resistore da 5 [Ω]
Soluzione.
Poiché ci sono due generatori indipendenti a pulsazioni diverse (ω1 = 10 e ω2 = 0) è
necessario usare la sovrapposizione degli effetti da sommarsi nel dominio del tempo
(NON nel dominio dei fasori).
Con Is spento. (ω = 10)
ZRL = 5 + 15j;
ZRC = 5 - 5j
I’ = Vs/(ZRL + ZRC ) = (1-j)/2 da cui i’(t) = 0.707 cos(10t – 45°)
Con Vs spento (in continua)
I” = - Is 10/(10+5) = - 2 (partitore di corrente)
i(t) = - 2 + 0.707 cos(10t – 45°)
Poiché le pulsazioni sono differenti si sommano le potenze medie; quindi
P’ = ½ R|I’|2 = 5/4W = 1,25W;
P” = R|I”|2 = 20W P= P’+ P”=21,25W
-7-
ELETTROTECNICA (10 CFU)
CS INGEGNERIA MATEMATICA
II prova in itinere
2 Febbraio 2010
SOLUZIONE
-8-
D1. (punti 4 )
Doppio Bipolo 1
Doppio Bipolo 2
Dimostrare quale è il legame tra RS e RT affinchè i due Doppi Bipoli siano
equivalenti (RS e RT sono i valori in Ohm delle resistenze)
----------------------------------------------Soluzione.
La matrice dei parametri Rs del Doppio Bipolo 1 è Rs =
2R S
RS
2
RT
La matrice dei parametri Gt del Doppio Bipolo 2 è Gt =
1
−
RT
I due Doppi Bipoli sono equivalenti se (Rs)-1 = Gt
(Rs)-1 =
1 2R S
2
3R S - R S
- RS
2R S
= Gt
cioè
cioè RT = 3 RS
-9-
RS
2R S
1
RT
2
RT
−
D2. (punti 4 )
Mostrare nei seguenti casi di geometria semplice come i valori della resistenza R,
della capacità C, dell’induttanza L dipendono dai parametri geometrici (lunghezza,
superficie) e dalle proprietà del materiale.
- per R filo cilindrico
- per C armature piane parallele
- per L solenoide con N spire avvolte su un nucleo toroidale
Soluzione:
Il legame costitutivo di un resistore è V = RI ; in un filo di lunghezza L, sezione A e
resistività ρ si ha
V = L E (E = campo elettrico)
I = J A (J = densità di corrente)
E=ρJ
Sostituendo si ottiene R = ρ L/A
Il legame costitutivo di un condensatore è Q = C V ; in un condensatore con
armature piane parallele di area A, poste a distanza d con dielettrico di permettività ε
si ha
V = d E (E = campo elettrico)
Q = D A (D = induzione dielettrica)
D=εE
Sostituendo si ottiene C = ε A/d
Il legame costitutivo di un induttore è Φ = L I ; in un induttore ottenuto da un
solenoide di N spire avvolto su un nucleo toroidale di sezione A, di lunghezze
(media) pari a L con materiale magnetico di permeabilità μ si ha
Φ = NΨ
Ψ = B A (B = induzione magnetica)
NI = H L (H = campo magnetico)
B=μH
Sostituendo si ottiene L =N2 μ A/L
- 10 -
E1 (punti 8) – Circuiti del II ordine
u(t) è un gradino unitario nell’origine.
- Determinare per quale valore di R > 0 il circuito è detto “con smorzamento critico”
- Con il valore di R cosi’ ottenuto, calcolare la corrente nell’induttore iL(t) per t da 0 a
infinito.
-----------------------------------------------------------------------------------Soluzione
Equazioni di stato: (indichiamo con R1 il resistore da 1 Ohm)
& C = − VC − I L + u(t)
CV
R1
R1
L&I L = VC − RI L
−
da cui
A=
Inserendo i valori di R1 C e L si ottiene A =
2α = tr(A) = 1 + R
1
R1C
1
L
1
C
R
−
L
−
−1 −1
1 −R
da cui
e ω02 = R + 1
Il circuito ha smorzamento critico quando le due frequenze naturali sono uguali e cio’
si ha quando α2 = ω02 cioè quando
scartare) e quando R = 3.
1
( R + 1) 2 = R + 1 cioè quando R = -1 (da
4
L’equazione caratteristica è
λ2 + 4λ + 4 = 0 da cui le frequenze naturali coincidenti uguali a -2
- 11 -
La corrente è pertanto
iL(t) = (k1 + k2t) e-2t + iL(∞)
iL(∞) = 1/ (R1 + R) = ¼
iL(0-) = iL(0+) = 0 = k1 + ¼ da cui k1 = - ¼
diL/dt (0) = VC (0) − RI L (0) = 0 = k2 + k1 (-2) da cui k2 = -1/2
Quindi iL(t) = - (1/4 + 1/2t) e-2t + 1/4
- 12 -
ELETTROTECNICA (10 CFU)
CS INGEGNERIA MATEMATICA
Prova scritta
23 Febbraio 2010
SOLUZIONE
- 13 -
E1 (punti 7) – Regime stazionario
-------------------------------------------------------------------------------------------------Soluzione.
KCL al nodo 2:
(e2-e1) + e2 + (e2-e3) = 12
(1)
KCL al supernodo 1-3
e1 + (e1 – e2) + (e3 – e2) + e3 + 12 = 0
(2)
Vincolo del generatore pilotato
(e3 – e1) = 1 e1
(3)
Da cui:
e1 = - 1V;
e2 = 3V;
e3 = -2V
IG = - (e1/R) – 12 + (e2 – e1)/R = +1 – 12 + 4 = -7 A
P = IG*e1 = (-7)*(-1) = 7 Watt
- 14 -
E2 (punti 7) – OP-AMP in regime sinusoidale
R1 = R2 = 10 kΩ
C = 0.1 nF
vs(t) = 20 cos(104 t)
R = 100 Ω
L = 10 mH
- Calcolare la funzione di rete H(jω) = V0/Vs
- Determinare v0(t)
- Collegare il bipolo RL (A con A’, B con B’) e calcolare la potenza attiva P e la
potenza reattiva Q sul bipolo A’ B’
----------------------------------------------------------------------------------------------Soluzione.
Il fasore della corrente uscente dal generatore vale Vs/R1 e la stessa corrente entra nel
bipolo CR2 la tensione al capi del quale è V0 cambiata di segno. Si ha quindi:
V0 = −
VS
1
1
1
= −VS
da cui H(jω ) = −
-6
R 1 (G 2 + jωC)
(1 + jω10 )
(1 + jω10 -6 )
H(j10-4) ≈ -1 e v0(t) = -20 cos(104 t) = 20 cos(104 t + π)
1
1VV 1
400
A= VI=
=
= 1+ j
2
2 Z
2 100 − j100
da cui P = 1W e Q = 1VAR
- 15 -
E3 (punti 8) – Circuiti del II ordine
R1 = 1Ω; R2 = 16/3 Ω ; R3 = 2Ω ; C = 1F ; L = 1H ; μ= ½
vs(t) = 35u(t) [gradino in t = 0 di ampiezza 35 Volt]
Calcolare iL(t) per t da 0 a infinito e tracciarne il grafico.
---------------------------------------------------------------------------------------------Soluzione
Equazioni di stato (VC = V ; IL = I)
& =−
CV
V −V
V
V
+I+ S
−μ
R3
R1
R1
L&I = −R 2 I − V + VS
−2
+1
16
Inserendo i valori di R1 R2 R3 C μ e L si ottiene A =
−1 −
3
2α = - tr(A) = 22/3
e ω02 = 35/3
L’equazione caratteristica è
λ2 +
22
35
λ + = 0 da cui le frequenze naturali λ1 = -5 e λ2 = -7/3
3
3
La corrente è pertanto iL(t) = k1e-5t + k2e-7/3t + iL(∞)
iL(∞) = 9/2
iL(0-) = iL(0+) = 0 = k1 + k2 + 9/2
diL/dt (0) = 35 = k1 (-5) + k2 (-7/3)
da cui k1 = -147/16 e k2 = 75/16
- 16 -
da cui
E4 (punti 6) – Circuiti magnetici
μ0 = 12,5 10-7 H/m
μr1 = 4000
μr2 = 8000
S = 0,5 cm2
l = 3 cm
t = 0,1 mm
Determinare N in modo che ai morsetti si abbia una induttanza di circa 60 mH
Soluzione
La riluttanza dei tratti di lunghezza l di materiale 1 vale R1 = l / μ0μr1 S = 1,2 105
La riluttanza del tratto di lunghezza l di materiale 2 vale R2 = l / μ0μr2 S = 0,6 105
La riluttanza del traferro vale Rt = t / μ0 S = 16 105
La riluttanza R vista dall’avvolgimento vale
R = 3 R1 + R2||(Rt + 3 R1) ≈ 3 R1 + R2||Rt ≈ 3 R1 + R2 = 4,2 105
L = N2/Rt = 60 mH da cui N = 158,74 quindi 159 spire.
- 17 -
ELETTROTECNICA (10 CFU)
CS INGEGNERIA MATEMATICA
Prova scritta
7 Luglio 2010
SOLUZIONE
- 18 -
E1 (punti 7) – Regime stazionario
Calcolare la corrente I :
a) usando il metodo dell’analisi nodale
b) applicando il Teorema di Thevenin ai morsetti A B
- 19 -
- 20 -
E2 (punti 7) – Bipoli equivalenti in regime sinusoidale
Determinare il bipolo equivalente Thevenin ai morsetti AB calcolando Zth e Vth
Soluzione
- 21 -
E3 (punti 8) – Circuiti del II ordine
Calcolare v1(t) da 0 all’infinito e tracciarne il grafico.
Soluzione
- 22 -
E4 (punti 6) – Doppi bipoli
a) Calcolare la matrice dei parametri R
b) Disegnare lo schema circuitale di un doppio bipolo equivalente (con la stessa
matrice R) comprendente solo resistori
Soluzione
- 23 -
CS INGEGNERIA MATEMATICA
ELETTROTECNICA (10 CFU)
Prova scritta
9 Settembre 2010
SOLUZIONE
- 24 -
E1 (punti 7) – Regime stazionario
Calcolare la corrente I
Soluzione
- 25 -
E2 (punti 7) –Regime sinusoidale
Calcolare v(t) a regime con il metodo dei fasori.
Soluzione
- 26 -
E3 (punti 8) – Circuiti del II ordine (Transitorio)
vs(t) è un gradino unitario nell’origine
Calcolare v(t) per t da 0 a infinito.
Disegnare il grafico di v(t)
Suggerimento: esprimere v(t) in funzione delle variabili di stato
Soluzione
- 27 -
E4 (punti 6) – Circuiti magnetici
Il circuito magnetico ha permeabilità μFE = ∞; sono note le dimensioni geometriche;
non c’è flusso disperso; il traferro t è in aria (permeabilità μ0)
Calcolare la matrice delle induttanze L della struttura magnetica mostrata in figura.
Soluzione
- 28 -
CS INGEGNERIA MATEMATICA
ELETTROTECNICA (10 CFU)
Prova scritta
24 Settembre 2010
SOLUZIONE
- 29 -
E1 (punti 6) – Regime stazionario
Determinare per quale valore di Is la corrente I vale 4 A. Calcolare in tale condizione
le potenze erogate dai due generatori indipendenti.
Soluzione
V = 4·10 = 40 Volt
V1 = 50 – 40 = 10 Volt
I1 = 10/5 = 2 Ampère
I2 = V/40 = 1 Ampère
IS = I + I2 – I1 = 3 Ampère
PIs = 3·40 = 120 Watt
PVs = 50·2 = 100 Watt
- 30 -
E2 (punti 7) – Regime sinusoidale
Il circuito in figura ha due generatori indipendenti, un generatore di tensione costante
(E = 5 Volt) e un generatore di corrente sinusoidale ( Is(t) = 2 sin(5t) ).
Calcolare v(t) a regime.
Soluzione
- 31 -
E3 (punti 8) – Circuiti del II ordine (Transitorio)
Calcolare i1(t) da 0 all’infinito
Tracciare il grafico di i1(t)
Soluzione
- 32 -
E4 (punti 7) – Doppi bipoli
Calcolare i parametri conduttanza G (ammettenza Y) del doppio bipolo seguente:
Soluzione.
Poiché il Doppio Bipolo ha una struttura a T è conveniente calcolare i parametri R
(resistenza) e quindi invertire la matrice.
- 33 -
E2 (punti 8) – Doppi Bipoli
Calcolare, tra le matrici cardinali R, G, H, H’, quelle che esistono.
L’OP-AMP è ideale.
Soluzione.
R1
R
R=
− R 4 (1 + 2 ) + R 2
R3
0
dato che det(R) = 0 la matrice G non esiste
0
1
R1
la seconda matrice ibrida H′ =
−
0
⎤
1 ⎡
R2
R
(1
)
R
0
+
+
2⎥
4
R 1 ⎢⎣
R3
⎦
Dato che det(H’) = 0 la matrice dei parametri H non esiste.
- 34 -
E3 (punti 8) – Circuiti magnetici
Il circuito magnetico ha permeabilità μFE = ∞; sono note le dimensioni geometriche;
non c’è flusso disperso; il traferro t è in aria (permeabilità μ0)
a) Calcolare i parametri L1, L2 e M degli induttori mutuamente accoppiati ai
morsetti AA’ e BB’
b) Collegare il morsetto A’ con B e calcolare l’induttanza L che si vede ai
morsetti A B’
---------------------------------------------------------------------------Soluzione
Indicato con Rt la riluttanza del traferro = t/A μ0
2
N1
Rt
L=
N1 N 2
Rt
N1 N 2
Rt
2 2
N2
Rt
Essendo i due avvolgimenti collegati in serie l’induttanza ai morsetti A B’ vale
L1 + L2 + 2M = (N12 + 2N1N2 + 2 N22 )/ Rt
- 35 -