ELETTROTECNICA (10 CFU)
CS INGEGNERIA MATEMATICA
Prova scritta
7 Settembre 2012
SOLUZIONE
E1 (punti 6) – Regime stazionario
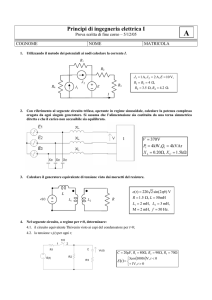
Determinare l’equivalente Thevenin ai morsetti AB
Soluzione
La tensione sul resistore da 4Ω vale Vx.
a) Calcolo della tensione a vuoto Vt = Vx
KCL alla superficie tratteggiata: 5 + Vx/4 – Vx/6 = 0 -> Vx = - 60V = Vt
b) Calcolo di Rt
KCL al nodo B : Vx/4 – Vx/6 + 1 = 0 -> Vx = - 12
Rt = V/1 = Vx+ 2 ·(1) = -10 Ω = Rt
E2 (punti 6) – Regime sinusoidale
a(t) è un generatore di corrente costante nel tempo = 14A
e(t) è un generatore di tensione sinusoidale = 110 cos(20t)
- Calcolare la corrente i(t) a regime
- Calcolare la potenza media assorbita dal resistore R = 2Ω
Soluzione
Poiché ci sono due generatori a pulsazioni diverse (a(t) con ω = 0 e e(t) con ω = 20) si
deve usate la sovrapposizione degli effetti nel dominio del tempo.
a) Con a(t) acceso e e(t) spento, a ω = 0 (cioè in continua) il circuito diventa:
La corrente i(t) vale (partitore di corrente) i = 14·(12/14) = 12A
b) Con a(t) spento e e(t) acceso, a ω = 20 (cioè in continua) il circuito diventa, in
termini di fasori:
ZL = jωL = j 4
YC = jωC = j 0,2
L’ammettenza della parte tratteggiata YT = 1/(R+ZL) + YC = 1/(2+4j) + j 0,2 = 0,1S
da cui ZT = 10Ω.
La corrente erogata dal generatore vale quindi IG = 110/(12+10) = 5A
La corrente nel resistore R si ottiene con il partitore di corrente:
IR =IG · ZC/(ZC + R + ZL) = 5 · (-j5)/(-j5+2+j4) = 5(1-2j)
Trasformo il fasore IR in sinusoide iR(t) = 5√5 cos(20t – 63°)
Sommo ora i due contributi trovati: la corrente i(t) = 12 + 5√5 cos(20t – 63°)
Poiché i due generatori sono a frequenze diverse la potenza media si ottiene
sommando le potenze medie dei due generatori calcolati separatamente (sommabilità
delle potenze medie).
Per ω = 0 la potenza è RI2 = 2·12·12 = 288W.
Per ω = 20 la potenza media è ½ ·R·|IR|2 = ½ ·2·|25·5| = 125W
La potenza media con i due generatori accessi è quindi 288 + 125 = 413W
E3 (punti 6) – Circuiti del II ordine
- Determinare per quale valore di K il circuito è senza smorzamento.
- Per tale valore di K calcolare v1(t) e v2(t) da 0 a ∞ con condizioni iniziali
v1(0) = 10V e v2(0) = 0.
Soluzione.
IC2 = - (V1 + V2) + KV1
IC1 = IC2 - V1 = - (V1 + V2) + KV1 – V1
Le equazioni di stato sono
2
1
da cui la matrice A =
2
1
1
1
Il polinomio caratteristico è quindi χ(λ) = λ2 + (3 – K)λ + 1 = 0
Il circuito è senza smorzamento (due frequenze naturali immaginarie pure) per K = 3.
Le frequenze naturali sono λ1 e λ2 = ±j
v1(t) = A cos(t) + B sen(t)
Imponendo le condizioni iniziali v1(0)=10 (dato) e
si ottiene v1(t) = 10 cos(t) + 10 sen(t)
Analogamente:
v2(t) = C cos(t) + D sen(t)
Imponendo le condizioni iniziali v2(0)=0 (dato) e
si ottiene v2(t) = 20 sen(t)
10 (dalle equazioni di stato)
20 (dalle equazioni di stato)
E4 (punti 6) Circuiti magnetici
La struttura mostrata in figura è realizzata con un materiale di permeabilità µ
Dati:
µ = 10-3H/m ; N1 = 150; N2 = 300; N3 = 100; l = 40cm, S = 4cm2
I1 = 2A; I2 = 1A; I3 = 5A
- Calcolare il flusso ψ3
Soluzione
La riluttanza di ogni tronco è R = l/µS = 106 .
Si nota inoltre che le due f.m.m. N1I1 = 300 = N2I2 sono uguali ma di segno opposto e
quindi si annullano.
Costruisco il circuito analogo elettrico.
ψ3 = N3I3/(2,5R) = 2·10-4 Tm2