FASCIO DI RETTE
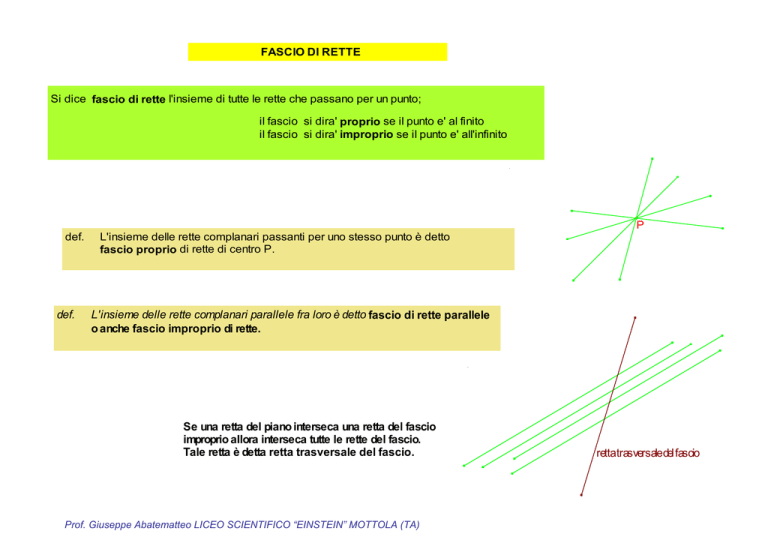
Si dice fascio di rette l'insieme di tutte le rette che passano per un punto;
il fascio si dira' proprio se il punto e' al finito
il fascio si dira' improprio se il punto e' all'infinito
P
def.
def.
L'insieme delle rette complanari passanti per uno stesso punto è detto
fascio proprio di rette di centro P.
L'insieme delle rette complanari parallele fra loro è detto fascio di rette parallele
o anche fascio improprio di rette.
Se una retta del piano interseca una retta del fascio
improprio allora interseca tutte le rette del fascio.
Tale retta è detta retta trasversale del fascio.
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
rettatrasversaledel fascio
t
A
r1
r2
B
r3
r4
C
D
r5
t'
A'
B'
C'
D'
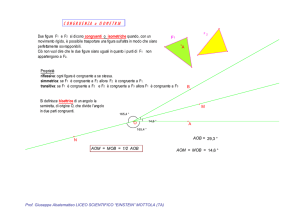
La corrispondenza di Talete: Si consideri un fascio improprio e siano t e
t' due rette trasversali del fascio.
Tali rette intersecano ciascuna retta del fascio in due punti che si dicono
fra loro corrispondenti; inoltre ad ogni coppia di rette del fascio
corrispondono due segmenti, relativi alle due trasversali.
cioè: A e A' come B e B' ecc. sono punti corrispondenti;
AB e A'B' ecc. sono segmenti corrispondenti.
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
t
T
Se un fascio improprio è tagliato da due trasversali
allora a segmenti congruenti dell'una corrispondono
segmenti congruenti dell'altra.
ipotesi
se AB = CD
tesi
allora A'B' = C'D'
dimostraz.
Si conducano da A e C le // alla retta t'.
I triangoli APB e CQD sono congruenti in quanto hanno un
lato e gli angoli adiacenti rispettivamente isometrici fra loro.
Quindi AP =CQ e di conseguenza A'B' = C'D'
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
r1
A
r2
B
r3
r3
t'
C
A'
P
B'
C'
D
D'
Q
A
COROLLARIO
Si consideri il triangolo ABC, si tracci per
il punto medio di un lato la // ad un altro
lato. Il terzo lato sarà intersecato dalla //
proprio nel suo punto medio.
ipotesi
se r // BC e passante per M
M'
M
r
tesi
allora AM' = M'C
-►
C
B
A
T
Sia ABC un triangolo qualunque.
Il segmento che congiunge i punti medi di due qualsiasi lati del
triangolo,
risulta // al terzo lato e congreuente alla sua metà.
ipotesi
se A M1 = M1 B
A M2 = M2 C
tesi
allora M1 M2 // BC
M1 M2 = 1/2 BC
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
M2
M1
B
M3
C
APPLICAZIONI problemi.
Sia AB un segmento che lo si vuol dividere in un numero di n parti comgruenti fra loro.
1°- Dall'estremo A si tracci un segmento qualsiasi, inclinato di un qualsiasi angolo rispetto ad AB, e su questo si stacchino n segmenti
congruenti fra loro di qualsiasi lunghezza.
2°- Si congiunga l'ultimo estremo degli n segmenti con l'estrem B e parallelamente a questo si traccino i segmenti a partire dai singoli
estremi.
Queste parallele divideranno anche il segmento AB in n parti congruenti fra loro
P
3
problema N.1
Sia AB un segmento lungo ad es.10 cm e lo si vuole dividere
in tre parti congruenti fra loro.
P2
P1
4,00 cm
A
problema N.2
Sia ABC un triangolo isoscele.
Dimostrtare che la perpendicolare alla base condotta dal punto medio di uno
degli altri lati, divide la base stessa in due segmenti uno il triplio dell'altro.
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
10,00 cm
B