C O N G R U E N Z A o IS O M E T R IA
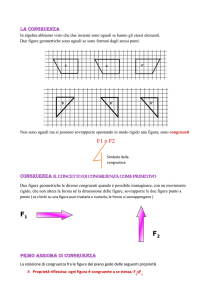
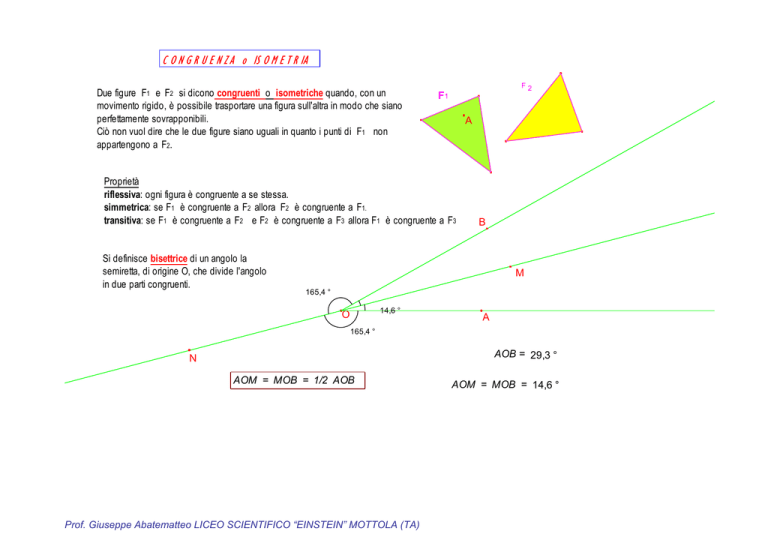
Due figure F1 e F2 si dicono congruenti o isometriche quando, con un
movimento rigido, è possibile trasportare una figura sull'altra in modo che siano
perfettamente sovrapponibili.
Ciò non vuol dire che le due figure siano uguali in quanto i punti di F1 non
appartengono a F2.
F2
F1
A
Proprietà
riflessiva: ogni figura è congruente a se stessa.
simmetrica: se F1 è congruente a F2 allora F2 è congruente a F1.
transitiva: se F1 è congruente a F2 e F2 è congruente a F3 allora F1 è congruente a F3
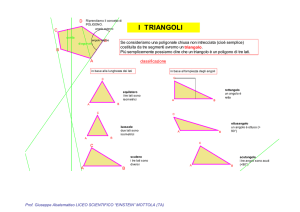
Si definisce bisettrice di un angolo la
semiretta, di origine O, che divide l'angolo
in due parti congruenti.
B
M
165,4 °
14,6 °
O
A
165,4 °
AOB = 29,3 °
N
AOM = MOB = 1/2 AOB
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
AOM = MOB = 14,6 °
S IM M E T R IA R IS P E T T O A D U N P U N T O :
A1
D i re m o c h e d u e p u n ti A e B s o n o s i m m e tri c i ri s p e tto a d u n
a l tro p u n to
M , q u a n d o M è i l p u n to m e d i o d e l s e g m e n to A B .
B1
F1
F2
C1
C o n s i d e ri a m o l e fi g u re F 1 e F 2 , e s s e s o n o s i m m e tri c h e ri s p e tto a l
M
p u n to M i n q u a n to M è i l p u n to m e d i o d i o g n i s g m e n to c h e h a p e r
e s tre m i d u e p u n ti s i m m e tri c i . M è d e tto c e n t r o d i s i m m e t r i a .
C2
F2
B2
A2
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
A1
B
S IM M E T R IA R IS P E T T O A D U N A R E T T A :
D i re m o c h e d u e p u n ti A e B s o n o s i m m e tri c i ri s p e tto a d
u n a re tta r s e q u e s ta è a s s e ri s p e tto a l s e g m e n to A B .
F1
H
In fa tti l ' a s s e d i u n s e g m e n t o A B è l a re tta p e rp e n d i c o l a re
B1
r
p a s s a n te p e r i l p u n to m e d i o d e l s e g m e n to A B .
B2
A
90,0 °
Consideriamo due figure F1 e F2, esse sono simmetriche rispetto
ad una retta r se i punti di F1 sono i simmetrici rispetto ad r dei
punti di F2. La retta r è detta asse di simmetria.
F2
A2
Il p u n tp H è d e tto p i e d e d e l l a p e r p e n d i c o l a r e e ra p p re s e n ta
l a p r o i e z i o n e o r t o g o n a l e d e l p u n to s u l l a re tta r.
quindi due figure simmetriche sono congruenti
C
A
di conseguenza, ad es. gli angoli opposti al vertice sono congruenti, infatti
il vertice O rappresenta il centro di simmetria dei due settori angolari.
39,0 °
O
39,0 °
D
B
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
MISURA DI SEGMENTI
DI ANGOLI
DI SUPERFICI
B
A
S e g m e n t i c o n g r u e n ti h a n n o l a s te s s a l u n g h e z z a .
M i s u r a r e u n s e g m e n to A B v u o l d i r e c o n fr o n ta r l o c o n u n
a l tr o s e g m e n to u , s c e l to c o m e u n i tà d i m i s u r a ;
a vre m o q u in d i
AB
= n u
unità di misura: metro lineare (m)
analogamente
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
u
n =7
AB = 7u
A
Angoli congruenti hanno la stessa ampiezza.
Misurare un angolo AOB vuol dire confrontarlo con un
altro angolo U, scelto come unità di misura;
avremo quindi AOB = n U
unità di misura: grado (°) opp. radianti (rad)
Ricordiamo che la circonferenza goniometrica è suddivisa in 360°,
che 1°= 60' (60 primi) e
che 1' = 60"(60 secondi)
pertanto, ad es. 42,54° equivale a 42°32'24 "
infatti possiamo scrivere che 42,54° = 42°+ (0,54x 60)'
quindi (0,54 x 60)'= 32,4' che equivale a 32'+ (0,4x 60)"
quindi (0,4 x 60)"= 24"
viceversa
per passare da secondi in primi e da primi in gradi gisogna dividere
per 60.
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
O
B
U
S
Superfici congruenti hanno la stessa area.
Misurare una superficie S vuol dire confrontarla con
un'altra superficie U, scelta come unità di misura;
avremo quindi S = n U
U
U
unità di misura: metro quadrato (m2)
n =3 2
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
S = 32 U